Solved Example Problems [Current and Voltage Division Principle]

VOLTAGE DIVISION PRINCIPLE

Example: 3

Two resistors 15 Ω and 30 Ω connected in series. Find the equivalent resistance.

Req = R1 + R2

= 15+ 30

= 45Ω

Example: 4

Two resistors 5 Ω and 5 Ω connected in parallel. Find the equivalent resistance.

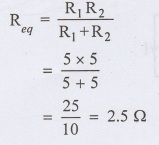
Example: 5

Find the equivalent resistance between A & B 

Example: 6

Two resistors connected in parallel across 200 V supply take 10 A from the mains. If the power dissipated in one resistor is 800 W. Find the value of the other resistor.

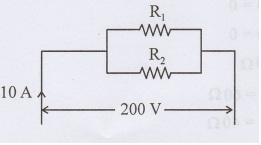
Total power taken P = V x I = 200 × 10 = 200 W

Power dissipated in one resistor P1 = 800 W

Power dissipated in the other resistor P2 = P − P1 = 2000 - 800 =1200 W

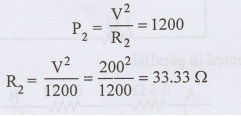
Example: 7

The effective resistance of two resistors connected in series is 100 Ω when connected in parallel the effective value is 24 Ω. Determine the values of the two resistors.

Let the two resistors R1 and R2

When the resistors connected in series

R1 +R2 = 100

R2 = 100 - R1

When in parallel

R1R2 / R1+R2 = 24

R1R2 / 100 = 24

R1 (100 - R1) = 24 × 100

100R1 - R12 = 2400

R12- 100R1 +2400 = 0

(R1 -60) (R1 -40) = 0

R1 = 40 Ω (or) 60 Ω

If  R1 = 40 Ω and R2 =60 Ω

R1 = 60 Ω and R2 = 40 Ω

Example: 8

Find the current in 4 Ω resistor.

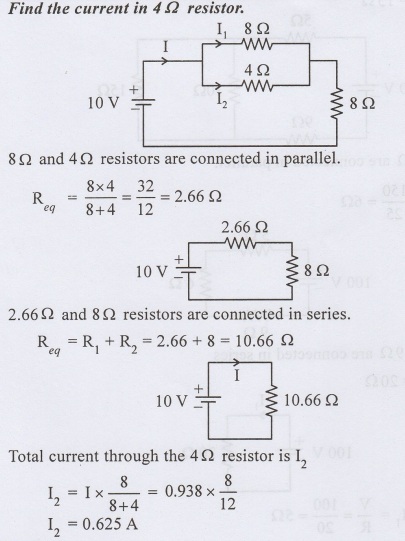
For the circuit shown in fig. calculate equivalent resistances of circuit and total circuit current.

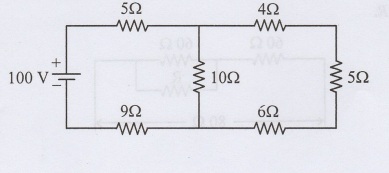
4 Ω, 5 Ω, 6 Ω are connected in series.

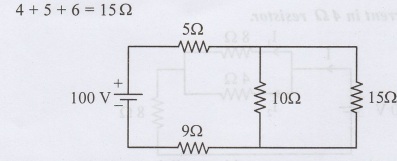
10 Ω and 15 Ω are connected in parallel.

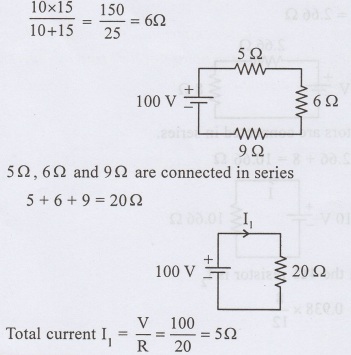
Example: 10

Two 60 Ω resistors are connected in series. If a resistor R is connected across one of them, the total circuit resistance becomes 80 Ω. Find the value of R.

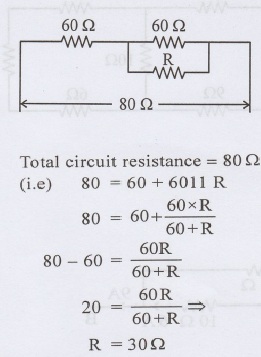
R = 30A

Example: 11

Determine the effective resistance between terminals A and B in the circuit shown in figure. If the current drawn at point A is 9 A, find the current and the voltage drop across each element.

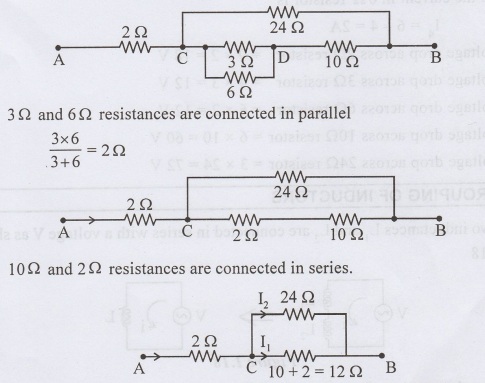
The current at point C splits into two parts one along the 12 Ω resistor (I1) and the other along the 24 Ω resistor (I2). The current I1 and I2 can be found from current division rule.

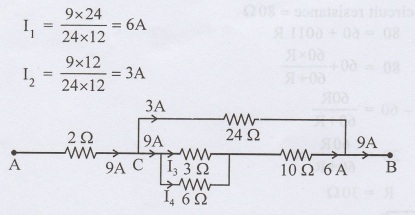
From the point C, 6A current splits into 2 parts and the current through the 3 Ω resistor is 13.

I₃ = 6×6 / 6+3 = 36/9 = 4A

So the current in 6 Ω resistor is

I4 = 6 - 4 = 2A

Voltage drop across 2 Ω resistor = 9 x 2 = 18 V

Voltage drop across 3 Ω resistor = 4 × 3 = 12 V

Voltage drop across 6 Ω resistor = 6 x 2 = 12 V

Voltage drop across 10 Ω resistor = 6 x 10 = 60 V

Voltage drop across 24 Ω resistor = 3 x 24 = 72 V