Perceptron

UNIT V

Chapter: 10: Neural Networks

Syllabus

Perceptron - Multilayer perceptron, activation functions, network training - gradient descent Se optimization - stochastic gradient descent, error backpropagation, from shallow networks to deep networks -Unit saturation (aka the vanishing gradient problem) - ReLU, hyperparameter tuning, batch normalization, regularization, dropout.

Perceptron

• The perceptron is a feed-forward network with one output neuron that learns a separating hyper-plane in a pattern space.

• The "n" linear Fx neurons feed forward to one threshold output Fy neuron. The perceptron separates linearly separable set of pa set of patterns.

Single Layer Perceptron

• The perceptron is a feed-forward network with one output neuron that learns a separating hyper-plane in a pattern space. The "n" linear Fx neurons feed forward to one threshold output Fy neuron. The perceptron separates linearly separable set of patterns.

• SLP is the simplest type of artificial neural networks and can only classify linearly inseparable cases with a binary target (1, 0).

• We can connect any number of McCulloch-Pitts neurons together in any way we like. An arrangement of one input layer of McCulloch-Pitts neurons feeding forward to one output layer of McCulloch-Pitts neurons is known as a Perceptron.

• A single layer feed-forward network consists of one or more output neurons, each of which is connected with a weighting factor Wij to all of the inputs X_i.

• The Perceptron is a kind of a single-layer artificial network with only one neuron. The Percepton is a network in which the neuron unit calculates the linear combination of its real-valued or boolean inputs and passes it through a threshold activation function. Fig. 10.1.1 shows Perceptron.

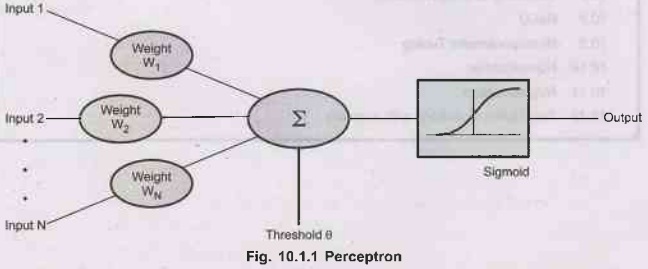
• The Perceptron is sometimes referred to a Threshold Logic Unit (TLU) since it discriminates the data depending on whether the sum is greater than the threshold value.

• In the simplest case the network has only two inputs and a single output. The output of the neuron is:

y = f ( Σ²_i=1 W_iX_i + b)

• Suppose that the activation function is a threshold then

f = {1    if s > 0

       -1   if s < 0

• The Perceptron can represent most of the primitive boolean functions: AND, OR, NAND and NOR but can not represent XOR.

• In single layer perceptron, initial weight values are assigned randomly because it does not have previous knowledge. It sum all the weighted inputs. If the sum is greater than the threshold value then it is activated i.e. output = 1.

Output

W₁X₁ + W₂X₂ +...+ W_nX_n > 0 ⇒ 1

W₁X₁ + W₂X₂ +...+ W_nX_n ≤ 0 ⇒ 0

• The input values are presented to the perceptron, and if the predicted output is the same as the desired output, then the performance is considered satisfactory and no changes to the weights are made.

• If the output does not match the desired output, then the weights need to be changed to reduce the error.

• The weight adjustment is done as follows:

 ∆W = ῃ × d × x

Where

x = Input data

d = Predicted output and desired output.

ῃ = Learning rate

• If the output of the perceptron is correct then we do not take any action. If the output is incorrect then the weight vector is W→ W + W.

• The process of weight adaptation is called learning.

• Perceptron Learning Algorithm:

1. Select random sample from training set as input.

2. If classification is correct, do nothing.

3. If classification is incorrect, modify the weight vector W using

W_i = W_i + ῃd (n) X_i (n)

Repeat this procedure until the entire training set is classified correctly.

Multilayer Perceptron

• A multi-layer perceptron (MLP) has the same structure of a single layer perceptron with one or more hidden layers. An MLP is a network of simple neurons called perceptrons.

• A typical multilayer perceptron network consists of a set of source nodes forming the input layer, one or more hidden layers of computation nodes, and an output layer of nodes.

• It is not possible to find weights which enable single layer perceptrons to deal with non-linearly separable problems like XOR: See Fig. 10.1.2.

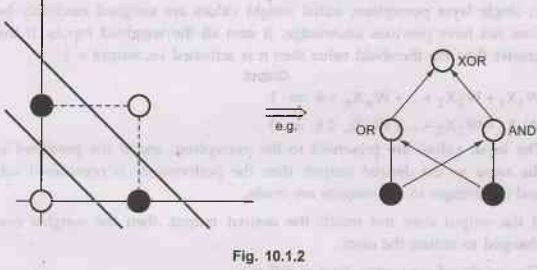
Limitation of Learning in Perceptron: linear separability

• Consider two-input patterns (X₁, X₂) being classified into two classes as shown in Fig. 10.1.3. Each point with either symbol of x or 0 represents a pattern with a set of values (X₁, X₂).

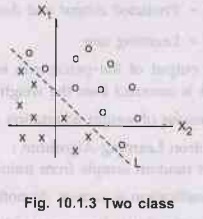
• Each pattern is classified into one of two classes. Notice that these classes can be separated with a single line L. They are known as linearly separable patterns.

• Linear separability refers to the fact that classes of patterns with n-dimensional vector x = (x₁, x₂, …x_n) can be separated with a single decision surface. In the case above, the line L represents the decision surface.

• If two classes of patterns can be separated by a decision boundary, represented by the linear equation then they are said to be linearly separable. The simple network can correctly classify any patterns.

• Decision boundary (i.e., W, b or q) of linearly separable classes can be determined either by some learning procedures or by solving linear equation systems based on representative patterns of each classes.

• If such a decision boundary does not exist, then the two classes are said to be linearly inseparable.

• Linearly inseparable problems cannot be solved by the simple network, more sophisticated architecture is needed.

• Examples of linearly separable classes

• 1. Logical AND function

 2. Logical OR function

• Examples of linearly inseparable classes

1. Logical XOR (exclusive OR) function

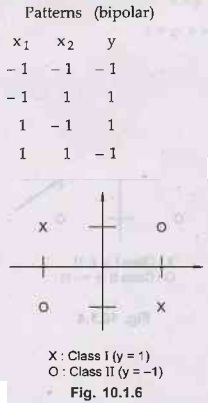
No line can separate these two classes, as can be seen from the fact that the following linear inequality system has no solution.

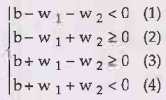
because we have b < 0 from (1) +(4), and b >= 0 from (2) + (3), which is a contradiction.