Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits
Mesh Analysis
Steps, Example Figure with Equation | Electrical Circuits
Mesh and nodal analysis are the two basic techniques used to find solutions for a network.
MESH ANALYSIS
Mesh and nodal analysis are the two basic techniques used to find solutions for a network. The suitability of either mesh or nodal analysis to a particular problem mainly depends on the number of voltage sources or current sources. If a network has a large number of voltage sources, it is useful to use mesh analysis. If any current source in a circuit they converted into equivalent voltage source. If the network has more current sources, nodal analysis is more useful.
A Mesh is defined as a loop which does not contain any other loops within it. Consider a simple network as shown in fig 1.23
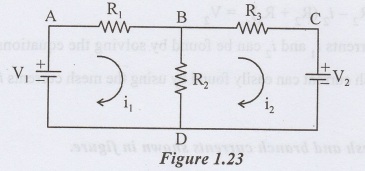
Steps to be followed to find out the mesh current and branch current are
Step 1: Each mesh is assigned a seperate mesh current. Assume all mesh currents directions are clockwise. Consider fig 1.23, it consists of two meshes (ABDA and BCDB) and two mesh currents (i1 and i2).
Step 2: If two mesh currents (i1 and i2) are flowing through a network element, the actual current in the circuit element is the algebraic sum of the two (i1 and i2). In the above network mesh currents i1 and i2 are flowing in R2. First consider the direction B to D, current is i1 –i2 and consider the direction D to B. current is i2 – i1.
Step 3: Write equation for each mesh in terms of mesh currents by applying KVL. In this equation potential rise is mentioned as positive sign (+) and potential drop as negative sign (-).
Step 4: If any one mesh current becomes negative the actual or true direction of the current is anticlockwise.
We apply KVL to the fig 1.23
Mesh ABDA
− i1 R1 − (i1 – i2) R2 + V1 = 0
− i1 R1 − i1 R2 + i2 R2 + V1 = 0
− i1 ( R1 + R2 ) – i2 R2 + V1 = 0
i1 ( R1 + R2 ) – i2 R2 = V1
Mesh BCDB
− i2 R3 − V2 − ( i2 − i1 ) R2 = 0
− i2 R3 − V2 − i2 R2 − i1 R2 = 0
i1 R2 − i2 (R2 + R3) = V2
The mesh currents i1 and i2 can be found by solving the equations V1 and V2.
Step 5: The branch current can easily found by using the mesh currents i1 and i2.
Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits : Tag: : Steps, Example Figure with Equation | Electrical Circuits - Mesh Analysis
Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits
Under Subject
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation