Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits
Solved Example Problems [Mesh Analysis]
Electrical Circuits
Mesh and nodal analysis are the two basic techniques used to find solutions for a network.
MESH ANALYSIS
Example: 23
Solve the mesh and branch currents shown in figure.

First assign mesh (or) loop currents to the two meshes (ABCA and BDCB) as i1 and i2. Assume the current directions as clockwise mesh ABCA
- 30i1 - 10(i1 - į2) + 120 = 0
-30i1 – 10 i1 + 10 i2 + 120 = 0
-40 i1 + 10 i2+ 120 = 0
120 = 40 i1 – 10 i2 …………(1)
Mesh BDCB
-50i2- 60 - 10(i2 – i1) = 0
-50i2 -10 i2 + 10 i1 - 60 = 0
-60 i2 + 10 i1 − 60 = 0
-60 = -10 i1 + 60 i2 …………..(2)
Multiplying equ (2) by 4 and adding the equ (2) in to equ (1)
120 = 40i1 - 10i2
-240= -40i1 +240i2
________________
-120 = 230i2
i2 = -120/230 = -0.521 A
The negative sign indicates that the direction of i2 is anticlockwise.
The i, value is substituted in equ (1)
40 i1 - 10 (-0.521) = 120
40 i1 + 5.21 = 120
40 i1 = 114.79
i1 = 114.79/40 = 2869 A

The actual direction of flow of mesh currents is shown in above fig
The mesh currents i1 = 2.869 A
i2 = 0.521 A
Current in branch CAB is
i1 = 2.869 A
Current in branch CDB is
i2 = 0.521 A
Current in branch BC is = i1 + i2
= 2.869 +0.521
= 3.39 A
Example : 24
Determine the voltage across the 3 Ω resistors in the network shown in

Let the currents in the various meshes of the network are i1, i2, i3 and i4.
Applying KVL to various meshes of the network for mesh AHGBA
-3 (i1 – i4) – 20 (i1 – i2) = 0
-3 i1 +3 i4 – 20 i1 + 20 i2 = 0
-23 i1 + 20 i2 + 3 i4 = 0 ………..(1)
For mesh GFCBG
-3 (i2 – i4) – 20 (i2 – i3) – 20 (i2 – i1) = 0
-3 i2 + 3 i4 – 20 i2 + 20 i3 – 20 i2 + 20 i1 = 0
20 i1 - 43 i2 + 20 i3 + 3 i4 = 0 ………..(2)
For mesh FEDCF
-3 (i3 – i4) – 20 (i3) – 20 (i3 – i2) = 0
-3 i3 + 3 i4 – 20 i3 – 20 i3 + 20 i2 = 0
20 i2 - 43 i3 + 3 i4 = 0 ………..(3)
For mesh ABCDJIA.
-3 (i4 – i1) – 3 (i4 – i2 ) – 3 (i4 – i3) + 50 = 0
-3 i4 + 3 i1 – 3 i4 + 3 i2 – 3 i4 + 3 i3 + 50 = 0
3 i1 - 3 i2 + 3 i3 – 9 i4 = –50 ………..(4)
Subtracting equ (1) from equ (3)
20 i2 - 43 i3 + 3 i4 = 0 → (3)
-23 i1 + 20 i2 + 3 i4 = 0
____________________
23 i1 – 43 i3 =0 ………. (5)
23 i1 = 43 i3
i1 = 1.87 i3 ………….(6)
Substracting equ (2) from equ (3)
20 i2 - 43 i3 + 3 i4 = 0 → (3)
-20 i1 + 43 i2 – 20 i3 – 3 i4 = 0 → (2)
______________________
– 20 i1 + 63 i2 – 63 i3 = 0 ………. (7)
Sub equ (6) in equ (7)
-20 (1.87 i3) + 63 i2 – 63 i3 = 0
-37.4 i3 + 63 i2 – 63 i3 = 0
-100.4 i3 + 63 i2 = 0
63 i2 = 100.4 i3
i2 = 100.4/63 i3
i2 = 1.6 i3 ………..(8)
Substituting equ (6) & (8) in equ (1)
-23 i1 + 20 i2 + 3 i4 = 0
-23(1.87 i3) + 20(1.6 i3) + 3i4 = 0
-43.01 i3 + 32 i3 + 3 i4 = 0
-11.01 i3 + 3i4 = 0
3i4 = 11.01 i3
I4 = 11.01/3 i3
I4 = 3.67 i3 ………..(9)
Substituting the values of i1, i2 and i4 into equ (4)
3i1 + 3i2 + 3i3 – 9i4 = -50
3(1.87 i3) + 3(1.6 i3) + 3i3 − 9(3.67 i3) = -50
5.61 i3 + 4.8 i3 + 3 i3 - 33.03 i3 = -50
-19.62 i3 = -50
i3 = 2.55 A
i1 = 1.87 (2.55)
= 4.76 A
i2 = 1.6 (2.55)
= 4.08 A
i4 = 3.67 (2.55)
= 9.35 A
Voltage across branch AB
V1 = 3 × (i4 - i1)
= 3 × (9.35 - 4.76)
= 13.77 V
Voltage across branch BC
V2 = 3 × (i4 - i2)
= 3 × (9.35 - 4.08)
= 15.81 V
Voltage across branch CD
V3 = 3 × (i4 - i3)
= 3 × (9.35 - 2.55)
= 20.4 V
Example: 25
Find the current in the 8 Ω resistor in the circuit shown in figure.
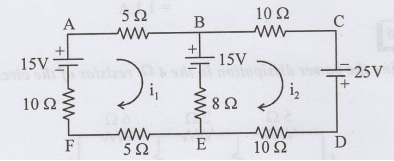
For mesh ABEFA
-10 (i1) + 15 – 5 i1 – 15 – 8 (i1 – i2) -5 i1 = 0
-10 i1 – 5 i1 – 8 i1 + 8 i2 – 5 i1 = 0
-28 i1 + 8 i2 = 0
-28 i1 = -8 i2
i2 = 28 i1/8 = 3.5 i1
For mesh BCDEB
-10 i2 + 25- 10 i2 – 8 (i2 – i1) + 15 = 0
-10 i2 + 25 – 10 i2 – 8 i2 + 8 i1 + 15 = 0
-28 i2 + 8 i1 + 40 = 0
40 = 28 i2 – 8 i1 ………..(2)
Sub i2 in equ (2)
40 = 28 (3.5 i1) - 8i1
40 = 98i1 - 8i1
40 = 90i1
i1 = 40/90 = 0.44 A
i2 = 3.5 (0.44)
= 1.54 A
current through 8 Ω resistor = i2 - i1
= 1.54 - 0.44
= 1.1 A
Example: 26
Determine the power dissipation in the 4 Ω resistor of the circuit shown in figure.

Assume three mesh currents i1, i2 and i3. The current flow through 4 Ω resistor is i2 - i3.
For mesh ABGHA
-5 i1 - 3 (i1 – i2) + 60 = 0
-5 i1- 3 i1 + 3 i2 + 60 = 0
60 = 8 i1 – 3 i2 …………(1)
For mesh BCFGB
-2 i2 - 4 (i2 – i3) – 3 (i2 – i1) = 0
-2 i2 – 4 i2 + 4 i3 – 3 i2 + 3 i1 = 0
– 3 i1 + 9 i2 – 4 i3 = 0 ………….(2)
For mesh CDEFC
-6 i3 - 20 - 4 (i3 – i2) = 0
-6 i3 - 20 – 4 i3 + 4 i2 = 0
-20 = - 4 i2 + 10 i1 …………(3)
Using the above three equations

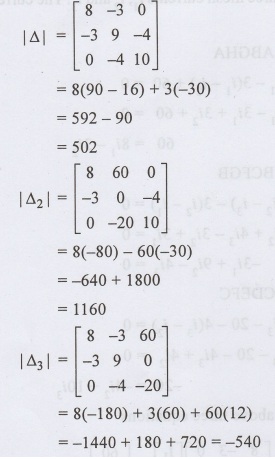
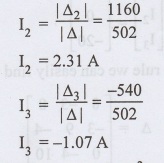
Power dissipated in 4Ω resistor = (i2 - i3)2 × 4
[2.31 - (-1.07)]2 × 4
= 45.69 W
Example: 27
For the circuit shown in fig. Find the current flowing through the 10 Ω resistor.
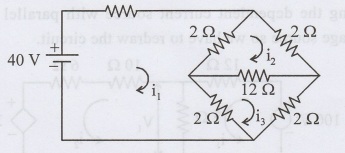
For loop: 1
-10 i1 - 2(i1 - i2) -2 (i1 - i3) + 40 = 0
-10 i1 – 2 i1 + 2 i2 – 2 i1 +2 i3 + 40 = 0
-14 i1 + 2 i2 +2 i3 + 40 = 0
40 = 14 i1 – 2 i2 – 2 i3 …………(1)
For loop: 2
-2 i2 - 12(i2 - i3) -2(i2 - i1) = 0
-2 i2 – 12 i2 + 12 i3 – 2 i2 + 2 i1 = 0
-16 i2 + 12 i3 + 2 i1 =
0 = −2i1 + 16i2 - 12i3 …………(2)
For loop : 3
-2 i3 - 12(i3 – i2) - 2(i3 - i1) = 0
-2 i3 – 12 i3 + 12 i2 – 2 i3 +2 i1 = 0
-16 i3+ 12 i2 + 2i1 = 0
0 = -2 i1 – 12 i2 + 16 i3 …………(3)
By solving the above three equations
i1 = 3.33 A, i2 = 1.67, A, i3 = 1.67 A
The current flowing through the 10Ω resistor is 3.33 A.
Example: 28
For the circuit shown in figure, find V1 using mesh analysis technique.

Converting the dependent current source with parallel resistance 6 Ω to dependent voltage source so we have to redraw the circuit.
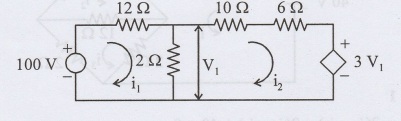
For mesh 1
−12 i1 − 2(i1 − i2) + 100 = 0
-12 i1 - 2 i1 + 2i2 + 100 = 0
100 = 14 i1 - 2i2 ………….(1)
For mesh 2
-10 i2 – 6 i2 - 3V1 - 2(i2 – i1) = 0
-16 i2 - 3V1 – 2 i2 + 2 i1 = 0
- 3V1 = – 2 i1 + 18 i2 ……………(2)
But
V1 = 2 (i1 - i2)
equ (2) becomes
-3(2(i1 - i2) = -2 i1 + 18 i2
-3(2i1 - 2i2) = -2i1 + 18 i2
-6i1 + 6i2 = -2i1 + 18 i2
0 = 4 i1 + 12 i2 …………..(3)
Solving equ (1) & (3)
i1 = 6.82 A, i2 = −2.27 A
V1 = 2(6.82 - (-2.27)
= 18.18 V
Basic Electrical and Electronics Engineering: Unit I: Electrical Circuits : Tag: : Electrical Circuits - Solved Example Problems [Mesh Analysis]
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

