Density of States (a) in Bulk Material (Three Dimension), Quantum Well (Two Dimensions)

DENSITY OF STATES

Density of states Z(E)dE is defined as the number of states per unit volume in an energy interval E and E + dE.

(or)

Density of states Z(E), is defined as the number of states per unit volume per unit energy around an energy dE.

where n = number of states per unit volume.

1. DENSITY OF STATES IN BULK MATERIAL (OR) DENSITY OF STATES IN THREE DIMENSION

Density of states Z(E), is defined as the number of states per unit volume per unit energy around an energy E.

Consider the case of an electron in a three-dimensional bounded region of space. we want to find how many quantum states lie within a particular energy range, say, between E and E + dE.

Explanation

Since we are dealing with almost a continum of energy levels, we may construct a space of points represented by the values ny, ny and n, and let each point with integer values of the coordinates represent an energy state as shown in Fig. 5.9.

Thus 'n' represents a vector to a point n_x, n_y, n_z (n² = n_x² + n_y² + n_z²) in three dimensional space.

Derivation

The number of available states with in a sphere of radius 'n' is given

by 

The factor 1/8 accounts for the fact that only one octant of the sphere is available.

The number of states within a sphere of radius (n + dn) is given by 

The number of available energy states lying in an energy interval E and E + dE

neglecting dn² and dn³

…....(1)

We know the energy levels for a particle in a box

…....(2)

m* is the effective mass of the particle at a given point in the heterostructure

……..(3)

……..(4)

…......(5)

Substitute Eqn. (3) and Eqn. (5) in Eqn. (1), we get

Put L³ = V = volume of the sphere.

……..(6)

According to Pauli's exclusion principle each energy level can occupy 2 electrons of opposite spin.

Multiply Eqn.(6) by 2, we get

Number of quantum states in the volume region

No. of quantum states per unit volume

No.of quantum states per unit volume per unit energy is given by 

Density of states………(7)

put h =  in Eqn.(7), we get

Density of states 

……….(8)

Eqn. (8) is called density of states in three dimension and

The Density of states in Bulk material is shown in Fig 5.10

2. DENSITY OF STATES IN QUANTUM WELL(OR) DENSITY OF STATES IN TWO DIMENSIONS

The quantum well can be displayed with dimensions of length L, where the electrons of effective mass are confined in the well as shown in Fig 5.11.

The two-dimensional density of states is the number of states per unit area and unit energy.

Explanation

Consider the electron in a two-dimensional bounded region of space. We want to find how many quantum states lie within a particular energy, say, between E and E + dE as shown in Fig. 5.12.

The reduced phase space now consists only the x-y plane and n_x and n_y coordinates.

In two-dimensional space, n² = n_x² + n_y².

Derivation

The number of available states within a circle of radius 'n' is given by

1/4 πn²

Hint: Area of the circle πn²

The factor 1/4 accounts for the fact that only are quater of the circle is available.

The number of states within a circle of radius n+dn is given by

The number of available energy states lying in an energy internal E and E+dE

As dn² is very small, we can neglect dn². we get

………..(10)

Substituting Eqn. (4) and Eqn. (5) in Eqn. (10) we get,

where

m* is the effective mass in the quantum well

Put L² = A = Area of the circle

……....(11)

According to Pauli's exclusion principle each energy level can occupy 2 electrons of opposite spin.

multiply Eqn. (11) by 2 we get

Number of quantum states per unit area and unit energy is

The Density of states in two-dimensional is given by

…….(12)

Where E₀ Ground state of quantum well system

….....(13)

Where E_n are the energies of quantized states and σ (E-E_n) the step function.

Inference

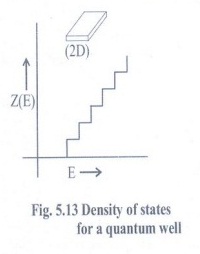
From Eqn. (12) we found that density of states in two-dimension is constant with respect to energy

i.e., Z(E)^2D ∞ E° = constant

For energies E≥E_o the 2-D density of states is a constant and does not depend on energy. If the 2-D semiconductor has more than one quantum state, each quantum state has a state density of equation (13). The total density can be written as

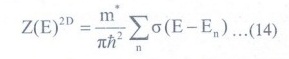……(14)

where E_n are the energies of quantized states and σ (E-E_n) is the step function.

The density of states in quantum well is shown in Fig. 5.13