Activation Functions

Activation Functions

• Activation functions also known as transfer function is used to map input nodes to output nodes in certain fashion.

• The activation function is the most important factor in a neural network which decided whether or not a neuron will be activated or not and transferred to the next layer.

• Activation functions help in normalizing the output between 0 to 1 or 1 to 1. It helps in the process of back propagation due to their differentiable property. During back propagation, loss function gets updated, and activation function helps the gradient descent curves to achieve their local minima.

• Activation function basically decides in any neural network that given input or receiving information is relevant or it is irrelevant.

• These activation function makes the multilayer network to have greater representational power than single layer network only when non-linearity is introduced.

• The input to the activation function is sum which is defined by the following equation.

Sum = I₁W₁ +I₂ W₂ +...+I_n W_n

= Σⁿ_j=1 I_j W_j + b

• Activation Function: Logistic Functions

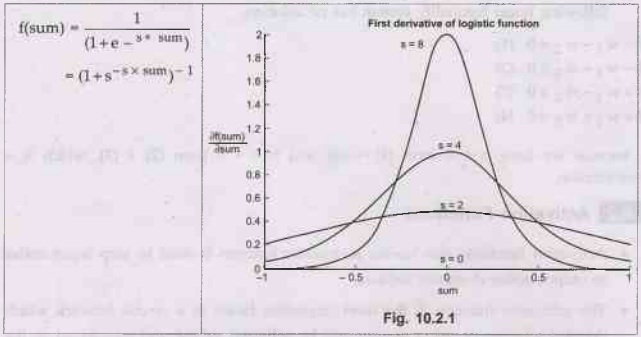
• Logistic function monotonically increases from a lower limit (0 or 1) to an upper limit (+1) as sum increases. In which values vary between 0 and 1, with a value of 0.5 when I is zero.

• Activation Function: Arc Tangent

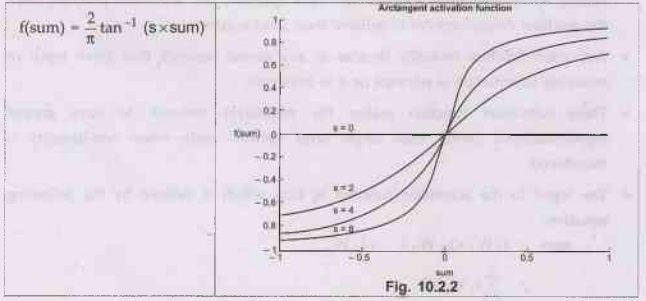
• Activation Function: Hyperbolic Tangent

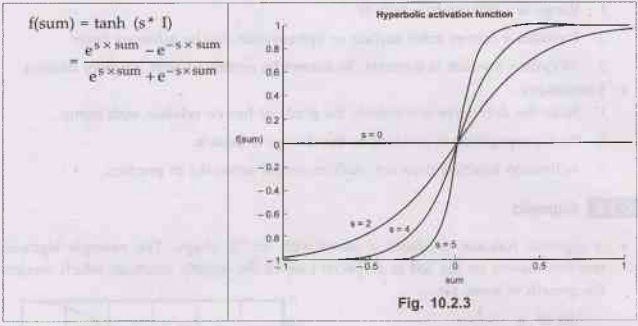
Identity or Linear Activation Function

• A linear activation is a mathematical equation used for obtaining output vectors with specific properties.

• It is a simple straight line activation function where our function is directly proportional to weighted sum of neurons or input.

• Linear activation functions are better in giving a wide range activations and a line of a positive slops may increase the firing rate as the input rate increases.

• Fig. 10.2.4 shows identity function.

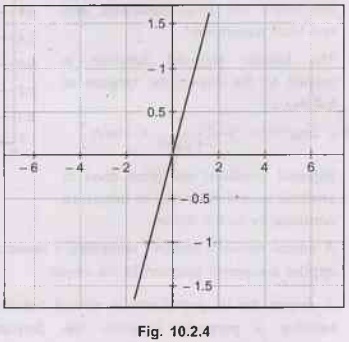
• The equation for linear activation function is :

f(x) = a.x

When a = 1 then f(x) = x and this is a special case known as identity.

• Properties:

1. Range is - infinity to + infinity

2. Provides a convex error surface so optimisation can be achieved faster.

3. df(x)/dx = a which is constant. So cannot be optimised with gradient descent.

• Limitations:

1. Since the derivative is constant, the gradient has no relation with input.

2. Back propagation is constant as the change is delta x.

3.Activation function does not work in neural networks in practice.

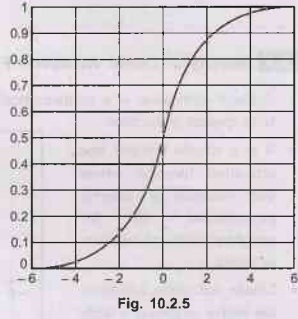
Sigmoid

• A sigmoid function produces a curve with an "S" shape. The example sigmoid function shown on the left is a special case of the logistic function, which models the growth of some set.

Sig (t) =1/1+e^-t

• In general, a sigmoid function is real-valued and differentiable, having a non-negative or non-positive first derivative, one local minimum, and one local maximum.

• The logistic sigmoid function is related to the hyperbolic tangent as follows:

1 - 2 sig (x) = 1- 2.1/1+e^–x = -tanh x/2

• Sigmoid functions are often used in artificial neural networks to introduce nonlinearity in the model.

• A neural network element computes a linear combination of its input signals, and applies a sigmoid function to the result.

• A reason for its popularity in neural networks is because the sigmoid function satisfies a property between the derivative and itself such that it is computationally easy to perform.

 d/dt sig (t) = sig(t) (1 - sig (t))