Two marks Questions with Answers

5.16 Two Marks Questions with Answers

Q.1What are B-trees ?

Ans. : B-tree is a multiway search tree of order m is an ordered tree where each node has at the most m children. If there are n number of children in a node then (n - 1) is the number of keys in the node.

Q.2 Enlist the properties of B-trees

Ans; The B-tree of order m should be constructed using following properties.

Rule 1: All the leaf nodes are on the botom level.

Rule 2: The root node should have at least two children.

Rule 3: All the internal nodes except root node have at least ceil (m/2) nonempty children. The ceil is a function such that ceil (3.4) = 4, ceil (9.3) = 10,

ceil (2.98) = 3 ceil (7) = 7.

Rule 4: Each leaf node must contain at least ceil (m/2) - 1 keys.

Q.3 What are the various operations that can be performed on B-trees ?

Ans. : Various operations that can be performed on B-Tress are

 1. Creation of B-Tree

2. Insertion of a node in B-Tree

3. Deletion of particular node from B-Tree

4. Searching a specific key value from B-Tree.

Q.4 What are the properties of binomial heaps.

1. The binomial heaps obey the min-heap or max-heap property.

2. For any non negative integer m, there is at the most one binomial tree in H whose root has degree m.

Q.5 Define a graph.

Ans. : A graph is a collection of two sets of V and E where V is finite non empty set of vertices and E is a finite non empty set of edges.

Vertices are nothing but the nodes in the graph and two adjacent vertices are joined by edges.

The graph is denoted by G = {V, E}.

Q.6 What are the storage representation of the graph? Or

 What are different ways to represent the graph.

Ans. : The graph can be represented by using arrays or linked list.

1. The adjacency matrix is a storage representation of the graph by which the graph is stored in two dimensional arrays.

2. The adjacency list is a storage representation of a graph by which the graph is stored in linked list.

Q.7 What are the applications of graph?

Ans. The graph theory is used widely in the computer science very widely. The applications of graph theory are -

1. In computer networking such as Local Area Network (LAN), Wide Area Networking (WAN) internetworking the graph is used.

2. In telephone cabling graph theory is effectively used.

3. In job scheduling algorithms the graph is used.

Q.8 Prove that the number of odd degree vertices in a connected graph should be even.

Ans; To prove this, consider connected graphs with odd degree vertices.

Q.9 What is an activity node graph?

Ans. : A graph in which vertices represent activities is called. an activity-node graph. In activity node graph the vertex is a weighted vertex.

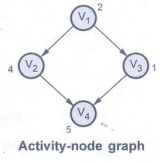
In this graph vertex V1 represents the beginning activity. The vertices V2 and a har V3 can be carried out in parallel. And finally activity at V4 can be performed.

Q.10 Define a graph. How it differs from tree?

Ans. : A graph is a collection of two sets of V and E where V is a finite non empty set of vertices and E is a finite non empty set of edges. Thus a graph is denoted by G = (V,E).

Thus graph and trees are both non-linear data structures but in trees there is special" node called root and in graph there is no root node.

Q.11 What is breadth first traversal?

Ans. : The breadth first traversal is a type of traversal in which the nodes on each level are displayed. For example

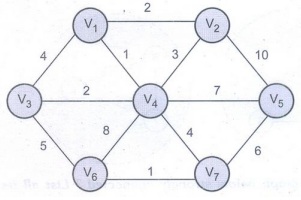
The BFS traversal is: V1 V2 V3 V4 V6 V7

Q.12 When a graph is said to be bipartite ?

Ans. : A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V. A bipartite graph is a graph that does not contain any odd-length cycles.

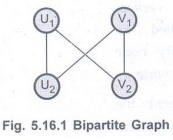
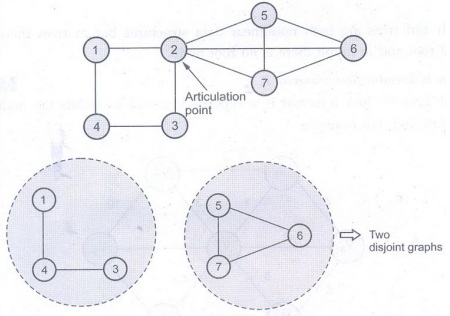
Q.13 What are articulation points ?

Ans. : Let G = (V,E) be a connected undirected graph, then an articulation point of graph G is a vertex whose removal disconnects graph G. This articulation point is a kind of cut-vertex.

For example

Q.14 Is the directed graph below strongly connected? List all its simple paths.

Ans. : Yes. Given graph is strongly connected, because all the nodes of a subgraph are reachable by all other nodes in the subgraph.

The simple paths are -

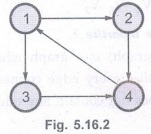
1) 1, 2, 4.

2) 1, 3, 4.

3) 2, 4, 1. 

4) 2, 4, 1, 3.

5) 3,4

6) 3, 4, 1.

7) 3, 4, 2.

8) 4, 1, 2.

9) 4, 1, 3.

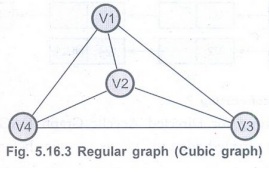
Q.15 Define regular graph.

Ans. : A regular graph is a kind of graph in which the degree of each vertex is the same. For example

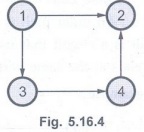
Q.16 What is weakly connected graph?

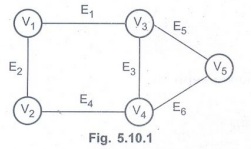
Ans. : A directed graph is called weakly connected graph when all the directed edges within a diagraph are replaced by undirected edges and produce an undirected graph in which there is a path from every node to every another node. For example –

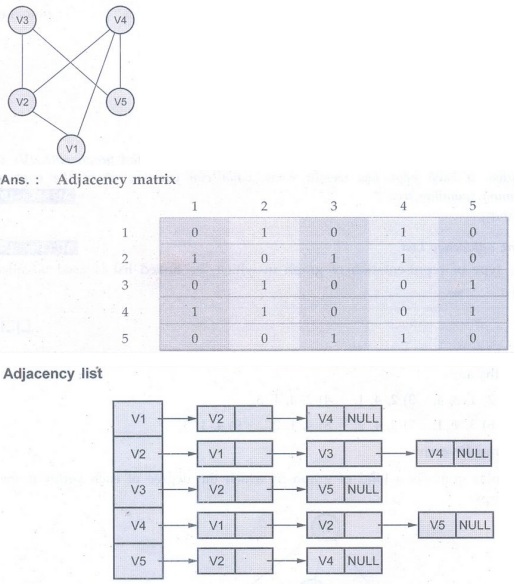
Q.17 Find the adjacency matrix and adjacency list for the following graph.

Q.18 What is topological sorting?

Ans; Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that every directed edge uv, vertex u comes before v in ordering.

Q.19 Define Euler circuits.

Ans. : An Euler path is a path that uses every edge of a graph exactly once. An Euler circuit is a circuit that uses every edge of a graph exactly once. An Euler circuit starts and ends at the same vertex.

For example:

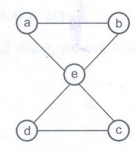
Q.20 What is Bi-connectivity ?

Ans. : 

Biconnected graphs are the graphs which can not be broken into two disconnected pieces (graphs) by connecting single edge. For example :

Q.21 Given a weighted undirected graph with IV nodes, Assume all weights are non negative. If each edge has weight <=w, what can you say about the cost of Minimum spanning tree ?

Ans. : O (V+E).

Q.22 Define adjacency List.

Ans; The type of representation of graph in which the linked list is used is called adjacency list.