Relational Algebra

Relational Algebra

AU: May-03,04,05,14,15,16,17,18, Dec.-02,06,07,08,11,15,16,17, Marks 16

There are two formal query languages associated with relational model and those are relational algebra and relational calculus.

• Definition: Relational algebra is a procedural query language which is used to access database tables to read data in different ways.

• The queries present in the relational algebra are denoted using operators.

• Every operator in relational algebra accepts relational instances (tables) as input and returns relational instance as output. For example-

• Each relational algebra is procedural. That means each relational query describes a step-by-step procedure for computing the desired answer, based on the order in which operators are applied in the query.

• A sequence of relational algebra operations forms a relational algebra expression, whose result will also be a relation that represents the result of a database query. The By composing the operators in relational expressions the complex relation can be defined.

Relational Operations

Various types of relational operations are as follows-

(1) Selection:

• This operation is used to fetch the rows or tuples from the table(relation).

• Syntax: The syntax is

σ_predicate(relation)

Where σrepresents the select operation. The predicate denotes some logic using which the data from the relation (table) is selected.

• For example - Consider the relation student as follows-

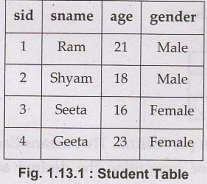
Query: Fetch students with age more than 18

We can write it in relational algebra as

Σ_age>>18 (student)

The output will be-

We can also specify conditions using and, or operators.

(2)Projection :

• Project operation is used to project only a certain set of attributes of a relation. That means if you want to see only the names all of the students in the Student table, then you can use Project operation.

• Thus to display particular column from the relation, the projection operator is used.

• It will only project or show the columns or attributes asked for, and will also vait remove duplicate data from the columns.

• Syntax:

ПС1, С2... (r)                                                                                                      

where C1, C2 etc. are attribute names(column names).

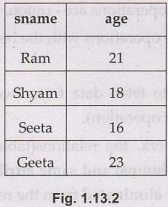
• For example - Consider the Student table given in Fig. 1.13.2.

Query: Display the name and age all the students

This can be written in relational algebra as

П_{sname, age} (Student)

Above statement will show us only the Name and Age columns for all the rows of data in Student table.

(3) Cartesian product:

• This is used to combine data from two different relations(tables) into one and fetch data from the combined relation.

• Syntax: A x B

• For example: Suppose there are two tables named Student and Reserve as follows

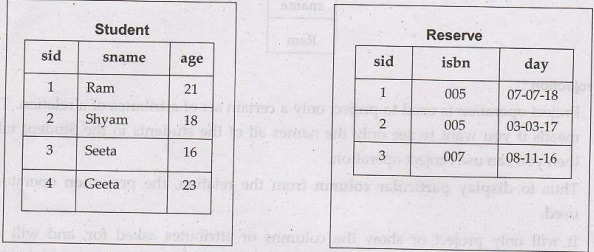
Query: Find the names of all the students who have reserved isbn = 005. To satisfy this query we need to extract data from two table. Hence the cartesian product operator is used as

(σ_{Student.sid = Reserve.sid ˄ Reserve.Isbn = 005} (Student × Reserve)

As an output we will get

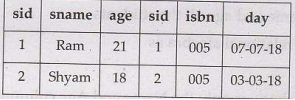
Note:that although the Sid columns is same, it is repeated.

(4) Set operations: Various set operations are - union, intersection and set-difference. Let us understand each of these operations with the help of examples.

(i) Union:

• This operation is used to fetch data from two relations(tables) or temporary relation(result of another operation).

• For this operation to work, the relations(tables) specified should have same number of attributes(columns) and same attribute domain. Also the duplicate tuples are automatically eliminated from the result.

• Syntax: AUB

• Where A and B are relations.

• For example: If there are two tables student and books as follows-

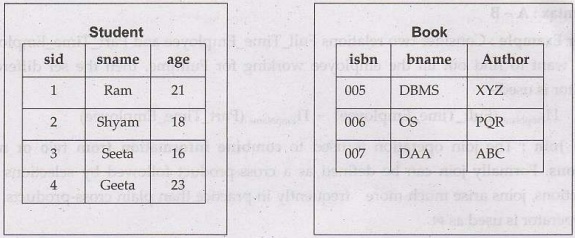
• Query: We want to display both the student name and book names from both the tables then

П_sname (Student) U П_bname (Book)

(ii) Intersection:

• This operation is used to fetch data from both tables which is common in both the tables.

• Syntax: A ∩ B

where A and B are relations.

• Example - Consider two tables - Student and Worker

• Query: If we want to find out the names of the students who are working in a company then 300

П_name (Student) ∩ П_name (Worker)

(iii) Set-Difference: The result of set difference operation is tuples, which are present in one relation but are not in the second relation.

Syntax: A - B

For Example: Consider two relations Full_Time_Employee and Part_Time_Employee, if we want to find out all the employee working for Fulltime, then the set difference operator is used -

П_EmpName(Full Time_Employee) – П_EmpName(Part_Time_Employee)

(5) Join:The join operation is used to combine information from two or more relations. Formally join can be defined as a cross-product followed by selections and projections, joins arise much more frequently in practice than plain cross-products. The join operator is used as

A) Inner Join

There are three types of joins used in relational algebra

i) Conditional join: This is an operation in which information from two tables is combined using some condition and this condition is specified along with the join operator.

A_c B = σ_c (A x B)

Thus  is defined to be a cross-product followed by a selection. Note that the condition c can refer to attributes of both A and B. The condition C can be specified using <,<,>,< or = operators.

For example consider two table student and reserve as follows-

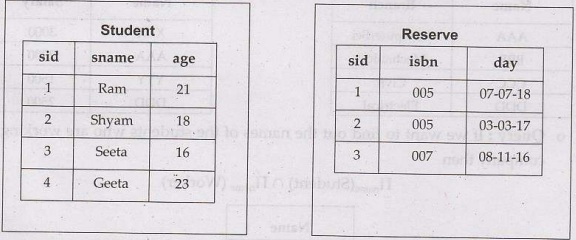
If we want the names of students with sid(Student) = sid (Reserve) and isbn = 005,then we can write it using Cartesian product as -

(σ((Student.sid = Reserve.sid) ∩(Reserve.(isbn) =005)) (Student × Reserve))

Here there are two conditions as

i) (Student.sid =Reserve.sid) and ii) (Reserve.isbn = 005) which are joined by∩operator.

Now we can use _c instead of above statement and write it as -

(Student _{( Student.sid - Reserve.sid) ˄ (Reserve.(Isbn) - 005)} Reserve))

The result will be-

ii) Equijoin: This is a kind of join in which there is equality condition between two attributes(columns) of relations(tables). For example - If there are two table Book and Reserve table and we want to find the book which is reserved by the student having isbn 005 and name of the book is 'DBMS', then :

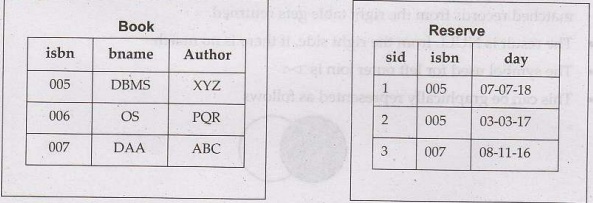
(Obname='DBMS' (Book (Book.isbn = Reserve.isbn) Reserve)

Then we get

iii) Natural Join: When there are common columns and we have to equate these common columns then we use natural join. The symbol for natural join is simply  without any condition. For example, consider two tables-

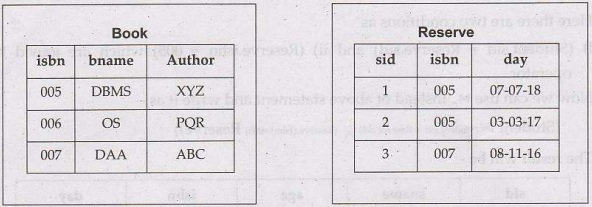
Now if we want to list the books that are reserved, then that means we want to match Books.isbn with Reserve.isbn. Hence it will be simply Books Reserve

B) Outer Join

There are three types of outer joins - Left outer join, Right outer join and Full outer join.

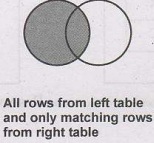
(1) Left Outer join

• This is a type of join in which all the records from left table are returned and the matched records from the right table gets returned.

• The result is NULL from the right side, if there is no match.

• The symbol used for left outer join is 

• This can be graphically represented as follows

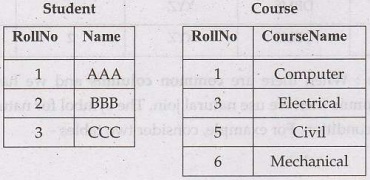
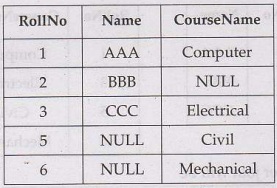
• For example - Consider two tables Student and Course as follows –

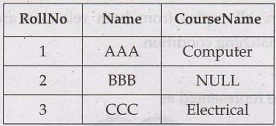
The result of Left outer join will be

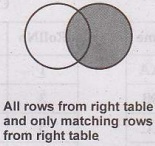
(2) Right Outer join

• This is a type of join in which all the records from right table are returned and the matched records from the left table gets returned.

• The result is NULL from the left side, if there is no match.

• The symbol used for right outer join is 

• This can be graphically represented as follows

• For example - Consider two tables Student and Course as follows-

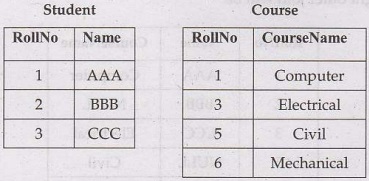
The result of Right outer join will be

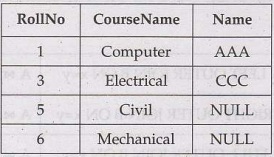
(3) Full Outer join

• In a full outer join, all tuples from both relations are included in the result, irrespective of the matching condition.

• It is denoted by

• Graphically it can be represented as

• For example - Consider two tables Student and Course as follows –

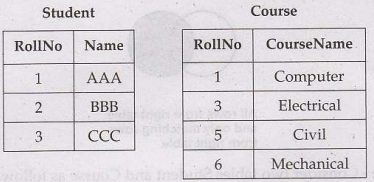
The result of Right outer join will be

The symbols used are –

(6) Rename operation: This operation is used to rename the output relation for any query operation which returns result like Select, Project etc. Or to simply rename a relation(table). The operator ρ(rho) is used for renaming.

Syntax: ρ (RelationNew, RelationOld)

For example: If you want to create a relation Student_names with sid and sname from Student, it can be done using rename operator as:

ρ(Student_names, (Π_sid.sname (Student))

(7) Divide operation:The division operator is used when we have to evaluate queries which contain the keyword ALL.

It is denoted by A/B where A and B are instances of relation.

Formal Definition of Division Operation: The operation A/B is define as the set of all x values (in the form of unary tuples) such that for every y value in (a tuple of) B, there is a tuple <x,y> in A.

For example - Find all the customers having accounts in all the branches. For that consider two tables - Customer and Account as

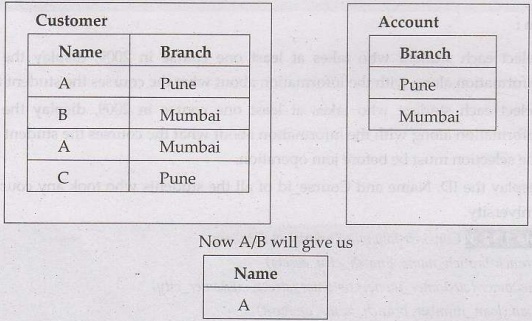
Here We check all the branches from Account table against all the names from Customer table. We can then find that only customer A has all the accounts in all the branches.

Review Questions

1. Explain select, project, cartesian product and join operations in relational algebra with an example lebeidi enne roberts AU: May-18, Marks 13, Dec.-16, Marks 6

2. List operations of relational algebra and purpose of each with example. AU: May-17, Marks 5

3.Differentiate between foreign key constraints and referential integrity constraints with suitable example. AU: Dec.-17, Marks 6

4. Explain various operations in relational algebra with examples

AU: May-03, Marks 10, Dec-07, Marks 8, Dec.- 08, Marks 10, May-14, Marks 16

5. Explain all join operations in relational algebra. AU: May-05, Marks 8

6. Briefly explain relational algebra.

AU: May-04, Marks 8

7. What is rename operation in relational algebra ? Illustrate your answer with example.

AU: Dec.-02, Marks 2