Minimum Spanning Tree

Minimum Spanning Tree

Spanning tree

A spanning tree of a graph G is a subgraph which is basically a tree and it contains all the vertices of G containing no circuit.

Minimum spanning tree

A minimum spanning tree of a weighted connected graph G is a spanning tree with minimum or smallest weight.

Weight of the tree

A weight of the tree is defined as the sum of weights of all its edges.

For example:

Consider a graph G as given below. This graph is called weighted connected graph because some weights are given along every edge and the graph is a connected graph.

Applications of spanning trees :

1. Spanning trees are very important in designing efficient routing algorithms.

2. Spanning trees have wide applications in many areas such as network design.

Prim's Algorithm

Let us understand the prim's algorithm with the help of example.

Example:

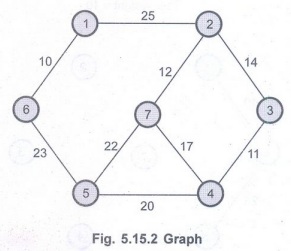
Consider the graph given below :

Now, we will consider all the vertices first. Then we will select an edge with minimum weight. The algorithm proceeds by selecting adjacent edges with minimum weight. Care should be taken for not forming circuit.

C program m

/****************************************************************

This program is to implement Prim's Algorithm using Greedy Method ****************************************************************/

#include<stdio.h>

#include<conio.h>

#define SIZE 20

#define INFINITY 32767

/*This function finds the minimal spanning tree by Prim's Algorithm */

void Prim(int G[][SIZE], int nodes)

{

int tree[SIZE], i, j, k;

int min_dist, v1, v2,total=0;

// Initialize the selected vertices list

for (i=0; i<nodes; i++)

tree[i] = 0;

printf("\n\n The Minimal Spanning Tree Is :\n");

tree[0] = 1;

for (k=1; k<=nodes-1; k++)

{

min_dist = INFINITY;

//initially assign minimum dist as infinity

for (i=0; i<=nodes-1; i++)

{

for (j=0; j<=nodes-1; j++)

{

if (G[i][j] && ((tree[i] && !tree[j]) || (!tree[i] && tree[j])))

{

if (G[i][j] <min_dist)

{

min_dist=G[i][j];

v1 = i;

v2 = j;

}

}

}

}

printf("\n Edge (%d %d ) and weight = %d",v1,v2,min_dist);

tree[v1] = tree [v2] = 1;

total = total+min_dist;

}

printf("\n\n\t Total Path Length Is = %d",total);

}

void main()

{

int G[SIZE][SIZE], nodes;

int v1, v2, length, i, j, n;

clrscr();

printf("\n\t Prim'S Algorithm\n");

printf("\n Enter Number of Nodes in The Graph ");

scanf("%d",&nodes);

printf("\n Enter Number of Edges in The Graph ");

 scanf("%d",&n);

for (i=0; i<nodes; i++) // Initialize the graph

for (j=0; j<nodes; j++)

G[i][j] = 0;

//entering weighted graph

printf("\n Enter edges and weights \n");

for (i=0; i<n; i++)

{

printf("\n Enter Edge by V1 and V2 :");

printf("[Read the graph from starting node 0]");

 scanf("%d %d", &v1,&v2);

printf("\n Enter corresponding weight :");

scanf("%d", &length);

G[v1][v2] = G[v2][v1] = length;

}

getch();

printf("\n\t");

clrscr();

Prim(G,nodes);

getch();

}

Output

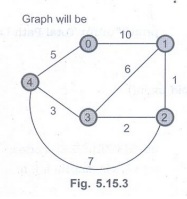
Prim'S Algorithm

Enter Number of Nodes in The Graph 5

Enter Number of Edges in The Graph 7

Enter edges and weights

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 0 1

Enter corresponding weight :10

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 1 2

Enter corresponding weight :1

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 2 3

Enter corresponding weight :2

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 3 4

Enter corresponding weight :3

Enter Edge by V1 and V2 [Read the graph from starting node 0] 4 0

Enter corresponding weight :5

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 1 3

Enter corresponding weight :6

Enter Edge by V1 and V2 : [Read the graph from starting node 0] 4 2

Enter corresponding weight :7

The Minimal Spanning Tree Is :

Edge(0 4) and weight = 5

Edge(3 4) and weight = 3

Edge(2 3) and weight = 2

Edge(1 2) and weight = 1

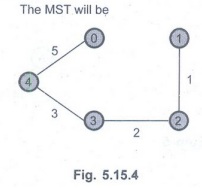
Total Path Length Is = 11

Ex. 5.15.1 Consider the following weighted graph.

Give the list of edges in the MST in the order that Prim's algorithm inserts them. Start Prim's algorithm from vertex A.

Ex. 5.15.2 Discuss about the algorithm and Pseudo-code to find the Minimum Spanning Tree using Prim's Algorithm. Find the Minimum Spanning tree for the graph shown below.

Ex. 5.15.3 Give the Pseudo code for Prim's algorithm and apply the same to find the minimum spanning tree of the graph shown below:

Kruskal's Algorithm

Kruskal's algorithm is another algorithm of obtaining minimum spanning tree. This algorithm is discovered by a second year graduate student Joseph Kruskal. In this algorithm always the minimum cost edge has to be selected. But it is not necessary that selected optimum edge is adjacent.

Let us understand this algorithm with the help of some example.

Example :

Consider the graph given below:

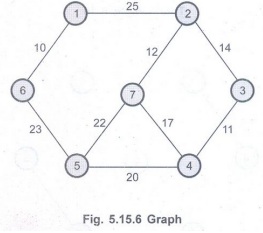
First we will select all the vertices. Then an edge with optimum weight is selected from heap, even though it is not adjacent to previously selected edge. Care should be taken for not forming circuit.

Ex. 5.15.4 Apply Kruskal's algorithm to find a minimum spanning tree of the following graph.

C program

/*****************************************************************

Implementation of Kruskal's Algorithm

*****************************************************************/

#include<stdio.h>

#define INFINITY 999

typedef struct Graph

{

int v1;

int v2;

int cost;

}GR;

GR G[20];

int tot_edges,tot_nodes;

void create();

void spanning_tree();

int Minimum(int);

void main()

{

printf("\n\t Graph Creation by adjacency matrix ");

create();

spanning_tree();

}

void create()

{

int k;

printf("\n Enter Total number of nodes: ");

scanf("%d", &tot_nodes);

printf("\n Enter Total number of edges: ");

scanf("%d", &tot_edges);

for(k=0;k<tot_edges;k++)

{

printf("\n Enter Edge in (V1 V2)form ");

scanf("%d%d",&G[k].v1,&G[k].v2);

printf("\n Enter Corresponding Cost ");

 scanf("%d", &G[k].cost);

}

}

void spanning_tree()

{

int count,k,v1, v2,i,j,tree [10][10],pos,parent[10];

int sum;

int Find(int v2,int parent[]);

void Union(int i,int j,int parent[]);

count=0;

k=0;

sum=0;

for(i=0;i<tot_nodes;i++)

parent[i]=i;

while(count!=tot_nodes-1)

{

pos=Minimum(tot_edges);//finding the minimum cost edge

 if(pos==-1)//Perhaps no node in the graph

break;

v1=G[pos].v1;

v2=G[pos].v2;

i=Find(v1,parent);

j=Find(v2,parent);

if(i!=j)

{

tree[k][0]=v1;//storing the minimum edge in array tree[]

tree[k][1]=v2;

k++;

count++;

sum+=G[pos].cost;//accumulating the total cost of MST

Union(i,j,parent);

}

G[pos].cost=INFINITY;

}

if(count==tot_nodes-1)

{

printf("\n Spanning tree is...");

printf("\n-----------------\n");

for(i=0;i<tot_nodes-1;i++)

{

printf("[%d", tree[i][0]);

printf("-");

printf("%d",tree[i][1]);

printf("1");

}

printf("\n----------------");

printf("\nCost of Spanning Tree is=%d",sum);

}

else

{

printf("There is no Spanning Tree");

}

}

int Minimum(int n)

{

int i,small,pos;

small=INFINITY;

pos=-1;

for(i=0;i<n;i++)

{

if(G[i].cost<small)

{

small=G[i].cost;

pos=i;

}

}

return pos;

}

int Find(int v2,int parent[])

{

while(parent[v2]!=v2)

{

v2=parent[v2];

}

return v2;

}

void Union(int i,int j,int parent[])

{

if(i<j)

parent[j]=i;

else

parent[i]=j;

}

Output

Graph Creation by adjacency matrix

Enter Total number of nodes: 4

Enter Total number of edges: 5

Enter Edge in (V1 V2)form 1 2

Enter Corresponding Cost 2

Enter Edge in (V1 V2)form 1 4

Enter Corresponding Cost 1

Enter Edge in (V1 V2)form 1 3

 Enter Corresponding Cost 3

Enter Edge in (V1 V2)form 2 3

Enter Corresponding Cost 3

Enter Edge in (V1 V2)form 43

Enter Corresponding Cost 5

Spanning tree is...

-----------------------

[1-4][1-2][1-3]

-----------------------

Cost of Spanning Tree is = 6

Difference between Prim's And Kruskal's Algorithm