Example on Normalization

Examples on Normalization   

 AU: Dec.-19, Marks 9

Example 2.15.1 Study the relation given below and state what level of normalization can be achieved and normalize it upto that level.

Solution:

Reason for the given relation being unnormalized

1. Observe order for many items.

2. Item lines has many attributes-called composite attributes.

3. Each tuple has variable length.

4. Difficult to store due to non-uniformity.

5. Given item code difficult to find qty-ordered and hence called Unnormalized relation.

For conversion to First Normal Form -

• Identify the composite attributes, convert the composite attributes to individual attributes.

• Duplicate the common attributes as many times as lines in composite attribute.

• Every attribute now describes single property and not multiple properties, some data will be duplicated.

• Now this is called First normal form (1NF) also called flat file.

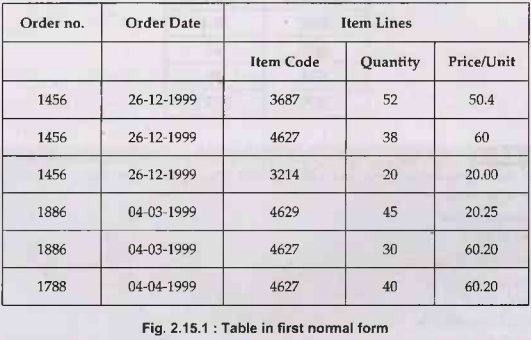
• The above table has insertion, deletion and update anomalies. For instance - if we delete order no. 1886, then the item code 4629 gets lost. Similarly if we update 4627, then all instances of 4627 need to be changed.

• We need to convert 2NF if it is in 1NF. The non-key attributes are functionally dependent on key attribute and if there is a composite key then no non-key attribute is functionally depend on one part of the key.

• The table can be converted to 2NF as follows -

Orders

Order Details

Prices

Example 2.15.2 A software contract and consultancy firm maintains details of all the various projects in which its employees are currently involved. These details comprise:

• Employee Number

• Employee Name

• Date of Birth

• Department Code

• Department Name Project Code

• Project Description

• Project Supervisor

Assume the following:

• Each employee number is unique.

• Each department has a single department code.

• Each project has a single code and supervisor.

• Each employee may work on one or more projects.

• Employee names need not necessarily be unique.

• Project Code, Project Description and Project Supervisor are repeating fields.

Normalise this data to Third Normal Form.

Solution:

Un-Normalized Form

Employee Number, Employee Name,Date of Birth, Department Code, Department Name, Project Code, Project Description, Project Supervisor

1NF

Employee Number, Employee Name___Date of Birth

Department Code, Department Name

Employee Number. Project Code. Project Description,_Project Supervisor

2NF

Employee Number, Employee Name,_Date of Birth,_Department Code,__Department Name Employee Number, Project Code,

Project Code, Project Description, Project Supervisor     

3NF

Employee Number, Employee Name___Date of Birth,*Department Code

Department Code, Department Name

Employee Number, Project Code

Project Code, Project Description, Project Supervisor

Example 2.15.3 What is normalization?Normalize below given relation upto 3NF STUDENT.

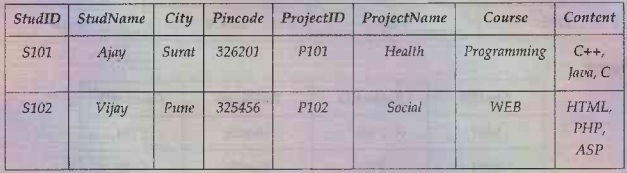
Solution: For converting the given schema to first normal form, we will arrange it in such a way that have each tuple contains single record. For that purpose we need to split the schema into two tables namely Student and Projects

1NF

Student

Projects

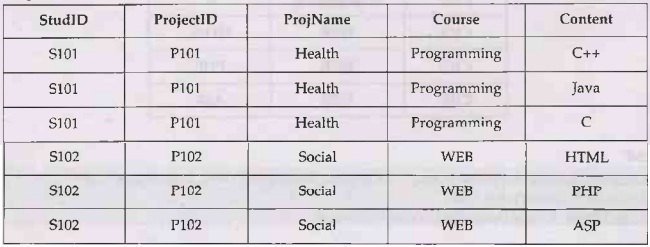
2NF

For a table to be in 2NF, there should not be any partial dependency.

Student

Project

CourseDetails

3NF: There was a transitive dependency in 2NF tables because city is associated with student ID and city depends upon zip code. Hence the transitive dependency is removed to covert table into 3NF. The required 3NF schema is as below -

Student

Student_Address

Project

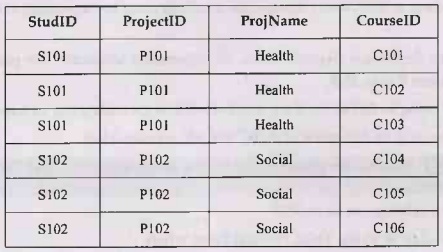
CourseDetails

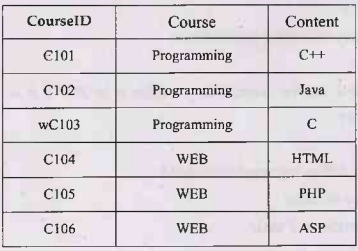
Example 2.15.4 Consider table R(A,B,C,D,E) with FDs as A->B, BC->E, and ED->A.The table is in which normal form? Justify your answer.

Solution:

Step 1: We will first find out the candidate keys for given relation R

(ACD)⁺ = {A,B,C,D,E}

(BCD)⁺ = {A,B,C,D,E}

(CDE)⁺ = {A,B,C,D,E}

Step 2: Let A->B, the ACD is candidate key and A is a partial key, B is a prime attribute(i.e. it is also part of candidate key). Hence A->B is not a partial functional dependency.

Similarly in BC->E and ED->A,

E and A are prime-attributes and hence both are not partial functional dependencies. Hence R is in 2NF.

Step 3: According to 3NF, every non-prime attribute must be dependent on the candidate key.

In the given functional dependencies, all dependent attributes are prime-attributes. Hence the relation R is in 3NF.

Step 4: For R being in BCNF for X->Y the X should be candidate key or super key.

The table is not in BCNF, none of A, BC and ED contain a key.

Example 2.15.5 Prove the statement "Every relation which is in BCNF is in 3NF but the converse is not true".

Solution: For a relations to be in 3NF

A table is said to be in the Third Normal Form when,

i) It is in the Second Normal form. (i.e. it does not have partial functional dependency)

ii) It doesn't have transitive dependency.

Or in other words

In other words 3NF can be defined as: A table is in 3NF if it is in 2NF and for each

functional dependency

X-> Y

At least one of the following conditions hold:

iii) X is a super key of table

iv) Y is a prime attribute of table

For a relation to be in BCNF

(1) It should be in 3NF

(2) A 3NF table which does not have multiple overlapping candidate keys is said to be in BCNF.

For proving that the table can be in 3NF but not in BCNF consider following relation R(Student, Subject, Teacher) . Consider following are FDs

(Subject, Student)-> Teacher

Because subject and student combination gives unique teacher. A

Teacher ->Subject

Because each teacher teaches only Subject.D.

(Teacher, Student)->Subject

• So, this relation is in 3NF as every non-key attribute is non-transitively fully sim noinu grian won Buil functional dependent on the primary key.

• But it is not in BCNF. Because this is a case of overlapping of candidate keys because there are two composite candidate keys:

      • (Subject, Student)

      • (Teacher, Student)

And Student is a common attribute in both the candidate keys.

So we need to normalize the above table to BCNF. For that purpose we must set Teacher to be a candidate keylot as TME of

The decomposition of above takes place as follows

R1(Student, Teacher)

R2(Teacher, Subject)

Now table is in 3NF, as well as in BCNF.

This show that the relation Every relation which is in BCNF is in 3NF but the converse is not true.

Example 2.15.6 Consider the relation R = {A, B, C, D, E, F, G, H, I, J) and the set of functional dependencies F = {{A, B} - C, A (D, E), B →F, F{G, H), D→{I, J} }

1. What is the key for R? Demonstrate it using the inference rules.

2. Decompose R into 2NF, then 3NF relations.

Solution: Let,

A → DE (given)

A → D, A→E (decomposition rule)

As          D → IJ, A → IJ

Using union rule we get

A → DEIJ

As         A→A

we get  A→ ADEIJ

Using augmentation rule we compute AB

AB → ABDEIJ

But

AB→C (given)

AB → ABCDEIJ

B→ F (given)        F→GH       B→GH (transitivity)

AB→AGH is also true

Similarly       AB→AF           B → F (given)

Thus now using union rule

AB → ABCDEFGHIJ

AB is a key

The table can be converted to 2NF as

R1=(A, B, C)

R2=(A, D, E, I, J)

R3= (B, F, G, H)

The above 2NF relations can be converted to 3NF as follows:

R1=(A, B, C)

R2 = (A, D, E)

R3=(D, I, J)

R4 = (B, E)

R5= (E, G, H).

Example 2.15.7 Consider a relation R(ABC) with following FD A->B, B->C and C->A. What is the normal form of R?

Solution:

Step 1: We will find the candidate key

(A)⁺={ABC} = R

(B)⁺= {ABC) = R

(C)⁺={ABC) = R

Hence A, B and C all are candidate keys

Prime attributes = {A,B,C}

Non prime attribute {}

Step 2: For R being in BCNF for X->Y the X should be candidate key or super key. From above FDs

  • Consider A->B in which A is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider B->C in which B is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider C->A in which C is a candidate key or super key. Condition for BCNF is satisfied.

This shows that the given relation R is in BCNF.

Example 2.15.8 Consider the Table 2.15.1 and answer to queries given below.

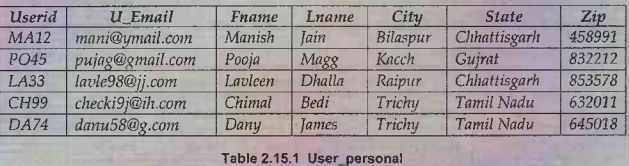
1) In this table in first normal form - 1NF? Justify and normalize to 1 NF if needed.

2) Is this table in second normal form - 2NF ? Justify and normalize to 2NF if needed.

3) Is User_personal in third normal form - 3NF? Justify and normalize to 3NF if needed.

Solution:

1) All the rows contain only one atomic value.

Hence table is in 1NF.

2) For identifying if table is in 2NF, we must check two rules -

Rule 1: The table must be in 1NF.

Rule 2: There should not be any partial key dependency.

As we know, that table is in 1NF, Rule 1 is said to be satisfied.

For checking Rule 2, first find out the primary keys.

Assume that, User_id and zip are to primary keys.

F = {User_id → U_Email Fname Lname City State Zip

Zip→ City State

}

Note that Userid can uniquely identify all the attributes of given relation. There is no partial dependency for identifying all the attributes. Hence rule 2 is said to be fulfilled. Therefore table is in 2NF.

3) To verify 3NF, the conditions are -

Rule 1: Table should be in 2NF

Rule 2: There should not be transitive dependency in the table. The table is already in 2NF, hence rule 1 is already satisfied.

Given table shows transitive dependency. It is as follows:

Userid → Zip and Zip→ City State

To bring the relation in 3NF, we have to decompose table into two tables

User_personal (Userid, U_Email, Fname, Lname, Zip)

Address (Zip, City, State)

The underlined fields are primary keys of respective tables. The tables are as follows:

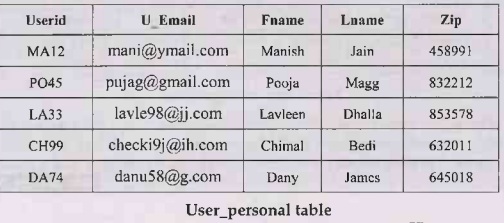
Example 2.15.9 What is the difference between 3NF and BCNF?

Solution: