Decomposition

Decomposition

• Decomposition is the process of breaking down one table into multiple tables.

• Formal definition of decomposition is -

• A decomposition of relation Schema R consists of replacing the relation Schema by two relation schema that each contain a subset of attributes of R and together include all attributes of R by storing projections of the instance.

• For example - Consider the following table

Employee_Department table as follows -

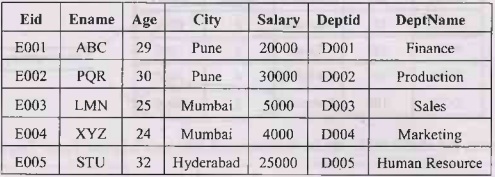
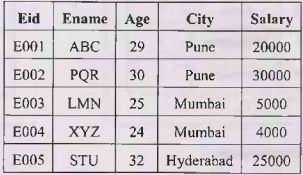
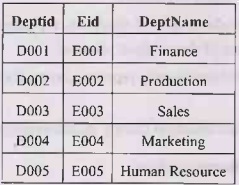
We can decompose the above relation Schema into two relation schemas as Employee (Eid, Ename, Age, City, Salary) and Department (Deptid, Eid, DeptName) as follows –

Employee Table

Department Table

• The decomposition is used for eliminating redundancy.

• For example: Consider following relation Schema R in which we assume that the grade determines the salary, the redundancy is caused

Schema R

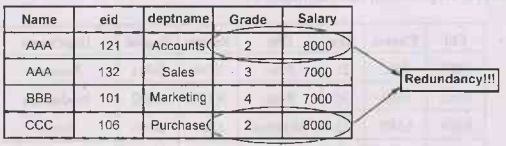
• Hence, the above table can be decomposed into two Schema S and T as follows:

Problems Related to Decomposition:

Following are the potential problems to consider:

1) Some queries become more expensive.

2) Given instances of the decomposed relations, we may not be able to reconstruct the corresponding instance of the original relation!

3) Checking some dependencies may require joining the instances of the decomposed relations.

4) There may be loss of information during decomposition.

Properties Associated With Decomposition

There are two properties associated with decomposition and those are -

1) Loss-less Join or non Loss Decomposition: When all information found in the original database is preserved after decomposition, we call it as loss less or non loss decomposition.

2) Dependency Preservation:This is a property in which the constraints on the original table can be maintained by simply enforcing some constraints on each of the smaller relations.

Non-loss Decomposition or Loss-less Join

The lossless join can be defined using following three conditions:

i) Union of attributes of R1 and R2 must be equal to attribute of R. Each attribute of R must be either in R1 or in R2.

Att(R1) U Att(R2) = Att(R)

ii) Intersection of attributes of R1 and R2 must not be NULL.

Att(R1) Att(R2) ≠ Φ

iii)Common attribute must be a key for at least one relation (R1 or R2)

Att(R1) Att(R2) -> Att(R1)

Att (R1) Att (R2) -> Att (R2)

Example 2.10.1 Consider the following relation R(A,B,C,D)and FDs A->BC, is the decomposition of R into R1(A,B,C), R2(A,D). Check if the decomposition is lossless join or not.

Solution:

Step 1: Here Att(R1) U Att(R2) = Att(R) i.e R1(A,B,C) u R2(A,D)=(A,B,C,D) i.e R.

Step 2: Here R1 R2={A}. Thus Att(R1) Att(R2)≠Φ. Here the second condition gets satisfied.

Step 3: Att(R1) n Att(R2) -> {A}. Now (A)*={A,B,C) ϵ attributes of R1. Thus the third condition gets satisfied.

This shows that the given decomposition is a lossless join.

Example 2.10.2 Consider the following relation R(A,B,C,D,E,F) and FDs A->BC, C->A, D- >E, F->A, E->D is the decomposition of R into R1(A,C,D), R2(B,C,D), and R3(E,F,D). Check for lossless.

Solution:

Step 1: R1UR2UR3 = R. Here the first condition for checking lossless join is satisfied as (A,C,D)U (B,C,D) U (E,F,D) = {A,B,C,D,E,F) which is nothing but R.

Step 2: Consider R1 ∩ R2 = {CD) and R2 R3 = {D}. Hence second condition of intersection not being gets satisfied.

Step 3: Now, consider R1(A,C,D) and R2(B,C,D). We find R1/R2 = {CD}

(CD)* = {ABCDE} = attributes of R1 i.e.{A,C,D). Hence condition 3 for checking lossless join for R1 and R2 gets satisfied.

Step 4: Now, consider R2(B,C,D) and R3(E,F,D). We find R2 R3 = {D}. (D)*={D,E} which is neither complete set of attributes of R2 or R3.[Note that F is missing for being attribute of R3].

Hence it is not lossless join decomposition. Or in other words we can say it is a lossy decomposition.

Example 2.10.3 Suppose that we decompose schema R=(A,B,C,D,E) into (A,B,C) (C,D,E) Show that it is not a lossless decomposition.

Solution:

Step 1: Here we need to assume some data for the attributes A, B, C, D, and E. Using this data we can represent the relation as follows -

Relation R

Relation R1 = (A,B,C)

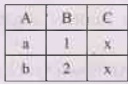
Relation R2 = (C,D,E)

Step 2: Now we will join these tables using natural join, i.e. the join based on common attribute C. We get R1 R2 as

Clearly R1  R2 R. Hence it is not lossless decomposition.

Dependency Preservation

• Definition: A Decomposition D = {R1, R2, R3....Rn} of R is dependency preserving for a set F of Functional dependency if - (F1 U F2 U... U Fm) = F.

• If decomposition is not dependency-preserving, some dependency is lost in the decomposition.

Example 2.10.4 Consider the relation R (A, B, C) for functional dependency set (A-> B and B-> C) which is decomposed into two relations R1 = (A, C) and R2 = (B, C). Then check if this decomposition dependency preserving or not.

Solution: This can be solved in following steps:

Step 1: For checking whether the decomposition is dependency preserving or not we need to check

following condition

                     F⁺= (F1UF2)⁺    

Step 2: We have with us the F⁺ = { A->B and B->C}

Step 3: Let us find (F1)⁺ for relation R1 and (F2)⁺ for relation R2

Step 4: We will eliminate all the trivial relations and useless relations. Hence we can obtain R1 and R2 as,

(F1UF2)⁺ = {A->C, B->C) ≠ {A->B, B->C) i.e.(F)⁺

Thus the condition specified in step 1 i.e. F⁺=(F1UF2)⁺ is not true. Hence it is not dependency preserving decomposition.

Example 2.10.5 Let relation R(A,B,C,D) be a relational schema with following functional dependencies (A->B, B->C,C->D, and D->B). The decomposition of R into (A,B), (B,C) and (B,D). Check whether this decomposition is dependency preserving or not.

Solution:

Step 1: Let (F) = {A->B, B->C, C->D,D->B}.

Step 2: We will find (F1)⁺, (F2)⁺, (F3)⁺ for relations R1(A,B), R2(B,C) and R3(B,D) as follows -

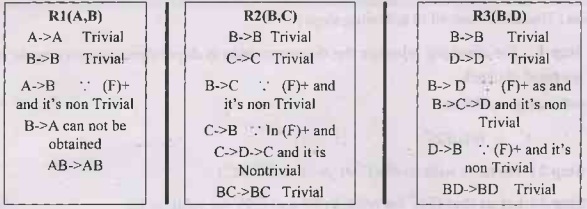
Step 3: We will eliminate all the trivial relations and useless relations. Hence we can obtain R1 U R2 U R3 as,

Step 4: As from above FD's we get

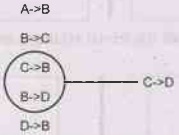
Step 5:This proves that F⁺= (F1UF2UF3)⁺. Hence given decomposition is dependency preserving.

Example 2.10.6 Differentiate lossy decomposition and lossless decomposition.

Solution:

Review questions