Correlation Coefficient for Quantitative Data

Correlation Coefficient for Quantitative Data

• The product moment correlation, r, summarizes the strength of association between two metric (interval or ratio scaled) variables, say X and Y. It is an index used to determine whether a linear or straight-line relationship exists between X and Y.

• As it was originally proposed by Karl Pearson, it is also known as the Pearson correlation coefficient. It is also referred to as simple correlation, bivariate correlation or merely the correlation coefficient.

• The correlation coefficient between two variables will be the same regardless of their underlying units of measurement.

• It measures the nature and strength between two variables of the quantitative type.

• The sign of r denotes the nature of association. While the value of r denotes the strength of association.

• If the sign is positive this means the relation is direct (an increase in one variable is associated with an increase in the other variable and a decrease in one variable is associated with a decrease in the other variable).

• While if the sign is negative this means an inverse or indirect relationship (which means an increase in one variable is associated with a decrease in the other).

• The value of r ranges between (-1) and (+ 1). The value of r denotes the strength of the association as illustrated by the following diagram,

1. If r = Zero this means no association or correlation between the two variables.

2. If 0 < r <0.25 = Weak correlation.

3. If 0.25 ≤ r < 0.75 = Intermediate correlation.

4. If 0.75 ≤ r< 1 = Strong correlation.

5. If r=1= Perfect correlation

• Pearson's 'r' is the most common correlation coefficient. Karl Pearson's Coefficient of Correlation denoted by - 'r' The coefficient of correlation 'r' measure the degree of linear relationship between two variables say x and y.

• Formula for calculating correlation coefficient (r) :

1. When deviation taken from actual mean :

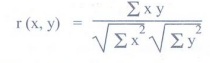
2. When deviation taken from an assumed mean :

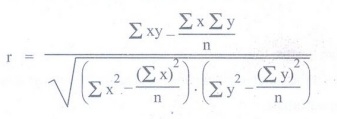
Example 3.3.1: Compute Pearson's coefficient of correlation between maintains cost and sales as per the data given below.

Solution: Given data:

n= 10

X= Maintains cost

y=Sales cost

Calculate coefficient of correlation.

Correlation coefficient is positively correlated.

Example 3.3.2: A random sample of 5 college students is selected and their grades in operating system and software engineering are found to be ?

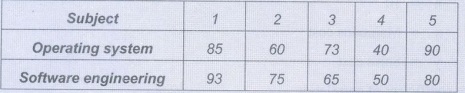
Calculate Pearson's rank correlation coefficient?

Solution:

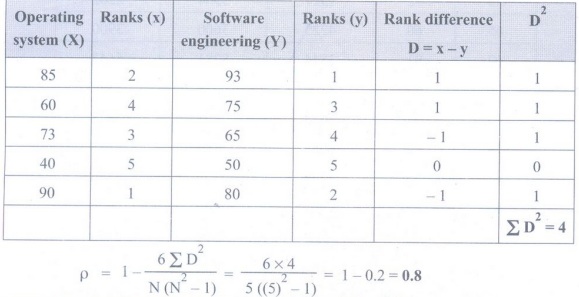
Example 3.3.3: Find Karl Pearson's correlation coefficient for the following paired data.

Solution: Let

x = Wages y = Cost of living

Karl Pearson's correlation coefficient r = 0.847

Example 3.3.4: Find Karl Pearson's correlation coefficient for the following paired data.

What inference would you draw from estimate ?

Solution: