Correlation

UNIT III : Describing Relationships

Syllabus

Correlation - Scatter plots - correlation coefficient for quantitative data - computational formula for correlation coefficient - Regression - regression line - least squares regression line - Standard error of estimate - interpretation of R² - multiple regression equations - regression towards the mean.

Correlation

• When one measurement is made on each observation, uni-variate analysis is applied. If more than one measurement is made on each observation, multivariate analysis is applied. Here we focus on bivariate analysis, where exactly two measurements are made on each observation.

• The two measurements will be called X and Y. Since X and Y are obtained for each observation, the data for one observation is the pair (X, Y).

• Some examples :

1. Height (X) and weight (Y) are measured for each individual in a sample.

2. Stock market valuation (X) and quarterly corporate earnings (Y) are recorded for each company in a sample.

3. A cell culture is treated with varying concentrations of a drug and the growth rate (X) and drug concentrations (Y) are recorded for each trial.

4. Temperature (X) and precipitation (Y) are measured on a given day at a set of weather stations.

•There is difference in bivariate data and two sample data. In two sample data, the X and Y values are not paired and there are not necessarily the same number of X and Y values.

• Correlation refers to a relationship between two or more objects. In statistics, the word correlation refers to the relationship between two variables. Correlation exists between two variables when one of them is related to the other in some way.

• Examples: One variable might be the number of hunters in a region and the other variable could be the deer population. Perhaps as the number of hunters increases, the deer population decreases. This is an example of a negative correlation: As one variable increases, the other decreases.

A positive correlation is where the two variables react in the same way, increasing or decreasing together. Temperature in Celsius and Fahrenheit has a positive correlation.

• The term "correlation" refers to a measure of the strength of association between two variables.

• Covariance is the extent to which a change in one variable corresponds systematically to a change in another. Correlation can be thought of as a standardized covariance.

• The correlation coefficient r is a function of the data, so it really should be called the sample correlation coefficient. The (sample) correlation coefficient r estimates the population correlation coefficient p.

• If either the X, or the Y; values are constant (i.e. all have the same value), then one of the sample standard deviations is zero and therefore the correlation coefficient is not defined.

Types of Correlation

1. Positive and negative

2. Simple and multiple

3. Partial and total

4. Linear and non-linear.

1. Positive and negative

• Positive correlation : Association between variables such that high scores on one variable tends to have high scores on the other variable. A direct relation between the variables.

• Negative correlation : Association between variables such that high scores on one variable tends to have low scores on the other variable. An inverse relation between the variables.

2. Simple and multiple

• Simple: It is about the study of only two variables, the relationship is described as simple correlation.

• Example: Quantity of money and price level, demand and price.

• Multiple: It is about the study of more than two variables simultaneously, the relationship is described as multiple correlations.

• Example: The relationship of price, demand and supply of a commodity.

3. Partial and total correlation

• Partial correlation : Analysis recognizes more than two variables but considers only two variables keeping the other constant. Example: Price and demand, eliminating the supply side.

• Total correlation is based on all the relevant variables, which is normally not feasible. In total correlation, all the facts are taken into account.

4. Linear and non-linear correlation

• Linear correlation : Correlation is said to be linear when the amount of change in one variable tends to bear a constant ratio to the amount of change in the other. The graph of the variables having a linear relationship will form a straight line.

• Non linear correlation : The correlation would be non linear if the amount of change in one variable does not bear a constant ratio to the amount of change in the other variable.

 Classification of correlation

•Two methods are used for finding relationship between variables.

 1. Graphic methods

 2. Mathematical methods.

• Graphic methods contain two sub methods: Scatter diagram and simple graph.

• Types of mathematical methods are,

  a. Karl 'Pearson's coefficient of correlation

  b. Spearman's rank coefficient correlation

  c. Coefficient of concurrent deviation

   d. Method of least squares.

Coefficient of Correlation

Correlation : The degree of relationship between the variables under consideration is measure through the correlation analysis.

• The measure of correlation called the correlation coefficient. The degree of relationship is expressed by coefficient which range from correlation (- 1 ≤ r≥ + 1). The direction of change is indicated by a sign.

• The correlation analysis enables us to have an idea about the degree and direction of the relationship between the two variables under study.

• Correlation is a statistical tool that helps to measure and analyze the degree of relationship between two variables. Correlation analysis deals with the association between two or more variables.

• Correlation denotes the interdependency among the variables for correlating two phenomenon, it is essential that the two phenomenon should have cause-effect relationship and if such relationship does not exist then the two phenomenon can not be correlated.

• If two variables vary in such a way that movement in one are accompanied by movement in other, these variables are called cause and effect relationship.

Properties of Correlation

1. Correlation requires that both variables be quantitative.

2. Positive r indicates positive association between the variables and negative r indicates negative association.

3. The correlation coefficient (r) is always a number between - 1 and + 1.

4. The correlation coefficient (r) is a pure number without units.

5. The correlation coefficient measures clustering about a line, but only relative to the SD's.

6. The correlation can be misleading in the presence of outliers or nonlinear association.

7. Correlation measures association. But association does not necessarily show causation.

 Example 3.1.1: A sample of 6 children was selected, data about their age in years and weight in kilograms was recorded as shown in the following table. It is required to find the correlation between age and weight.

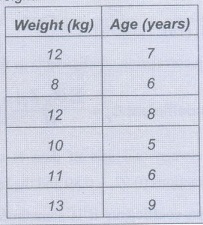
Solution :

X = Variable age is the independent variable

Y = Variable weight is the dependent

• Other formula for calculating correlation coefficient is as follows:

Interpreting the correlation coefficient C_r = Σ (Z_x Z_y)/N

•Because the relationship between two sets of data is seldom perfect, the majority of correlation coefficients are fractions (0.92, -0.80 and the like).

• When interpreting correlation coefficients it is sometimes difficult to determine what is high, low and average.

• The value of correlation coefficient 'r' ranges from - 1 to +1.

• If r = + 1, then the correlation between the two variables is said to be perfect and positive.

•If r = -1, then the correlation between the two variables is said to be perfect and negative.

• If r = 0, then there exists no correlation between the variables.

Example 3.1.2: A sample of 12 fathers and their elder sons gave the following data about their heights in inches. Calculate the coefficient of rank correlation.

Solution:

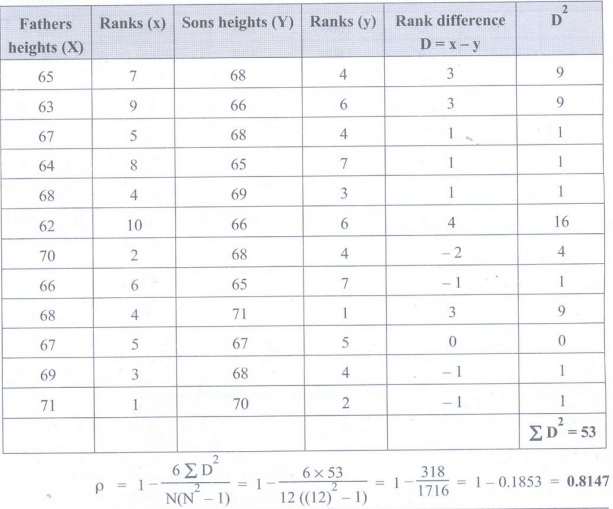
Example 3.1.3: Calculate coefficient of correlation between age of cars and annual maintenance and comment.

Solution: Let,

x = Age of cars y= Annual maintenance cost, n = 7

Calculate X̄ = 2+4+6+ 7+ 8+10+12 / 7 = 49/7= 7

Calculate Ȳ = 1600+ 1500+ 1800+ 1900+ 1700 + 2100 + 2000 /7

= 12600 / 7 = 1800

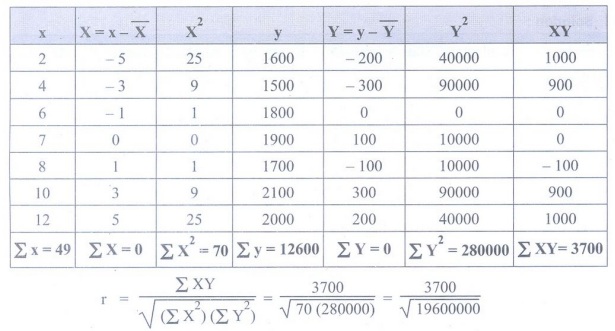
=3700/4427.188 = 0.8357

Coefficient of correlation r = 0.8357

Example 3.1.4: Calculate coefficient of correlation from the following data.

Solution: In the problem statement, both series items are in small numbers. So there is no need to take deviations.

Computation of coefficient of correlation

= 46 / 5.29 × 9.165

r = 0.9488