Boyce / Codd Normal Form (BCNF)

Boyce / Codd Normal Form (BCNF)

Boyce and Codd Normal Form is a higher version of the Third Normal form. This form deals with certain type of anomaly that is not handled by 3NF.

A 3NF table which does not have multiple overlapping candidate keys is said to be in BCNF.

Or in other words,

For a table to be in BCNF, following conditions must be satisfied:

i) R must be in 3rd Normal Form

ii) For each functional dependency (X → Y), X should be a super Key. In simple words if Y is a prime attribute then X can not be non prime attribute.

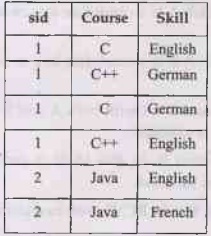
For example - Consider following table that represents that a Student enrollment for the course -

Enrollment Table

From above table following observations can be made:

• One student can enroll for multiple courses. For example student with sid=1 can enroll for C as well as Java.

• For each course, a teacher is assigned to the student.

• There can be multiple teachers teaching one course for example course C can be taught by both the teachers namely - Ankita and Archana.

• The candidate key for above table can be (sid,course), because using these two columns we can find

• The above table holds following dependencies,

     • (sid,course)->Teacher

     • Teacher->courseann

• The above table is not in BCNF because of the dependency teacher->course. Note NS that the teacher is not a superkey or in other words, teacher is a non prime attribute and course is a prime attribute and non-prime attribute derives the prime attribute.

• To convert the above table to BCNF we must decompose above table into Student and Course tables

Student

Course

Now the table is in BCNF

Example 2.12.1 Consider a relation(A,B,C,D) having following FDs.(AB->C, AB->D, C->A, B->D). Find out the normal form of R.

Solution:

Step 1: We will first find out the candidate key from the given FD.

(AB)⁺= {ABCD) = R

(BC)⁺={ABCD) = R

(AC)⁺ ={AC} R

There is no involvement of D on LHS of the FD rules. Hence D can not be part of any candidate key. Thus we obtain two candidate keys (AB)* and (BC)*. Hence

prime attributes = {A,B,C)

Non prime attributes = {D}

Step 2: Now, we will start checking from reverse manner, that means from BCNF, so then 3NF, then 2NF.

Step 3: For R being in BCNF for X->Y the X should be candidate key or super key. From above FDs consider C->D in which C is not a candidate key or super key. Inabu Hence given relation is not in BCNF.

Step 4: For R being in 3NF for X->Y either i) the X should be candidate key or super key or ii) Y should be prime attribute. (For prime and non prime attributes refer step 1)

  • For AB->C or AB->D the AB is a candidate key. Condition for 3NF is satisfied.

  • Consider C->A. In this FD the C is not candidate key but A is a prime attribute. Condition for 3NF is satisfied.

  • Now consider B->D. In this FD, the B is not candidate key, similarly D is not a prime attribute. Hence condition for 3NF fails over here.

Hence given relation is not in 3NF.

Step 5: For R being in 2NF following condition should not occur.

Let X->Y, if X is a proper subset of candidate key and Y is a non prime attribute. This is a case of partial functional dependency.

For relation to be in 2NF there should not be any partial functional dependency.

  • For AB->C or AB->D the AB is a complete candidate key. Condition for 2NF is satisfied.

  • Consider C->A. In this FD the C is not candidate key. Condition for 2NF is satisfied.

  • Now consider B->D. In this FD, the B is a part of candidate key(AB or BC), similarly D is not a prime attribute. That means partial functional dependency occurs here. Hence condition for 2NF fails over here.

Hence given relation is not in 2NF.

Therefore we can conclude that the given relation R is in 1NF.

Example 2.12.2 Consider a relation R(ABC) with following FD A->B, B->C and C->A. What is the normal form of R?

Solution:

Step 1: We will find the candidate key

(A)⁺ ={ABC} =R

(B)⁺ = {ABC} =R

(C)⁺={ABC} =R

Hence A, B and C all are candidate keys

Prime attributes = {A,B,C}

Non prime attribute {}

Step 2:For R being in BCNF for X->Y the X should be candidate key or super key. From above FDs

  • Consider A->B in which A is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider B->C in which B is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider C->A in which C is a candidate key or super key. Condition forBCNF is satisfied.

This shows that the given relation R is in BCNF.

Example 2.12.3 Prove that any relational schema with two attributes is in BCNF.

Solution: Here, we will consider R={A,B) i.e. a relational schema with two attributes. Now various possible FDs are A->B, B->A.

From the above FDs

  • Consider A->B in which A is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider B->A in which B is a candidate key or super key. Condition for BCNF is satisfied.

  • Consider both A->B and B->A with both A and B is candidate key or super key. Condition for BCNF is satisfied.

  • No FD holds in relation R. In this {A,B) is candidate key or super key. Still condition for BCNF is satisfied.

This shows that any relation R is in BCNF with two attributes.