Bi-Connectivity

Bi-Connectivity

Biconnected graphs are the graphs which can not be broken into two disconnected pieces (graphs) by connecting single edge. For example :

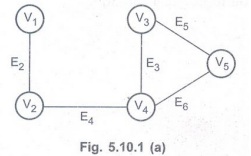
In the given Fig. 5.10.1 (a) even if we remove any single edge the graph does not become disconnected.

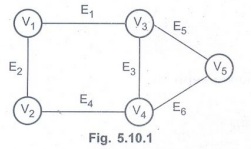
For example even if we remove an edge E1 the graph does not become disconnected. We do not get two disconnected components of graph. Same is the case with any other edge in the given graph.

But the following graph does not possess the property of Biconnectivity.

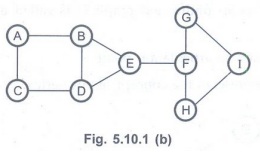
In above graph if we remove an edge E-F then we will get two distinct graphs.

Properties of Biconnected Graph:

1. There are two disjoint paths between any two vertices.

2.There exists simple cycle between two vertices.

3. There should not be any cut vertex (Cut vertex is a vertex which if we remove then the graph becomes disconnected.)

Strongly Connected Components

Strongly Connectivity Definition :

A directed graph is strongly connected if there is directed path from any vertex to every other vertex.

The connected components are called strongly connected components for example:

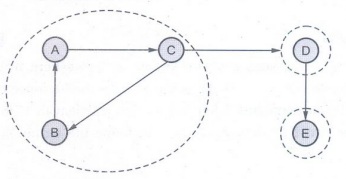
In above graph the strongly connected components are represented by dotted marking.

Review Questions

1. Write short notes on biconnectivity.

2. Explain in detail about strongly connected components and illustrate with an example.