B-Tree

UNIT IV

CHAPTER 5 : Multiway Search Trees and Graphs

Part I: Multiway Trees

B-Tree

B-tree is a specialized multiway tree used to store the records in a disk. There are number of subtrees to each node. So that the height of the tree is relatively small. So that only small number of nodes must be read from disk to retrieve an item. The goal of B-trees is to get fast access of the data.

Multiway search tree

B-tree is a multiway search tree of order m is an ordered tree where each node has at the most m children. If there are n number of children in a node then (n - 1) is the number of keys in the node.

For example:

Following is a tree of order 4.

From above tree following observations can be made

1. The node which has n children posses (n - 1) keys.

2. The keys in each node are in ascending order.

3. For every node Node.child [0] has only keys which are less then Node.key [0] similarly, Node.child [1] has only keys which are greater than Node.key [0]

In other words, the node at level 1 has F, K and O as keys. At level 2 the node containing. keys C and D are arranged as child of key F (the cell before F). Similarly the node containing key G will be child of F but should be attached after F and before K, as G is between F and K. Here the alphabets F, K, O are called keys and branches are called children. The B-tree of order m should be constructed using following properties.

Rule 1:

All the leaf nodes are on the botom level.

Rule 2:

The root node should have at least two children.

Rule3;

All the internal nodes except root node have at least ceil (m/2) nonempty children. The ceil is a function such that ceil (3.4) = 4, ceil (9.3) = 10, ceil (2.98) = 3 ceil (7) = 7.

Rule 4;

Each leaf node must contain at least ceil (m/2) - 1 keys.

Insertion    

Thus the B-tree is fairly balanced tree which can be illustrated by following example.

Example of B-tree

We will consruct a B-tree of order 5 following numbers.

3, 14, 7, 1, 8, 5, 11, 17, 13, 6, 23, 12, 20, 26, 4, 16, 18, 24, 25, 19.

The order 5 means at the most 4 keys are allowed. The internal node should have at least 3 nonempty children and each leaf node must contain at least 2 keys..

Step 1: Insert 3, 14, 7, 1 as follows.

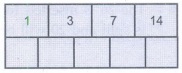
Step 2: If we insert 8 then we need to split the node 1, 3, 7, 8, 14 at medium.

Step 3: Insert 5, 11, 7 which can be easily inserted in a B-tree.

Step 4 :

Now insert 13. But if we insert 13 then the leaf node will have 5 keys which is not allowed. Hence 8, 11,13, 14, 17 is split and medium node 13 is moved up.

Step 5:

Now insert 6, 23, 12, 20 without any split.

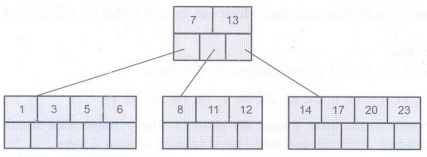
Step 6: The 26 is inserted to the rightmost leaf node. Hence 14, 17, 20, 23, 26 the node is split and 20 will be moved up.

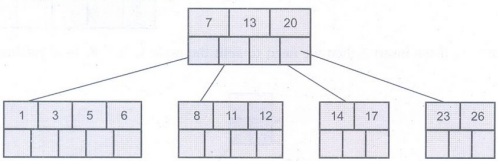
Step 7: Insertion of node 4 causes left most node to split. The 1, 3, 4, 5, 6 causes key 4 to move up. Then insert 16, 18, 24, 25.

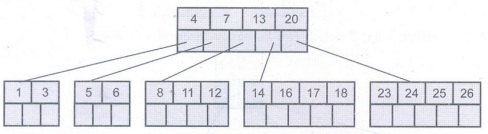
Step 8: Finally insert 19. Then 4, 7, 13, 19, 20 needs to be split. The median 13 will be moved up to form a root node.

The tree then will be -

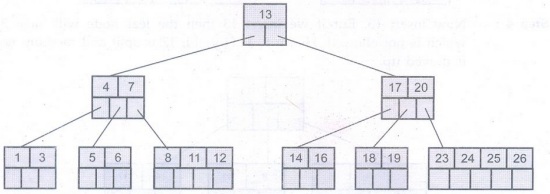
Thus the B-tree is constructed.

Ex. 5.1.1 Distinguish between B Tree and B+ Tree. Create a B three of order 5 by inserting the following elements: 3,14,7,1,8,5,11,17,13,6,23,12,20,26,4,16,18,24,25 and 19.

Sol. :

Example: Creation of B tree - Refer section 5.1.1.

Algorithm for insertion in B-tree

Algorithm insert (root, key)

{

// Problem Description: This algorithm is for

// inserting key node in B-tree.

temp ←root

if (n[temp]=2t 1) then

s←get_node () // memory is allocated.

{

roots←s

leaf [s] ←FALSE

n [s] ←0

child1[s] ←root

split_child (s, 1, root)

Insert_In (s, key)

}

Else

Insert_In (s, key)

}

Deletion

Consider a B-tree

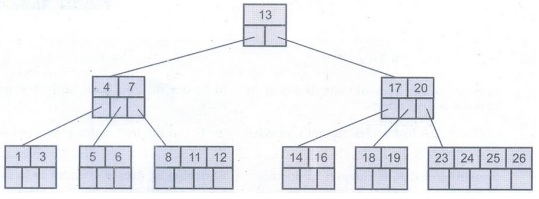
If we want to delete 8 then it is very simple

Now we will delete 20, the 20 is not in a leaf node so we will find its successor which is 23. Hence 23 will be moved up to replace 20.

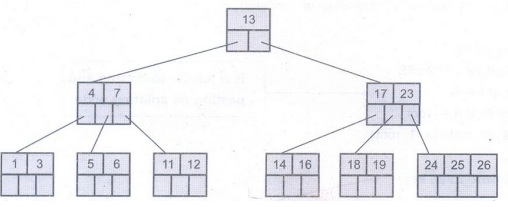
Next we will delete 18. Deletion of 18 from the corresponding node causes the node with only one key, which is not desired (as per rule 4) in B-tree of order 5. The sibling node to immediate right has an extra key. In such a case we can borrow a key from parent and move spare key of sibling to up. See the following figure.

Now delete 5. But deletion of 5 is not easy. The first thing is 5 is from leaf node. Secondly this leaf node has no extra keys nor siblings to immediate left or right. In such a situation we can combine this node with one of the siblings. That means remove 5 and combine 6 with the node 1, 3. To make the tree balanced we have to move parent's key down. Hence we will move 4 down as 4 is between 1, 3 and 6. The tree will be

But again internal node of 7 contains only one key which not allowed in B-tree (as per rule 3). We then will try to borrow a key from sibling. But sibling 17, 24 has no spare key. Hence what we can do is that, combine 7 with 13 and 17, 24. Hence the B-tree will be

Ex. 5.1.2: Construct a B-tree with order m = 3 for the key values 2,3,7,9,5,6,4,8,1 and delete the values 4 and 6. Show the tree in performing all operations.

Sol. The order m = 3 means at the most 2 keys are allowed. The insertion operation is as follows:

Step 6: Insert 4. This will make a sequence 4,5, 6. The 5 will go up. Then the sequence will become 3,5, 7. Again 5 will go up.

Step 8; Delete 4 and 6. As these are the leaf nodes without any adjacent key. Their deletion is very simple. Just make these node as NULL. The remaining adjustment will occur. The resultant B-tree will be,

Searching

The search operation on B-tree is similar to a search on binary search tree. Instead of choosing between a left and right child as in binary tree, B-tree makes an m-way choice. Consider a B-tree as given below

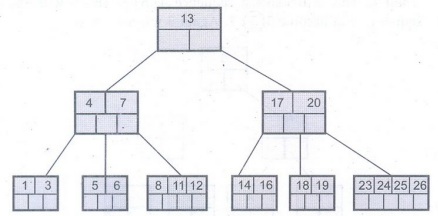
If we want to search node 11 then

i) 11 13 Hence search left node

ii) 11 > 7: Hence rightmost node

iii) 11 > 8, move in second block

iv) node 11 is found.

The running time of search operation depends upon the height of the tree. It is O(log n).

Algorithm

The algorithm for searching a target node is as follows

Algorithm Search (temp, target)

{

// Problem Description: This algorithm is for

// searching the 'target' node

i ←1

while i←i + 1 ((i≤n[temp]) AND (target > key; [temp]))

if ((i≤n[temp]) AND (target ==key.[temp]))

return (temp, i)

if (leaf [temp]==TRUE) then

return NULL

else READ (C_i [temp])

return search ((C_i [temp], target)

}

The search operation on B-tree is similar to a search operation on a binary tree. The desired child is chosen by performing linear search of values in the node. The running time of this algorithm is O(log n).

Height of B-Tree

The maximum height of B-tree gives an upper bound on number of disk access. The minimum number of keys in a B-tree of order 2m and depth h is

1 + 2m + 2m(m + 1) + 2m(m+1)² + ... +2m(m+1)^h-1

The maximum height of B-tree with n keys

log_m+1 n/ 2m = O(log_n)

Review Questions

1. Explain the properties of B-trees.

2. Explain the insertion and deletion of nodes in the B-trees with suitable example.

3. What is a B-tree? Mention the properties that a B-tree holds.