Two Marks Questions with Answers

Two Marks Questions with Answers

Q.1 List any four ways of theorem proving.

Ans. : 1) Proof by contradiction.

2) Proof by contrapositive.

3) Proof by counter example.

4) Proof by principle of mathematical induction.

Q.2 Differentiate between proof by contradiction and proof by contrapositive.  AU: May-11

Ans. The difference between proof by contradiction and contrapositive

Q.3 Define automata.

Ans.: Automata are the kind of machines which take some string as input. This input goes through a finite number of states and may enter in the final state.

Q.4 List the applications of automata theory.

Ans.: 1. Automata theory is the base for the formal languages and these formal languages are useful of the programming languages.

2. Automata theory plays an important role in compiler design.

3. To prove the correctness of the program automata theory is used.

4. In switching theory and design and analysis of digital circuits automata theory is applied.

5. Automata theory deals with the design finite state machines.

Q.5 What is structural induction? AU: Dec.-11

Ans.: Structural induction is a kind of proof by induction. It is used to prove that there exists a relationship between some function of integers and a given formula. For this proof technique -

1. Prove the pattern is true for smallest number we care about.

2. Assume it holds for an arbitrary number n.

3. Prove that if it is true for n, then it must be true for n + 1, as well.

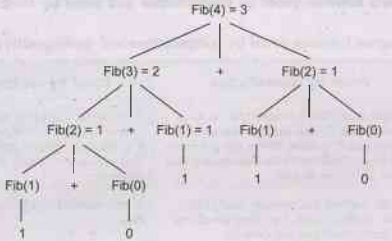
Q.6 How does recursive function solves Fibonacci function ?

Ans.: Following recursive formula is used to solve Fibonacci function.

Fib(n) = Fib(n - 1) + Fib(n - 2)

Fib(0) = 0 and Fib(1) = 1

For example, to compute Fib(4)

Q.7 What is induction principle? Give an example. AU: Dec.-12

Ans.: The proof by mathematical induction can be carried out using following steps –

1. Basis: In this step we assume the lowest possible value. This is an initial step in the proof of mathematical induction.

For example, we can prove that the result is true for n = 0 or n = 1.

2. Induction Hypothesis: In this step we assign value of n to some other value k. That mean we will check whether the result is true for n = k or not.

3. Inductive Step: In this step, if n = k is true then we check whether the result is true for n k+ 1 or not. If we get the same result at n = k + 1 then we can state that given proof is true by principle of mathematical induction.

Q.8 What is the proof by contradiction? AU: May-12

Ans.: In proof by contradiction technique, for the statement of the form if A then B we start with statement A is not true and thus by assuming this false A we try to get the conclusion of statement B. When it becomes impossible to reach to statement B, then we contradict ourselves and accept that A is true.

Q.9 Define NFA with ε transition. Is the NFA's with ε transitions more powerful than the NFA's without ε transitions? AU: May-05, 18

Ans.: The NFA can be formally defined as a collection of 5 tuples.

Q is a finite set of states.

Σ is a finite set of inputs.

δ is called next state or transition function.

q₀ is initial state.

F is a final state where F Q.

No. The NFA with e transitions are equivalent to the NFA without ε transitions.

Q.10 Construct a finite automata for the language {0ⁿ | n mod 3 = 2, n ≥ 0}. AU: Dec.-06

Ans.: While testing divisibility by 3 we group the input as

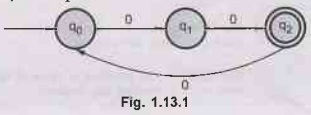
q₀ remainder 0 state.

q₁ remainder 1 state.

q₂ remainder 2 state.

The q₂ is remainder 2 state hence we will make it as final state.

Q.11 What is a finite automation? Give two examples.  AU: May-07, Dec.-15, 17

Ans.: A finite automation is a collection of 5-tuples (Q, Σ, δ, q₀, F) where

• Q is a finite set of states, which is a non-empty one.

• Σ is input alphabet, indicates input set.

• q₀ in Q is the initial state.

• F is a set of final states.

• δ is a transition function.

For example -

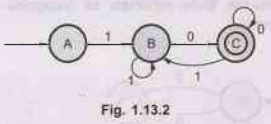
1. The FA which accepts only those strings which start with 1 and end with 0.

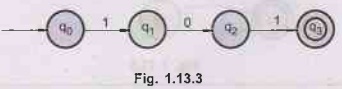
2. The FA which accepts the only input 101.

Q.12 Enumerate the differences between DFA and NFA.  AU: May-07,14, Dec.-17, 18

Ans. :

Q.13 Construct a DFA over Σ = (a, b) which produces not more than 3a's. AU: May-08

Ans.: In the given language at the most 3a's are allowed and there is no restriction on number of b's. Such a DFA can be as shown in Fig. 1.13.4.

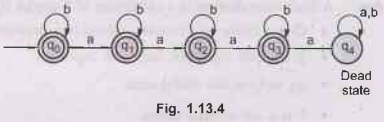
The above DFA accepts {ε, a, aa, aaa, ab, aba,...}. The states q₀, q₁, q₂ and q₃ are final states but state q₄ is a non-final state. Thus the above DFA accepts 3a's and not more than that.

Q.14 Define the languages described by NFA and DFA.  AU: Dec.-08

[Refer sections 1.6 and 1.7

• The finite automata is called Deterministic Finite Automata if there is only one path for a specific input from current state to next state. For example, the DFA can be shown in Fig. 1.6.1.

• The concept of Non-deterministic Finite Automata is exactly reverse of Deterministic Finite Automata. The Finite Automata is called NFA when there exists many paths for a specific input from current state to next state. The NFA can be shown as in Fig. 1.7.1

Q.15 Construct deterministic finite automata to recognise odd number of 1's and even number of zero's. AU: May-10

Ans. :

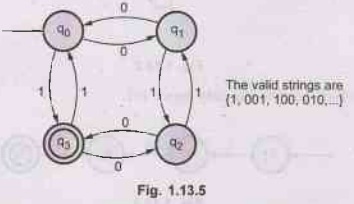
Q.16 Construct a DFA for the language over {0, 1}* such that it contains "000" as a substring.  AU : May-11

Ans.:

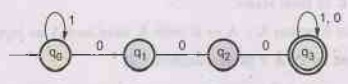
Q.17 Construct a DFA for the following:

a) All strings that contain exactly 4 - zeros.

b) All strings that don't contain the substring 110.  AU: Dec.-11

Ans. a) The DFA will be

b) For required DFA, we will first create a DFA that contains the substring 110.

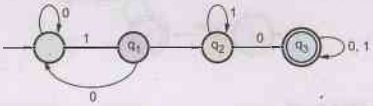
Now change non-final state to final state and final state to non-final state.

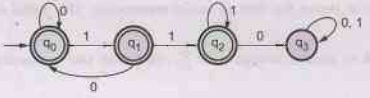
Q.18 Find the set of strings accepted by the finite automata. AU: Dec.-10

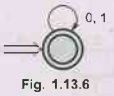
Ans.: Set of strings accepted by given finite automata are

S = {ε, 0, 1, 00, 000, 11, 111, 01, 10, 101, 110, 001, ...)

Q.19 Define a) Finite Automaton (FA) b) Transition diagram. AU: Dec.-12

Ans.: a) Finite Automaton (FA): Refer answer of Q.11.

Ans.: A finite automation is a collection of 5-tuples (Q, Σ, δ, q₀, F) where

• Q is a finite set of states, which is a non-empty one.

• Σ is input alphabet, indicates input set.

• q₀ in Q is the initial state.

• F is a set of final states.

• δ is a transition function.

b) Transition diagram: A transition diagram can be defined as collection of -

1) Finite set of states K

2) Finite set of symbols

3) A non empty set S of K which is called start state.

4) A set F  K of final states.

5) A transition function K × A → K with K state and A as input from Σ*.

Q.20 What is meant by DFA ? [Refer section 1.6] AU: May-13

The finite automata is called Deterministic Finite Automata if there is only one path for a specific input from current state to next state. For example, the DFA can be shown in Fig. 1.6.1.

From state S0 for input 'a' there is only one path, going to S2. Similarly from S0 there is only one path for input b going to S1.

The DFA can be represented by the same 5-tuples described in the definition of FSM.

Q.21 Define the term epsilon transition. AU: May-13

Ans.: In the non deterministic finite state machine, the transition that does not require input symbols for state transition and is capable of transiting to zero or more states with & is called epsilon transition.

Q.22 What is a non deterministic finite automation? [Refer section 1.7]  AU: Dec.-13

 • The concept of Non-deterministic Finite Automata is exactly reverse of Deterministic Finite Automata. The Finite Automata is called NFA when there exists many paths for a specific input from current state to next state. The NFA can be shown as in Fig. 1.7.1

• Note that the NFA shows from q0 for input a there are two next states q1 and q2. Similarly, from q0 for input b the next states are q0 and q1.

• Thus it is not fixed or determined that Fig. 1.7.1 Non-deterministic finite automata with a particular input where to go next. Hence this FA is called non-deterministic finite automata.

Q.23 Draw the transition diagram (automata) for an identifier. AU: Dec.-13

Ans. :

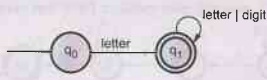
Q.24 Define deductive proof. AU Nov.-14

Ans.: The deductive proof consists of sequence of statements given with logical reasoning in order to prove the first or initial statements. The initial statement is called hypothesis.

Q.25 Design DFA to accept strings over Σ = (0,1) with two consective O's. AU: Nov.-14

Ans.:

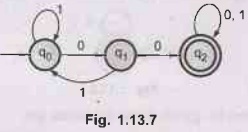
Q.26 Define Deterministic Finite Automata (DFA). AU: Dec.-16,19

Ans.:

The Deterministic Finite Automata is a collection of following things:

1) Finite set of states - Q

2) Finite set of input symbols - Σ

3) The start state q₀ such that q₀ ϵ Q.

4) The set of final states F such that F ϵ Q

5) The mapping function δ.

The DFA is denoted by,

M = (Q, Σ, δ, q₀, F).

Q.27 Draw a non-deterministic automata to accept a string containing substring 0101. AU: May-16

Ans.:

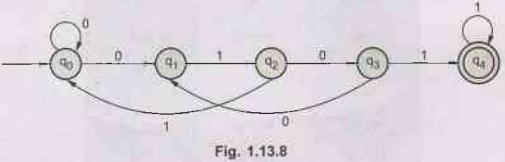
Q.28 Obtain the DFA equivalent to the following NFA. AU: Dec.-03

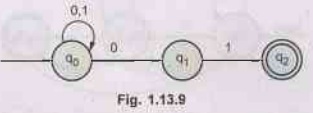
Ans.: The transition table for given NFA can be drawn as follows.

To construct equivalent DFA.

δ (q₀, 0) = {q₀, q₁} a new state

δ {q₀, 1} = {q₀}

δ {q₁, 1) = -

δ (q₁, 1} = {q₂}

δ {q₂, 0} = -

δ {q₂, 1} = -

δ {{q₀, q₁), 0} = {q₀, q₁}

δ {{q₀, q₁), 1} = {q₀, q₂} a new state

δ {{q₀, q₂}, 0} = {q₀, q₁}

δ {{q₀, q₂}, 1} = {q₀}

Hence the DFA is

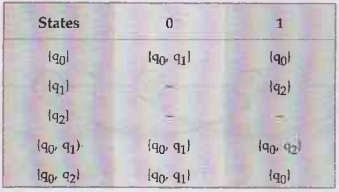
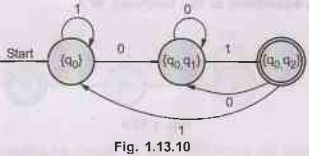
The transition diagram can be drawn as follows.

Q.29 Obtain the NFA without ε transition to the following NFA with ε transition. AU: Dec.-03

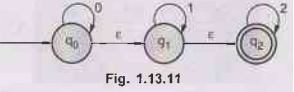
Ans.: Remove ε transition from q₀ to q₁.

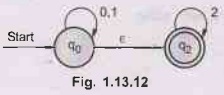
Now remove ε transition from q₀ to q₂.

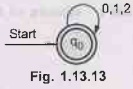
As q₀ to q₂ is ε transition q₀ will become start and final state both.

Q.30 Obtain the ε - closure of states q₀ and q₁ in the following NFA with ε transition. AU: Dec.-04

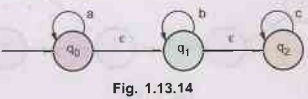
Ans.: ε - closure {q₀} = {q₀, q₁, q₂}

ε - closure {q₁} = {q₁, q₂}

These are ε - reachable states from q₀ and q₁.

Q.31 Obtain ε - closure of each state in the following NFA with ε move. AU: Dec.-05

Ans.: The ε - closure of each state means collection of ε - reachable states.

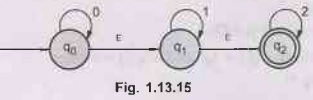
ε - closure (q₀) = {q₀, q₁, q₂} as we have ε transition from q₀ to q₀, q₁, q₂.

ε - closure (q₁) = {q₁, q₂}

ε - closure {q₂} = {q₂}

Q.32 Find the language accepted by the DFA given below. AU: May-06

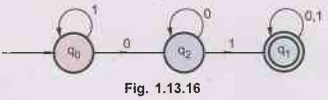
Ans.: The regular expression for this DFA is

r.e. = 1*00*1 (0+1)*

= 1*0*1 (0+1)*

That means this is a language containing all the strings which consist of atleast one single pair of 01.

Q.33 Find the closure of the states 1, 2 and 4 in the following transition diagram.  AU: May-06

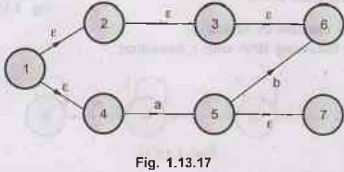
Ans.: ε - closure {1} = {1, 2, 3, 6, 4}

ε - closure {2} = {2, 3, 6}

ε - closure {4} = {4}

Q.34 Define ε - closure.

Ans.: The ε - closure (p) is a set of all states which are reachable from state p on ε - transitions such that:

i) ε - closure (p) = p where p ϵ Q.

ii) If there exists ε - closure (p) = {q} and δ (q, ε) = r then

ε - closure (p) = {q, r}

Q.35 Define ε - closure (q) with an example. AU: May-12

Ans. Definition: Refer answer of Q.34.

Ans.: The ε - closure (p) is a set of all states which are reachable from state p on ε - transitions such that:

i) ε - closure (p) = p where p ϵ Q.

ii) If there exists ε - closure (p) = {q} and δ (q, ε) = r then

ε - closure (p) = {q, r}

Example: Refer answer of Q.31.

Ans.: The ε - closure of each state means collection of ε - reachable states.

ε - closure (q₀) = {q₀, q₁, q₂} as we have ε transition from q₀ to q₀, q₁, q₂.

ε - closure (q₁) = {q₁, q₂}

ε - closure {q₂} = {q₂}