Tree Traversal

Tree Traversal

• Definition: Tree traversal means visiting each node exactly once.

•Basically there are six ways to traverse a tree. For these traversals we will use following notations :

L for moving to left child

R for moving to right child

D for parent node

• Thus with L, R, D we will have six combinations such as LDR, LRD, DLR, DRL, RLD, RDL.

• From computation point of view, we will consider only three combinations as LDR, DLR and LRD i.e. inorder, preorder and postorder respectively.

1) Inorder Traversal :

In this type of traversal, the left node is visited, then parent node and then right node is visited.

For example

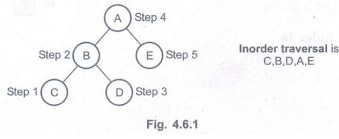
Algorithm:

1. If tree is not empty then

a. traverse the left subtree in inorder

b. visit the root node

c. traverse the right subtree in inorder

The recursive routine for inorder traversal is as given below to

void inorder(node *temp)

{

if(temp!= NULL)

{

inorder(temp->left);

printf("%d",temp->data);

inorder(temp->right);

}

}

2) Preorder Traversal :

In this type of traversal, the parent node or root node is visited first; then left node and finally right node will be visited.

For example

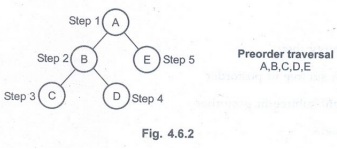
Algorithm:

1.   If tree is not empty then

     a. visit the root node

     b. traverse the left subtree in preorder

    c. traverse the right subtree in preorder

The recursive routine for preorder traversal is as given below.

void preorder(node *temp)

{

if(temp!= NULL)

{

printf("%d",temp->data);

preorder(temp->left);

preorder(temp->right);

}

}

3) Postorder Traversal :

In this type of traversal, the left node is visited first, then right node and finally parent node is visited.

For example

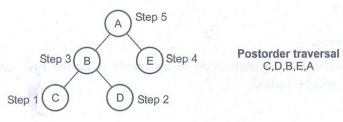
Algorithm:

1. If tree is not empty then

a. traverse the left subtree in postorder

b. traverse the right subtree in postorder

c. visit the root node

The recursive routine for postorder traversal is as given below.

void postorder(node *temp)

{

if(temp!= NULL)

{

postorder(temp->left);

postorder(temp->right);

printf("%d",temp->data);

}

}

Ex. 4.6.1: Write inorder, preorder and postorder traversal for the following tree:

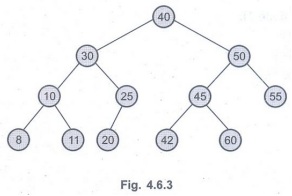
Sol. :

Inorder 8 10 11 30 20 25 40 42 45 60 50 55

Preorder 40 30 10 8 11 25 20 50 45 42 60 55

Postorder 8 11 10 20 25 30 42 60 45 55 50 40.

Ex. 4.6.2. Implementation of binary tree

Sol. : /***************************************************************

Program for creation of a binary tree and display the tree using recursive inorder, preorder and post order traversals

****************************************************************/

#include <stdio.h>

#include <alloc.h>

#include<conio.h>

typedef struct bin

{

int data;

struct bin *left;

struct bin *right;

}node;/*Binary tree structure*/

void insert(node *, node *);

void inorder(node *);

void preorder(node *);

void postorder(node *);

node *get_node();

void main()

{

int choice;

char ans='n';

node *New,*root;

root=NULL;

clrscr();

do

{

printf("\n Program For Implementing Simple Binary Tree");

printf("\n 1.Create");

printf("\n 2.Inorder");

printf("\n 3.Preorder ");

printf("\n 4.Postorder");

printf("\n 5.Exit");

printf("\n\t Enter Your Choice: ");

scanf("%d", &choice);

switch(choice)

{

case 1:root = NULL;

do

{

New get_node();

printf("\n Enter The Element: ");

scanf("%d", &New->data);

if(root == NULL)

root=New;

else

insert(root,New);

printf("\n Do You want To Enter More elements?(y/n):");

ans=getche();

} while (ans=='y' || ans == 'Y');

clrscr();

break;

case 2:if(root == NULL)

printf("Tree Is not Created!");

else

inorder(root);

break;

case 3:if(root == NULL)

printf("Tree Is Not Created!");

else

preorder(root);

break;

case 4:if(root == NULL)

printf("Tree Is Not Created!");

else

postorder(root);

break;

}

}while(choice!=5);

}

node *get_node()

{

node *temp;

temp=(node *)malloc(sizeof(node));

temp->left = NULL;

temp->right= NULL;

return temp;

}

void insert(node *root,node *New)

{

char ch;

printf("\n Where to insert left/right of %d: ", root->data);

ch=getche();

if ((ch=='r') || (ch=='R'))

{

if(root->right== NULL)

{

root->right=New;

}

else

insert(root->right,New);

}

else

{

if (root->left== NULL)

{

root->left=New;

}

else

insert(root->left, New);

}

}

void inorder(node *temp)

{

if(temp!= NULL)

{

inorder(temp->left);

printf("%d",temp->data);

inorder(temp->right);

}

}

void preorder(node *temp)

{

if(temp!= NULL)

{

printf("%d",temp->data);

preorder(temp->left);

 preorder(temp->right);

}

}

void postorder(node *temp)

{

if(temp!= NULL)

{

postorder(temp->left);

postorder(temp->right);

printf("%d",temp->data);

}

}

Output

Program For Implementing Simple Binary Tree

1.Create

2.Inorder

3.Preorder

4.Postorder

5.Exit

Enter Your Choice: 1

Enter The Element: 10

Do You Want To Enter More Elements?(y/n): y

Enter The Element: 12

Where to insert left/right of 10: 1

Do You Want To Enter More Elements?(y/n): y

Enter The Element: 17

Where to insert left/right of 10: r

Do You Want To Enter More Elements?(y/n): y

Enter The Element: 8

Where to insert left/right of 10:1

Where to insert left/right of 12: r

Do You Want To Enter More Elements?(y/n):

Program For Implementing Simple Binary Tree

 1.Create

2.Inorder

3.Preorder

4.Postorder

5.Exit

Enter Your Choice: 2

12 8 10 17

Program For Implementing Simple Binary Tree

1.Create

2.Inorder

3.Preorder

4.Postorder

5.Exit

Enter Your Choice: 3

10 12 8 17

Program For Implementing Simple Binary Tree

1.Create

2.Inorder

3.Preorder

4.Postorder

5.Exit

Enter Your Choice: 4

8 12 17 10

Program For Implementing Simple Binary Tree

1. Create

2. Inorder

3. Preorder

4. Postorder

5. Exit

Enter Your Choice: 5

Review Question

1. Explain the tree traversal techniques with an example.