Programming in C: Unit III (a): Functions
Tower of Hanoi (recursion)
with Example C Programs | Functions
The tower of Hanoi is one of the main applications of recursion. It says, 'if you can solve n-1 cases, then you can easily solve the nth case'.
TOWER
OF HANOI
The
tower of Hanoi is one of the main applications of recursion. It says, 'if you
can solve n-1 cases, then you can
easily solve the nth case'.
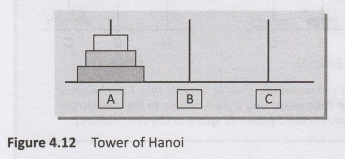
Look
at Figure 4.12 which shows three rings mounted on pole A. The problem is to
move all these rings from pole A to pole C while maintaining the same order.
The main issue is that the smaller disk must always come above the larger disk.
We
will be doing this using a spare pole. In our case, A is the source pole, C is
the destination pole, and B is the spare pole. To transfer all the three rings
from A to C, we will first shift the upper two rings (n-1 rings) from the
source pole to the spare pole. We move the first two rings from pole A to B as
shown in Figure 4.13.
Now
that n-1 rings have been removed from
pole A, the nth ring can be easily moved from the source pole (A) to
the destination pole (C). Figure 4.14 shows this step. The final step is to
move the n-1 rings from B to C using
A as the spare pole. This is shown in Figure 4.15.
To
summarize, the solution to our problem of moving n rings from A to C using B as
spare can be given as:
Base case:
if n=1
•
Move the ring from A to C using B as spare
Recursive case:
•
Move n-1 rings from A to B using C as spare
•
Move the one ring left on A to C using B as spare
•
Move n-1 rings from B to C using A as spare
The
following code implements the solution of the Tower of Hanoi problem.
#include <stdio.h>
void move (int, char, char, char);
int main()
{
int n;
printf("\n Enter the number of
rings: ");
scanf("%d", &n);
move (n, 'A', 'C', 'B');
return 0;
}
void move (int n, char source, char
dest, char (spare)
{
if (n==1)
printf("\n Move from %c to %c",
source, dest);
else
{
move (n-1, source, spare, dest);
move (1, source, dest, spare);
move (n-1, spare, dest, source);
}
}
Let us look at the
Tower of Hanoi problem in detail using the program given above. Figure 4.16
explains the working of the program using one, then two, and finally three
rings.
Programming in C: Unit III (a): Functions : Tag: : with Example C Programs | Functions - Tower of Hanoi (recursion)
Programming in C: Unit III (a): Functions
Under Subject
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation