The Repeated States

The Repeated States

Avoiding Repeated States

When we are finding solution by searching in state space tree, some states can be repeatedly explored. This will increase the total cost. Hence we need to avoid repeated states.

In some problems we need to explore all the repeated states again as they may reach to goal state.

For example

Problems where the actions are reversible, such as route-finding problems and sliding-blocks puzzles.

Search tree for these problems are infinite. But if we cut off some repeated states. We can generate only the portion of the tree that engross the state space graph.

In some problems repeated states are not required to explore again as these states will not surely lead to goal states.

In a state space graph we can drop multiple paths and can construct a tree where there is only one path to each state.

For example -

Consider the 8-queen problem. Here each state can be reached through only 1 path. If we formulate the 8-queens problem such that a queen can be placed in any column, then each state with 'n' queens can be reached by n! different paths.

Serious Problems Caused due to Repeated States

1) Because of repeated states solvable problem can become unsolvable if the algorithm is unable to detect repeated states.

2) Because of repeated states looping paths can be generated which can lead to infinite search which is not practical approach.

3) Because of repeated states memory is unnecessarily wasted as same state is maintained multiple times.

Example of State Space that Generate an Exponentially Larger Search Tree

a) Fig 3.6.1 shows a state space in which there are two possible actions leading from A to B, two from B to C and so on. The state space contains d+1 states, where d is maximum depth.

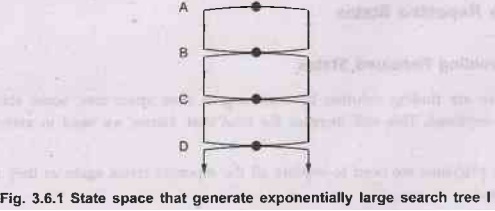
Fig. 3.6.1 State space that generate exponentially large search tree 1

b) In the above search tree, (Fig. 3.6.2) there are 2^d branches corresponding to the 2^d paths through the space.

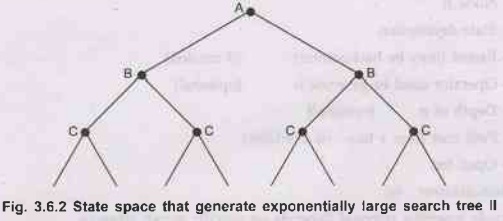
In the search tree shown in Fig. 3.6.3, A is a root node. On a grid each state has four successors, therefore the tree including repeated states has 4^d leaves. But as we can see, only about 2 d² are distinct states within d steps of any given state.

Note If limit of depth in state space tree is specified then it is easy to reduce repeated states which leads to exponential reduction in search cost.

Algorithm that can Avoid Repeated States (Algorithms that forget their history are sure to repeate the states.)

If an algorithm remembers every state that it has visited, then it can be viewed as exploring state space graph directly.

We can device a new algorithm called as graph-search algorithm which is more efficient than earlier tree-search algorithm. A graph-search algorithm maintains two data structures closed list and open list to avoid exporation of those node which are already explored (i.e. trying to avoid repeated states).

Close list: A closed list is a data structure maintained by algorithm which stores every expanded node. Algorithm discards the current node if it matches with node on the closed list.

Open list: A open list is a data structure maintained by algorithm which stores fringe of unexpanded node.

Graph-Search Algorithm

[Data structure required]:

- Node n

-State description

- Parent (may be backpointer)     (if needed)   

-Operator used to generate n      (optional)

- Depth of n(optional)

- Path cost from s to n (if available)

- Open list

• initialization: {s}

• node insertion removal depends on specific search strategy

- Closed list

• initialization: { }

• organized by backpointers to construct a solution path

[Algorithm]:

open : ={s};

closed : = {};

repeat

{

n : = select (open); /* select one node from open for expansion */

if n is a goal

then exit with success; /* delayed goal testing */

expand (n)

/* generate all children of n put these newly generated nodes in open (check duplicates)

put n in closed (check duplicates) */

until open = {};

}

exit with failure

For the above algorithm worst case time and space requirements are proportional to the size of the state space. This may be much smaller than O (b^d).