Solving Linear Recurrence Relations

Solving Linear Recurrence Relations

Definition: Linear Recurrence Relation with constant coefficient.

A linear recurrence relation with constant coefficient is of the form

C₀ a_n + C₁ a_n−1 + C₂ a_{n- 2} + ... + C_k a_n-k, = f(n)

where C is are constants.

A linear homogeneous recurrence relation with constant coefficients of degree K is of the form

a_n = C₁ a_n-1 + C₂ a_n-2 + C_k a_n-k ,where C₁, C₂, …. C_k are real numbers, and C_k ≠ 0.

The three methods of solving recurrence relations are

1. Iteration, 2. Characteristic roots and 3. Generating functions.

Theorem :

Let c₁ and c₂ be real numbers. Suppose that r - c₁ r - c₂ = 0 has two distinct roots r₁ and r₂. Then the sequence {a_n} is a solution of the recurrence relation a_n = c₁ a_n-1 + c₂ a_n-2 if and only if a_n = α₁r₁ⁿ + α₂r₂ⁿ for n = 0, 1, 2, ….. where α₁ and α₂ are constants.

Case (i): If a_n = α₁r₁ⁿ + α₂r₂ⁿ , then the sequence {a_n} is a solution of the recurrence relation.

Given: r₁ and r₂ are roots of

r² - c₁r - c₂ = 0 ….(1)

⇒ r₁² - c₁r - c₂ = 0 ….(2)

⇒ r₂² - c₁r₂ - c₂ = 0 ….(3)

This shows that the sequence {a_n} with a_n = α₁r₁ⁿ + α₂r₂ⁿ is a solution of the recurrence relation.

Case (ii): If the sequence {a_n} is a solution, then a_n = α₁r₁ⁿ + α₂r₂ⁿ for some constants α₁ and α₂.

To show that every solution {a_n} of the recurrence relation a_n = c₁ a_n-1 + c₂ a_n-2 has a_n = α₁r₁ⁿ + α₂r₂ⁿ for n = 0, 1, 2, .... for some constants α₁ and α₂.

Suppose that {a_n} is a solution of the recurrence relation, and the initial conditions a₀ = C₀ and a₁ = C₁ hold.

We will see that there are constants, α₁ and α₂ such that the sequence {a_n} with a_n = α₁r₁ⁿ + α₂r₂ⁿ satisfies these same initial conditons.

This requires that

a₀ = C₀ = α₁ + α₂ ….(1)

a₁ = C₁ = α₁ + α₂ ….(2)

To solve these two equations for α₁ and α₂

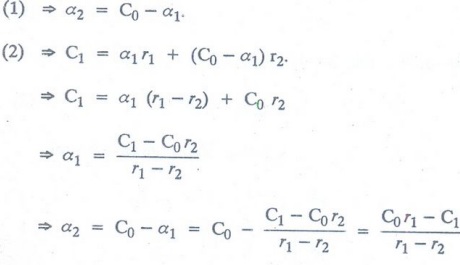
where these expressions for α₁ and α₂ depend on the fact that r₁ ≠ r₂. If r₁ = r₂ then this theorem is not true. Hence, the values of  α₁ and α₂, the sequence {an} with α₁r₁ⁿ + α₂r₂ⁿ satisfies the two initial conditions.

We know that {a_n} and { α₁r₁ⁿ + α₂r₂ⁿ } are both solutions of the recurrence relation a_n = c₁ a_n-1 + c₂ a_n-2 and both satisfy the initial conditions when n = 0 and n = 1.

Since there is a unique solution of a linear homogeneous recurrence relation of degree two with two initial conditions, it follows that the two solutions are the same, (i.e.,) a_n = α₁r₁ⁿ + α₂r₂ⁿ for all non negative integers n.

We have completed the proof by showing that a solution of the linear homogeneous recurrence relation with constant coefficients of degree two must be of the form a_n = α₁r₁ⁿ + α₂r₂ⁿ, where α₁ and α₂ are constants.

Example 1: Find an explicit formula for the Fibonacci numbers.

Solution: The sequence of Fibonacci numbers satisfies the recurrence relation

Example 2: What is the solution of recurrence relation ?

a_n = 5a_n-1 - 6a_n-2 for n ≥ 2, a₀ =1, a₁ = 0.

Solution: Given: a_n = 5a_n-1 - 6a_n-2 ….(1)

Let a_n = rⁿ be a solution of the given equation.

Example 3: What is the solution of the recurrence relation

a_n = 2a_n-1 for n ≥ 1, a₀ = 3.

Solution: Given: a_n = 2a_n-1

(i.e.,) a_n - 2a_n-1 = 0   …. (1)

Let a_n = rⁿ be a solution of (1)

(1) ⇒ rⁿ - 2r^n-1 = 0

⇒ rⁿ [1- 2/r] = 0

⇒ rⁿ [r-2/ r] = 0

The characteristic equation is r - 2 = 0

r = 2

By theorem a_n = α 2ⁿ … (2)

Given a₀ = 3 ⇒ a₀ = α 2⁰ = 3

 ⇒ α = 3

(2) ⇒ a_n = 3 (2ⁿ)

Theorem: Let c₁ and c₂ be real numbers with c₂ ≠ 0. Suppose that r² - c₁r - c₂ = 0 has only one root r₀. A sequence {a_n} is a solution of the recurrence relation a_n = c₁ a_n-1 + c₂ a_n-2 if and only if a_n = α₁r₀ⁿ + α₂r₀ⁿ , for n = 0, 1, 2, … where α₁ and α₂ are constants.

Example 4: What is the solution of the recurrence relation a_n = 8a_n-1 - 16a_n-2 with initial conditions a₂ = 16, a₃ = 80.

Solution : Given: a_n - 8a_n-1 + 16a_n-2 = 0 ….(1)

Let a_n = rⁿ be a solution of (1)

(1) ⇒ r_n – 8r^n-1 + 16r^n-2 = 0

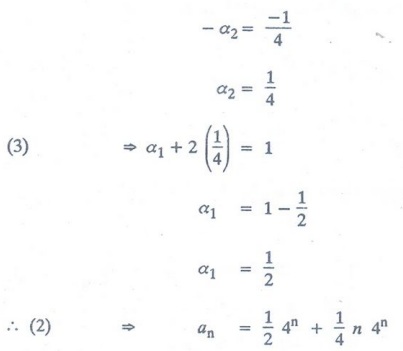
Theorem: Let c₁, c₂, ….. c_k be real numbers. Suppose that the characteristic equation

r^k - c₁r^k-1 - … - c_k = 0

has k distinct roots r₁, r₂, …. r_k. Then a sequence {a_n} is a solution of the recurrence relation

a_n = c₁ a_n-1 + c₂ a_n-2 + ….+ c_k a_n-k

if and only if

a_n = α₁r₁ⁿ + α₂r₂ⁿ +….+ α_kr_kⁿ

for n = 0, 1, 2, …. where α₁, α₂ …. α_k are constants.

Example 5: Find the solution to a_n = 2a_n-1 + 5a_n-2 - 6a_n-3 with a₀ = 7, 4a₁ = -4, a₂ = 8.

Solution: Given: a_n - 2a_n-1 - 5a_n-2 + 6a_n-3 = 0 ... (1)

Let a_n = rⁿ be a solution of (1)

Theorem: Let c₁, c₂, … c_k be real numbers. Suppose that the characteristic equation r^k – c₁r^k-1 - … - c_k = 0 has t distinct roots r₁, r₂, … r_t with multiplicities m₁, m₂,… m_t respectively, so that m_i ≥ 1 for i = 1, 2, ... t and m₁ + m₂ + ... + m_t = k.

Then a sequence {a_n} is a solution of the recurrence relation

a_n = c₁ a_n-1 + c₂ a_n-2 + ….+ c_k a_n-k

if and only if a_n = (α_1,0 + α_1,1 n +….+ α_1,m1-1  n^m1-1 ) r₁ⁿ + (α_2,0 – α_2,1 n +….+ α_2,m2-1  n^m2-1 ) r₂ⁿ + …..+ (α_t,0 + α_t,1 n +….+ α_t,m-1  n^mt-1 ) r₁ⁿ

for n = 0, 1, 2, …. where a_ij are constants for 1 ≤ i ≤ t and 0 ≤ j ≤ m_i -1

Example 6 Find the solution to the recurrence relation a_n = -3a_n-1 -3 a_n-2 - a_n-3 with initial conditions a₀ = 1, a₁ = -2 and a₂ = -1.

Solution : Given: a_n+3 3a_n-1 + 3 a_n-2 + a_n-3 = 0 .... (1)

Let a_n = rⁿ be a solution of (1)

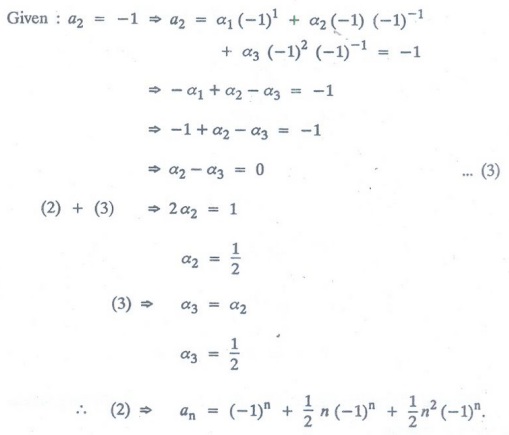
Theorem: If {a_n^(p)} is a particular solution of the non-homogeneous linear recurrence relation with constant coefficients.

a_n = c₁ a_n-1 + c₂ a_n-2 + ….+ c_k a_n-k + F(n)

then every solution is of the form {a_n^(P) + a_n^(h)}, where {a_n^(h)} is a solution of the associated homogeneous recurrence relation.

a_n = c₁ a_n-1 + c₂ a_n-2 + ….+ c_k a_n-k

Example 7: Find all solutions of the recurrence relation a_n = 5a_n-1 - 6a_n-2 + 9ⁿ

Solution: Given: a_n - 5a_n-1 + 6a_n-2 = 9ⁿ ….(1)

Let a_n = c 9ⁿ is a solution of (1)

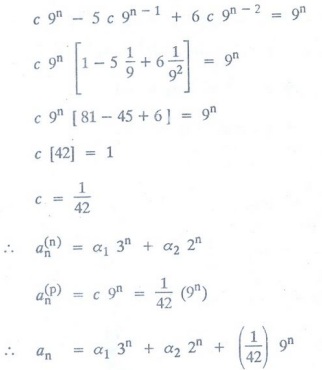
Theorem: Suppose that {a_n} satisfies the linear non-homogeneous recurrence relation

a_n = c₁ a_n-1 + c₂ a_n-2 + ….+ c_k a_n-k + F(n)

where c₁, c₂, ….. c_k are real numbers, and

F (n) = (b_tn^t + b_t-1 n^t-1 + … + b₁n + b₀)sⁿ.

where b₀, b₁, … b_t and s are real numbers. When s is not a root of the characteristic equation of the associated linear homogeneous recurrence relation, there is a particular solution of the form

(p_tn^t + p_t-1 n^t-1 + … + p₁n + p₀)sⁿ.

When s is a root of this characteristic equation and its multiplicity is m, there is a particular solution of the form

n^m(b_tn^t + b_t-1 n^t-1 + … + b₁n + b₀)sⁿ.

Example 8: What form does a particular solution of the linear non homogeneous recurrence relation a_n = 6a_n-1 - 9a_n-2 + F(n) have when F(n) = 3ⁿ, F (n) = n 3ⁿ, F (n) = n² 2ⁿ, and F (n) = (n² + 1) 3ⁿ ?

Solution: The associated linear homogeneous recurrence relation is

a_n = 6a_n-1 - 9a_n-2

Its characteristic equation is r² - 6r + 9 = (r− 3)² = 0.

r = 3, 3

F (n) is of the form p (n) sⁿ

s = 3 is a root with multiplicity m = 2

but s = 2 is not a root

by theorem, particular solution has the form

P₀ n² 3ⁿ if F(n) = 3ⁿ

n² (p₁ n + p₀) 3ⁿ if F(n) = n 3ⁿ

(p₂n² + p₁n + P₀) 2ⁿ if F(n) = n² 2ⁿ

n² (p₂n² + P₁n+P₀) 3ⁿ if F(n) = (n² + 1) 3ⁿ

EXERCISE 2.7

1. Determine which of these are linear homogeneous recurrence relations with constant coefficients. Also, find the degree of those that are.

(a) a_n = 3a_n-1 + 4a_n-2 + 5a_n-3

(b) a_n = a_n-1 + a_{n- 4}

(c) a_n = a_n² - 1 + a_n-2

2. Solve these recurrence relations together with the initial conditions given.

(a) a_n = a_n-1 for n ≥ 1, a₀ = 2

(b) a_n = 4a_n-1 -4a_n-2 for n ≥ 2, a₀ = 6, a₁ = 8

(c) a_n = -4a_n-1 -4a_{n -2} for n ≥ 2, a₀ = 0, a₁ = 1

(d) a_n = 4a_n-2 for n ≥ 2, a₀ = 0, a₁ = 4

3. Find the solution to a_n = 7a_n-2 + 6a_n-3 with a₀ = 9, a₁= 10, and a₂ = 32.

4. Solve the recurrence relation a_n = -3a_n-1 - 3a_n-2 - a_n-3  with a₀ = 5, a₁ = -9 and a₂ = 15.

5. Consider the non-homogeneous linear recurrence relation a_n = 3a_n-1 +2ⁿ.

(a) Show that a_n = -2ⁿ⁺¹ is a solution of this recurrence relation.

(b) Find the solution with a₀ = 1.

6. Find all solutions of the recurrence relation

a_n = 5a_n-1 - 6a_n-2 + 2ⁿ + 3n.

7. Find all solutions of the recurrence relation

a_n = 4a_n-1 - 4a_n-2 + (n + 1) 2ⁿ.

8. Find the solution of the recurrence relation

a_n = 4a_n-1 - 3a_n-2 + 2ⁿ + n + 3 with a₀ = 1 and a₁= 4.

ANSWERS 2.7

1. (a) 3, (b) 4, (c) 2.

2. (a) a_n = 2, (b) a_n = 6 2ⁿ - 2n 2ⁿ, (c) a_n = n(-2)^n-1, (d) a_n = 2ⁿ - (-2)ⁿ

3. a_n = 8(-1)ⁿ - 3(-2)ⁿ + 4 3ⁿ

4. a_n = (n² + 3n+5) (-1)ⁿ

5. (a) 3a_n-1 + 2ⁿ = 3(-2)ⁿ + 2ⁿ(-3+1) = -2ⁿ⁺¹ = a_n,

(b) a_n = 3ⁿ⁺¹ - 2ⁿ⁺¹

6. aⁿ = α 2ⁿ + β 3ⁿ – n 2ⁿ⁺¹ + 3n/2 + 21/4

7. a_n = (α + βn + n² + n³/6) 2ⁿ

8. a_n = -4 2ⁿ –n²/4 – 5n/2 + 1/8 + (39/8) 3ⁿ