Serializability

Serializability

• When multiple transactions run concurrently, then it may lead to inconsistency of data (i.e. change in the resultant value of data from different transaction).

• Serializability is a concept that helps to identify which non serial schedule and find the transaction equivalent to serial schedule.

• For example:

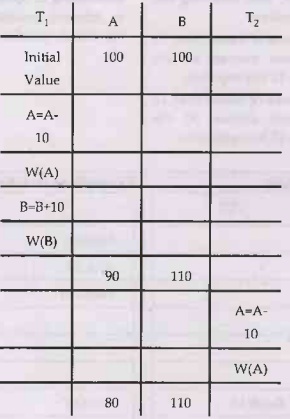
• In above transaction initially T₁ will read the values from database as A= 100, B= 100 and modify the values of A and B, transaction T₂ will read the modified value i.e. 90 and will modify it to 80 and perform write operation. Thus at the end of transaction T₁ value of A will be 90 but at end of transaction T₂ value of A will be  80. Thus conflicts or inconsistency occurs here. This sequence can be converted to a sequence which may give us consistent result. This process is called serializability.

Difference between Serial schedule and Serializable schedule

• There are two types of serializabilities: conflict serializability and view serializability

Conflict Serializability

• Definition: Suppose T₁ and T₂ are two transactions and I₁ and I₂ are the instructions in T₁ and T₂ respectively. Then these two transactions are said to be conflict Serializable, if both the instruction access the data item d, and at least one of the instruction is write operation.

• What is conflict?: In the definition three conditions are specified for a conflict in conflict serializability -

1) There should be different transactions

2) The operations must be performed on same data items

3) One of the operation must be the Write(W) operation

• We can test a given schedule for conflict serializability by constructing a precedence graph for the schedule, and by searching for absence of cycles in the graph.

• Predence graph is a directed graph, consisting of G=(V,E) where V is set of vertices and E is set of edges. The set of vertices consists of all the transactions participating in the schedule. The set of edges consists of all edges Ti→Tj for which one of three conditions holds :

1. Ti executes write(Q) before Tj executes read(Q).

2. Ti executes read(Q) before Tj executes write(Q).

3. Ti executes write(Q) before Tj executes write(Q).     

• A serializability order of the transactions can be obtained by finding a linear order consistent with the partial order of the precedence graph. This process is called topological sorting.

Testing for serializability                                           

Following method is used for testing the serializability: To test the conflictserializability we can draw a graph G = (V,E) where V = vertices which represent the number of transactions. E = edges for conflicting pairs.

Step 1: Create a node for each transaction.

Step 2: Find the conflicting pairs(RW, WR, WW) on the same variable(or data item) by different transactions.

Step 3: Draw edge for the given schedule. Consider following cases

1. Ti executes write(Q) before Tj executes read(Q), then draw edge from T_i to T_j.

2. Ti executes read(Q) before Tj executes write(Q), then draw edge from T_i to T_j

3. Ti executes write(Q) before Tj executes write(Q),, then draw edge from T_i to T_j

Step 4: Now, if precedence graph is cyclic then it is a non conflict serializable schedule and if the precedence graph is acyclic then it is conflict serializable schedule.

Example 3.5.1 Consider the following two transactions and schedule (time goes from top to bottom). Is this schedule conflict-serializable? Explain why or why not.

Solution :

Step 1: To check whether the schedule is conflict serializable or not we will check from top to bottom. Thus we will start reading from top to bottom as

T₁: R(A) -> T₁:W(A) ->T₂:R(A) -> T₂:R(B) ->T₁:R(B)->T₁:W(B)

Step 2: We will find conflicting operations. Two operations are called as conflicting operations if all the following conditions hold true for them-

i) Both the operations belong to different transactions.

ii) Both the operations are on same data item.

iii) At least one of the two operations is a write operation

From above given example in the top to bottom scanning we find the conflict as T₁:W(A)->T₂:R(A).

i) Here note that there are two different transactions T₁ and T₂,

ii) Both work on same data item i.e. A and

iii) One of the operation is write operation.

Step 3: We will build a precedence graph by drawing one node from each transaction. In above given scenario as there are two transactions, there will be two nodes namely T₁ and T₂

Step 4: Draw the edge between conflicting transactions. For example in above given scenario, the conflict occurs while moving from T₁:W(A) to T₂:R(A). Hence edge must be from T₁ to T₂.

Step 5: Repeat the step 4 while reading from top to bottom. Finally the precedence graph will be as follows

Step 6: Check if any cycle exists in the graph. Cycle is a path using which we can start from one node and reach to the same node. If the is cycle found then schedule is not conflict serializable. In the step 5 we get a graph with cycle, that means given schedule is not conflict serializable.

Example 3.5.2 Check whether following schedule is conflict serializable or not. If it is not conflict serializable then find the serializability order.

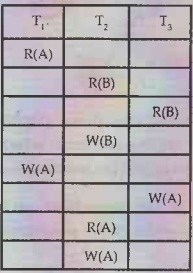
Solution:

Step 1: We will read from top to bottom, and build a precedence graph for conflicting entries. We will build a precedence graph by drawing one node from each transaction. In above given scenario as there are three transactions, there will be two nodes namely T1 T2, and T3

Step 2: The conflicts are found as follows –

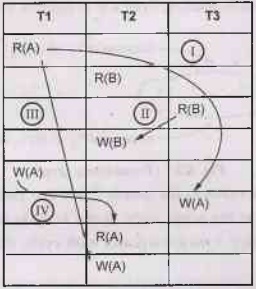
Step 3: The precedence graph will be as follows –

Step 4: As there is no cycle in the precedence graph, the given sequence is conflict serializable. Hence we can convert this non serial schedule to serial schedule. For that purpose we will follow these steps to find the serializable order.

Step 5: A serializability order of the transactions can be obtained by finding a linear order consistent with the partial order of the precedence graph. This process is called topological sorting.

Step 6: Find the vertex which has no incoming edge which is T1. If we delete T1 node then T3 is a node that has no incoming edge. If we delete T3, then T2 is a node that has no incoming edge.

Thus the nodes can be deleted in a order T1, T3 and T2. Hence the order will be T1-T3-T2

Example 3.5.3 Check whether the below schedule is conflict serializable or not.{B2,r2(X),b1,r1(X),W1(X),r1(Y),W1(Y),W2(X),e1,C1,e2,C2}

Solution: b2 and b1 represents begin transaction 2 and begin transaction 1. Similarly, el and e2 represents end transaction 1 and end transaction 2.

We will rewrite the schedule as follows-

Step 1: We will find conflicting operations. Two operations are called as conflicting operations if all the following conditions hold true for them -

i) Both the operations belong to different transactions.

ii) Both the operations are on same data item.

iii) At least one of the two operations is a write operation.

The conflicting entries are as follows –

Step 2: Now we build a precedence graph for conflicting entries.

As there are two transactions only two nodes are present in the graph.

Step 3: We get a graph with cycle, that means given schedule is not conflict serializable.

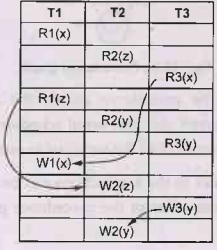
Example 3.5.4 Consider the three transactions T1, T2, and T3 and schedules S1 and S2 given below. Determine whether each schedule is serializable or not? If a schedule is serializable write down the equivalent serial schedule(S).

T1: R1(x) R1(z);W1(x);

T2: R2(x);R2(y);W2(z);W2(y)

T3:R3(x);R3(y);W3(y);

S1: R1(x);R2(z);R1(z); R3(x);R3(y);W1(x);W3(y);R2(y); W2(z);W2(y);

S2: R1(x);R2(z);R3(x);R1(z);R2(y);R3(y);W1(x);W2(z);W3(y);W2(y);

Solution:

Step 1: We will represent the schedule S1 as follows

Step (a): We will find conflicting operations. Two operations are called as conflicting operations if all the following conditions hold true for them -

i) Both the operations belong to different transactions.

ii) Both the operations are on same data item.

iii) At least one of the two operations is a write operation

The conflicting entries are as follows -

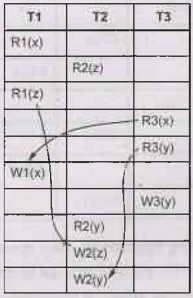
Step (b): Now we will draw precedence graph as follows-

As there is no cycle in the precedence graph, the given sequence is conflict serializable. Hence we can convert this non serial schedule to serial schedule. For that purpose we will follow these steps to find the serializable order.

Step (c): A serializability order of the transactions can be obtained by finding a linear order consistent with the partial order of the precedence graph. This process is called topological sorting.

Step (d): Find the vertex which has no incoming edge which is T3. If we delete T3, then T1 is the edge that has no incoming edge. Finally find the vertex having no outgoing edge which is T2. Hence the order will be T3-T1-T2.

Step 2: We will represent the schedule S2 as follows -

Step (a): We will find conflicting operations. Two operations are called as conflicting operations if all the following conditions hold true for them -

i) Both the operations belong to different transactions.

ii) Both the operations are on same data item.

iii) At least one of the two operations is a write operation

The conflicting entries are as follows -

Step (b): Now we will draw precedence graph as follows-

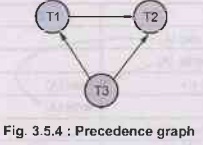
As there is no cycle in the precedence graph, the given sequence is conflict serializable. Hence we can convert this non serial schedule to serial schedule. For that purpose we will follow these steps to find the serializable order.

Step (c): A serializability order of the transactions can be obtained by finding a linear order consistent with the partial order of the precedence graph. This process is called topological sorting.

Step (d): Find the vertex which has no incoming edge which is T3. Finally find the vertex having no outgoing edge which is T2. So in between them is T1. Hence the order will be T3-T1-T2

Example 3.5.5 Explain the concept of conflict serializability. Decide whether following schedule is conflict serializable or not. Justify your answer.

Solution:

Step 1: We will read from top to bottom, and build a precedence graph for conflicting entries.

The conflicting entries are as follows-

Step 2: Now we will build precedence graph as follows

Step 3: There is no cycle in the precedence graph. That means this schedule is conflict serializable. Hence we can convert this non serial schedule to serial schedule. For that purpose we will follow the following steps to find the serializable order.

1) Find the vertex which has no incoming edge which is T1.

2) Then find the vertex having no outgoing edge which is T2. In between them there is no other transaction.

3) Hence the order will be T1-T2.

View Serializability

• If a given schedule is found to be view equivalent to some serial schedule, then it is called as a view serializable schedule.

• View Equivalent Schedule: Consider two schedules S₁ and S₂ consisting of transactions T₁ and T₂ respectively, then schedules S₁ and S₂ are said to be view equivalent schedule if it satisfies following three conditions:

• If transaction T₁ reads a data item A from the database initially in schedule S₁, then in schedule S₂ also, T₁ must perform the initial read of the data item X from the database. This is same for all the data items. In other words –the initial reads must be same for all data items.

• If data item A has been updated at last by transaction T₁ in schedule S₁, then in schedule S₂ also, the data item A must be updated at last by transaction T₁.

• If transaction T₁ reads a data item that has been updated by the transaction T₁ in schedule S₁ then in schedule S₂ also, transaction T₁ must read the same data item that has been updated by transaction T₁. In other words the Write-Read sequence must be same.

Steps to check whether the given schedule is view serializable or not

Step 1: If the schedule is conflict serializable then it is surely view serializable because conflict serializability is a restricted form of view serializability.

Step 2: If it is not conflict serializable schedule then check whether there exist any blind write operation. The blind write operation is a write operation without reading a value. If there does not exist any blind write then that means the given schedule is not view serializable. In other words if a blind write exists then that means schedule may or may not be view conflict.

Step 3: Find the view equivalence schedule

Example 3.5.6 Consider the following schedules for checking if these are view serializable or not.

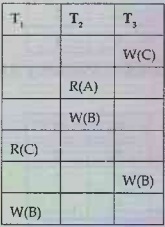
Solution:

i) The initial read operation is performed by T₂ on data item A or by T₁ on data item C. Hence we will begin with T₂ or T₁. We will choose T₂  at the beginning.

ii) The final write is performed by T₁ on the same data item B. Hence T₁ will be at the last position.

iii) The data item C is written by T₃ and then it is read by T₁. Hence T₃ should before T₁.

Thus we get the order of schedule of view serializability as T₂ - T₁ – T₃

Example 3.5.7 Consider following two transactions:

T₁: read(A)

read(B)

if A=0 then B:=B+1;

write(B)

T₂: read(B);

read(A);

if B=0 then A:=A+1;

write(A)

Let consistency requirement be A=0 V B=0 with A=B=0 the initial values.

1) Show that every serial execution involving these two transactions preserves the consistency of the Database?

2) Show a concurrent execution of T₁ and T₂ that produces a non serializable

schedule?

3) Is there a concurrent execution of T₁ and T₂ that produces a serializable

schedule?

Solution: 1) There are two possible executions: T₁ ->T₂ or T₂->T₁

Consider case T₁->T₂ then

AvB =A OR B=FVT-T. This means consistency is met.

Consider case T₂->T₁ then

AvB = A OR B = FvT=T. This means consistency is met.

2) The concurrent execution means interleaving of transactions T₁ and T₂. It can be

This is a non-serializable schedule.

(3) There is no concurrent execution resulting in a serializable schedule.

Example 3.5.8 Test serializability of the following schedule:

i) r1(x);r,(x);w,(x);r2(x);w ̧(x) ii) 1,(x);12(x);W;(x);1,(x);w,(x)

Solution:

i) r₁(x);r₃(x);w₁(x);r₂(x);w₃(x)

The r₁ represents the read operation of transaction T₁, w₃ represents the write operation on transaction T₃ and so on. Hence from given sequence the schedule for three transactions can be represented as follows:

Step 1: We will use the precedence graph method to check the serializability. As there are three transactions, three nodes are created for each transaction.

Step 2: We will read from top to bottom. Initially we read r,(x) and keep on moving bottom in search of write operation. Here all the transactions work on same data item i.e. x. Now we get a write operation in T₁ as w₃(x). Hence the dependency is from T₁ to T₃. Therefore we draw edge from T₁ to T₃.

Similarly, for r₃(x) we get w₁(x) pair. Hence there will be edge from T₃ to T₁. Continuing in this fashion we get the precedence graph as

Step 3: As cycle exists in the above precedence graph, we conclude that it is not

serializable.

ii) r₃(x);r₂(x);w₃(x);r₁(x);w₁(x)

From the given sequence the schedule can be represented as follows:

Step 1: Read the schedule from top to bottom for pair of operations. For r₃(x) we get w₁(x) pair. Hence edge exists from T, to T, in precedence graph.

There is a pair from r₂(x): w₃(x). Hence edge exists from T₂ to T₃.

There is a pair from r₂(x): w₁(x). Hence edge exists from T₂ to T₁.

There is a pair from w₂(x): r₁(x). Hence edge exists from T₃ to T₁.

Step 2: The precedence graph will then be as follows-

Step 3: As there is no cycle in the above graph, the given schedule is serializable. 

Step 4: The searializability order for consistent schedule will be obtained by applying topological sorting on above drawn precedence graph. This can be achieved as follows,

Sub-Step 1: Find the node having no incoming edge. We obtain T₂ is such a node. Hence T₂ is at the beginning of the serializability sequence. Now delete T₂. The Graph will be

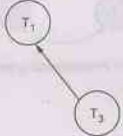
Sub-Step 2: Repeat sub-Step 1, We obtain T₃ and T₁ nodes as a sequence.

Thus we obtain the sequence of transactions as T₂, T₃ and T₁. Hence the serializability order is

r₂(x);r₃(x);w₃(x):r₁(x);w₁(x)

Example 3.5.9 Consider the following schedules. The actions are listed in the order they are scheduled, and prefixed with the transaction name.

S1: T1: R(X), T2: R(X), T1: W(Y), T2: W(Y)TI: R(Y), T2: R(Y)

S2: T3: W(X), TI: R(X), T1: W(Y), T2: R(Z),T2: W(Z) T3: R(Z)

For each of the schedules, answer the following questions:

i) What is the precedence graph for the schedule?

ii) Is the schedule conflict-serializable ? If so, what are all the conflict equivalent serial schedules?

iii) Is the schedule view-serializable? If so, what are all the view equivalent serial schedules ? AU: May-15, Marks 2 +7 +7

Solution: i) We will find conflicting operations. Two operations are called as conflicting operations if all the following conditions hold true for them -

• Both the operations belong to different transactions.

• Both the operations are on same data item.

• At least one of the two operations is a write operation

For S1: From above given example in the top to bottom scanning we find the conflict as

   • T1: W(Y), T2: W(Y) and

    • T2: W(Y), T1: R(Y)

Hence we will build the precedence graph. Draw the edge between conflicting transactions. For example in above given scenario, the conflict occurs while moving from T₁:W(Y) to T₂:W(Y). Hence edge must be from T₁ to T₂. Similarly for second conflict, there will be the edge from T₂ to T₁

For S2: The conflicts are

   • T3: W(X), T1: R(X)

   • T2: W(Z) T3: R(Z)

Hence the precedence graph is as follows –

i)

   • S1 is not conflict-serializable since the dependency graph has a cycle.

   • S2 is conflict-serializable as the dependency graph is acylic. The order T2-T3-T1 is the only equivalent serial order

ii)

   • S1 is not view serializable.

   • S2 is trivially view-serializable as it is conflict serializable. The only serial order allowed is

T2-T3-T1.

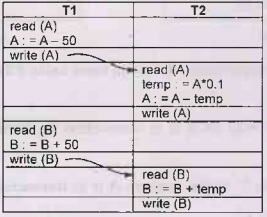
Example 3.5.10 Check whether following schedule is view serializable or not. Justify your answer. (Note: T1 and T2 are transactions). Also explain the concept of view equivalent schedules and conflict equivalent schedule considering the example schedule given below :

Solution:

Step 1: We will first find if the given schedule is conflict serializable or not. For that purpose, we will find the conflicting operations. These are as shown below –

The precedence graph is as follows -

As there exists no cycle, the schedule is conflict serializable. The possible serializability order can be T1 - T2

Now we check it for view serializability. As we get the serializability order as T1 - T2, we will find the view equivalence with the given schedule as serializable schedule.

Let S be the given schedule as given in the problem statement. Let the serializable schedule is S'={T1,T2}. These two schedules are represented as follows:

Now we will check the equivalence between them using following conditions -

(1) Initial Read

In schedule S initial read on A is in transaction T1. Similarly initial read on B is in transaction T1.

Similarly in schedule S', initial read on A is in transaction T1. Similarly initial read on B is in transaction T1.

(2) Final Write

In schedule S final write on A is in transaction T2. Similarly final write on B is in transaction T2.

In schedule S' final write on A is in transaction T2. Similarly final write on B is in transaction T2

(3) Intermediate Read

Consider schedule S for finding intermediate read operation.

Similarly consider schedule S` for finding  intermediate read operation

In both the schedules S and S', the intermediate read operation is performed by T2 only after T1 performs write operation.

Thus all the above three conditions get satisfied. Hence given schedule is view serializable.

Review Questions

1. Explain Conflict serializability and view serializability. AU: May-18, Marks 6, Dec.-15, Marks 8

2. Discuss in detail about the testing of serializability. AU: May-19, Marks 13