Semigroups and Monoids

Semi-group and Monoids

Theorem 1: The composition of semi-group homomorphism is also a semi-group homomorphism.

Proof :

Definition: Semi-group endomorphism :

A homomorphism of a semi-group into itself is called a semi-group endomorphism.

Theorem 2. The set of all semi-group endomorphisms of a semi-group is a semi-group under the operation of left composition.

Proof: Let F be the set of all semi-group homomorphism

f: S →S where (S, *) is a semigroup.

To prove: (F, o) is a semi-group with binary operation o, the left composition of mapping.

Proof :

(i) Closure: ∀ f, g Є F ⇒ f o g Є F

(ii) Associative: ∀ f, g, h Є F, ∀ a Є S

(f o g) o h (a) = f o g (h (a))

= f (g (h (a)))

= f (g o h (a))

= f o (g o h) (a)

⇒ (f o g) = f o (g o h)

(F, o) is a semi-group.

Note: Infact (F, o) is a monoid, because the identity mapping I is the identity under o. Thus (F, o, I) is a monoid. Therefore the set of all semigroup homomorphisms of a semigroup is a monoid.

Theorem 3. Let (S, *) be a given semi-group. There exists a homomorphism g: S→S^S, where (S^S, o) is a semi-group of functions from S to S under the operation of (left) composition.           [A.U N/D 2011]

Proof: For any a Є S

We define a function f_a: S→S,

defined by f_a (b) = a*b, ∀ b Є S

f (a) Є S^S

Now, we define g: S→ S^S by

g (a) = f_a, ∀ a Є S

Let a, b Є S, then a*b Є S

g (a* b) = f_a*b

f_a*b (c) = (a*b) * c, ∀ c Є S

= f_a (b*c)

= f_a (f_b (c))

= f_a o f_b (c)

⇒ f_a*b = f_a o f_b

⇒ g (a*b) =  g(a) o g(b)

Hence, the proof.

Theorem 5. Let (S, *) and (T, ∆) be two semigroups and g be a semigroup homomorphism from (S, *) to (T, ∆). Corresponding to the homomorphism g, there exists a congruence relation R on (S, *) defined by

x R y            iff g (x) = g(y)            for x, y Є S

Proof: It is easy to see that R is an equivalence relation on S. Let x₁, x₂, x₁', x₂' Є S such that x₁ R x₁' and x₂ R x₂'. From

g (x₁*x₂) = g (x₁) ∆ g(x₂) = g(x₁) ∆ g(x₂) = g(x₁' * x₂')

it follows that R is a congruence relation on (S, *).

Property 1: A semigroup homomosphism preserves the property of associativity.

Solution: Let a, b, c Є S

g [(a+b) *c] = g(a*b) o g(c)

= [g (a) o g (b)) o g (c)]   …..(1)

g[a* (b*c)] = g(a) o g(b*c)

= g (a) o g (b) o g (c)] …..(2)

But in S,   (a * b) * c = a * (b * c) ∀ a, b, c Є S

g [(a * b) * c ] = g[a* (b * c)]

⇒ [g (a) o g (b)] o g (c) = g(a) o [g (b) o g (c)]

The property of associativity is preserved.

Property 2: A semigroup homomorphism preserves idempotency.

Solution: Let a Є S be an idempotent element.

a* a = a

g (a*a) = g(a)

g(a) o g (a) = g(a)

This shows that g (a) is an idempotent element in T.

The property of idempotency is preserved under semigroup homomorphism.

Property 3: A semigroup homomosphism preserves commutativity.

Solution: Let a, b Є S.

Assume that a * b = b * a

g (a * b) = g (b * a)

g (a) o g (b) = g(b) o g (a)

This means that the operation o is commutative in T.

The semigroup homomorphism preserves commutativity.

Property 4: Show that every finite semigroup has an idempotent element.

Solution: Consider the subsemigroup S generated by s (i.e.,) S = {s, s₂, s₃, ... sⁿ}, where n is finite. S is a finite subset of a finite semigroup G. Therefore there exist r₁, r₂ such that sr₁ sr₂. Without loss of generality, we assume that r₁ > r₂.

Now we have two cases.

Case 1: Suppose r₁ – 2r₂ ≥0

Put r = r₁ – 2r₂

Now

s^r1 s^r = s^r2 s^r = s^r1-r2

(r₂+r = r₂ + r₁ – 2r₂ = r₁ – r₂)

S^r1+r = s^{2(r1 – r2)}

This implies that S has an idempotent.

Case 2: Suppose r₁ – 2r₂ < 0

Put r₁ - r₂

s^r1 s^r = s^r2+r = s^r1 = s^r2

s^r1 s^r s^r = s^r2+r = s^r1 = s^r2

Proceeding in this way, we can find an integer r1'≥ 22 such that

s^r1 = s^r2

which leads to case 1.

Thus we have proved that S has an idempotent which inturn implies that the semigroup G has an idempotent.

Problems under semi-group and monoid

Example 1. Give an example of a semi-group which is not a monoid.  [A.U. M/J 2009]

Solution: Let D = {..., -4, -2, 0, 2, 4, ...}

 (D,.) is a semi-group but not a monoid since multiplicative identity is 1, but 1Є D

Example 2. Give an example of a monoid which is not a group.

Solution: (Z+,.) is a monoid which is not a group.

Since ∀ a Є G, 1/a € G

Example 3. What do you call a homomorphism of a semi-group into itself? [A.U. A/M 2003]

Solution: A homomorphism of a semi-group into itself is called a semi-group endomorphism.

Example 4. If (Z, +) and (E, +) where Z is the set all integers and E is the set of all even integers, show that the two semi groups (Z, +) and (E, +) are isomorphic.      [A.U. N/D 2010]

Solution :

Step 1: We define the function

G: Z → E given by g (a) = 2a where a Є Z

Step 2: Suppose g (a1) = g (a2) where a₁, a₂ Є Z

Then 2a₁ = 2a₂ i.e., a₁ = a₂

Hence mapping by g is one-to-one.

Step 3: Suppose b is an even integer

Let a = b/2. Then a Є Z and

g (a) = g (b/2) = 2.b/2 = b

i.e., every element b in E has a preimage in Z.

So mapping by g onto.

Step 4: Let a and b EZ

g (a + b) = 2(a + b)

= 2a + 2b

= g (a) + g (b)

Hence, (Z, +) and (E, +) are isomorphic semigroups.

Example 5. If * is a binary operation on the set R of real numbers defined by a + b = a + b + 2ab,

(1) Find <R, *> is a semigroup.

(2) Find the identify element if it exists.

(3) Which elements has inverse and what are they?           [A.U A/M 2011]

Solution :

(1) (a*b) *c = (a + b + 2ab) + c + 2 (a + b + 2 ab) c

= a + b + c + 2 (ab + bc + ca) + 4 abc

a * (b*c) = a + (b + c + 2bc) + 2a (b + c + 2bc)

= a + b + c + 2 (ab + bc + ca) + 4abc

Hence, (a*b) *c = a* (b*c)

i.e., is associative.

(2) If the identity element exists, let it be e.

Then for any a Є R.

a * e = a

i.e., a + e + 2ae = a

i.e., e (1 + 2a) = 0

e = 0, since 1+ 2a ≠ 0, for any a Є R

(3) Let be a^-1 the inverse of an element a Є R. Then a * a^-1 = e

i.e., a + a^-1 + 2a. a^-1 = 0

i.e., a^-1.(1+2a) = -a

a^-1 = -a /1 + 2a

If a ≠ 1/2 then a^-1 = -a /1 + 2a

Example 6. Let < M, *,e_M > be a monoid and a Є M. If a invertible, then show that its inverse is unique.         [A.U A/M 2011]

Solution: Let b and c be elements of M

such that

a*b = b*a = e and

a*c = c*a = e

since

b = b * e

= b * (a*c)

= (b*a) * c

= e*c

= c

Example 7. Show that a semi-group with more than one idempotents cannot be a group. Give an example of a semi-group which is not a group.   [A.U N/D 2014]

Solution: Let (S, *) be semi-group.

Let a, b are two idempotents

a*a = a and b*b = b

Let us assume that (S, *) is group then each element has the inverse.

(a * a) * a^-1 = a * (a * a^-1)

L.H.S = (a * a) * a^-1 = a * a^-1         [ a * a = a]

= e

(a * a) * a ^-1 = e …..(1)

also R.H.S = a * (a * a ^-1) = a * e = a …..(2)

From (1) & (2), we get a = e

Similarly we can prove that b = e

In a group we can not have two identities and hence (S, *) cannot be group.

This contradiction is due to an assumption that (S,*) has two idenpotents.

Example: Let S = {a, b, c) under the operation *

(S, *) is a semi-group which is not a group.

Example 8: Let (N,+) be the semigroup of natural numbers and (S, *) be the semigroup of on S = {e, 0, 1} with the operation * given by

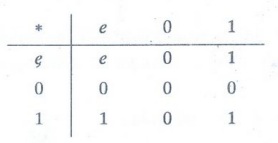
A mapping g: N→S given by g (0) = 1 and g (j) = 0 for j ≠ 0. Is g is a semigroup homomorphism.

Solution: Though both (N, +) and (S, *) are monoids with identities 0 and e respectively, g is not a monoid homomorphism because g (0) ≠ e.

g is semigroup homomorphism.

Example 9: Find all semigroup of (Z₆, X₆) where Z₆ = {[0], [1], [2], [3], [4], [5]}

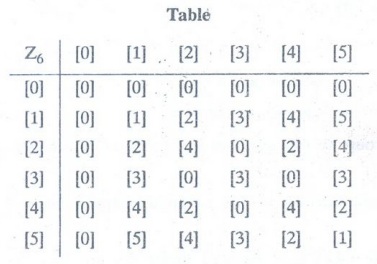
Solution: {[0]}, {[0], [1]}, {[1]}, {[1], [2], [4]}, {[0], [1], [2], [4]}, {[2], [4]}, {[0], [3], [4]}, {[1], [5]}, {[0], [1], [5]}, {[0], [4]}, {[0], [1], [4]}, {[2], [0], [3]}, {[0], [1], [2], [3]}

Example 10: Is it true that a semigroup homomorphism preserves identity? Justify your answer. [OR] Prove by an example that semigroup homomorphism need not preserve an identity.

Solution: Semigroup homomorphism need not preserve an identity.

Let W = {0, 1, 2, ..}. Then (W, +) is a semigroup with identity element 0. Let S = {e, o, 1} and * be the operation on S given by

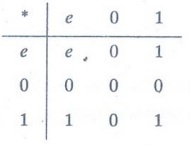
Then, (S, *) is a semigroup with identity e.

Define a mapping g: W→S by

g(0) = 1 and g (i) = 0 for i ≠ 0.

We can see that g (a + b) = g (a) * g (b) for all a, b Є W. Thus g is a semigroup homomorphism. But g (0) = 1 ≠ e. Thus g doesn't preserve the identity.

Example 11 Let S = {a, b}. Show that the semi group (S^s, . ) is not commutative where . is the left composition of functions.

Solution: Let S = {a, b} then (S^s, .) is an algebra of set of functions from S to S with left composition '.’ as an operation. Clearly S^s contain 2² functions (that is 4 functions).

S^s = (f₀, f₁, f₂, f₃), defined by

f₀ (a) = a

f₀ (b) = a

f₁ (a) = a

f₁ (b) = a

f₂ (a) = b

f₂ (b) = b

f₃ (a) = b

f₃ (b) = a

Table is the composition table for (Ss, .) from the table one can see that f₂ o f₁ ≠ f₁ o f₂  and hence (S^s, .) is not commutative.

Example 12:  Let (S, *) be a semigroup and z  Є S be a left zero. Show that for any x Є S, x*z is also a left zero.

Solution: Let (S, *) be a semigroup. Therefore (S, *) is closed under * and * is associative.

Therefore for any x, y, z we have

(x * y) * z = x* (v* z)

As z is left zero x * z = z for all x Є S.

Therefore y * (x*z) = z because y * (x * z) = y * z = z = x*z for all y Є S, which implies that x*z is also a left zero of s.

Example 13 An element a Є S is left cancellable for a semigrop (S, *) if for all x, y Є S, a * x = a * y ⇒ x= y. Show that if a and b are left cancellable then a*b is also left cancellable.

Solution: Let a, b ⇒ S, where (S, *) are left cancellable that

a * x = a * y

⇒ x = y and

b*x =b*y

⇒ x = y

Now we shall show that

(a*b) * x = (a*b) * y

⇒ x = y

As (S, *) is associative

(a*b) * x = a * (b*x) and

(a*b) * y = a* (b*y)

As (a * b) *x = (a* b) *y we have

a* (b*x) = a* (b* y)

using left cancellable property of a.

b*x = b*y ⇒ x = y, because b is left cancellable.

Therefore, (a*b) *x = (a*b) *y

⇒ x= y, which proves the claim.

Example 14: Let A = {0, 1} and A* be the free semigroup generated by A by the operation of concatenation. Show that the relation R defined for x, y Є A* such that x R y iff x and y contain the same number of I_s, is a congruence relation. Suggest a homomorphism which induces R on A*.

Solution: It is easy to see that R is a congruence relation on (A*, o) where o denotes concatenation. Consider the semigroup (N, +) and a mapping g: A* → N such that for any x Є A*, g(x) = n where n is the number of I_s in x.

Naturally, for any x, y Є A*,

g (xy) = g(x) + g (y)

so that g is a homomorphism from (A* o) to (N, +).

Now for x, y Є A*,

g(x) = g(y) ↔ x R y

so that the congruence relation R is induced by the homomorphism g.

Example 15. If is the operation defined on S = Q× Q, the set of ordered pairs of rational numbers and given by (a, b) * (x, y) = (ax, ay + b), show that (S,*) is a semi group. Is it commutative? Also find the identity element of S.   [A.U N/D 2012]

Solution: Given: (a, b) * (x, y) = (ax, ay + b) ….(1)

To prove (S, *) is a semigroup.

i.e., To prove : * operation is associative.

{(a, b) * (x, y)) * (c, d)

= (ax + ay + b) * (c, d)     by (1)

= (acx, adx + ay + b) …. (2)   by (1)

(a, b) * {(x, y) * (c, d)}

= (a, b) * {cx, dx + y}

= (acx, adx + ay + b) …. (3)

From (2) & (3), * is associative on S.

To prove (S, *) is not commutative.

(x, y) * (a, b) = (ax, bx + y) …. (4)

(a, b) * (x, y) = (ax, ay + b) …. (5)

(4) ≠ (5) {S, *} is not commutative.

To find the identity element of (S, *)

Let (e₁, e₂) be the identity element of (S, *), ∀ (a, b) Є S

i.e., (a, b) * (e₁, e₂)

(ae₁, ae₂ + b) = (a, b)

⇒ ae₁ = a, ae₂ + b = b

⇒ e₁ = 1, ae₂ = 0

e₂ = 0

(1, 0) is the identity element of {S, *}

MONOID :

Example 1: Let X be any given set and P (X) is its power set. Then find the zeros of the semigroups (P (X), ∩) and (P (X), U). Are these monoids? If so, what are the identities ?

Solution: Let X be any given set. Then its power set p (X) contains 2^x subsets of X.

If Z Є p (X) is zero with respect to the operation ∩ for p (X), then Z ∩ X₁ = X₁ Ո Z = Z implies that Z = ϕ empty set.

The zero Z of (p (X), U) is such that Z U X₁ = X₁UZ = Z for all X₁ Є p (X), implies that Z = the whole set X.

The identity of (p (X), ∩) is given by the set S_e, such that S∩S_e = S_e∩S = S for all S Є P (X).

Therefore S_e = X, the whole set.

The identity of (p (X), U) is S_e, which satisfies the property that S = S_e US = SUS_e. Therefore S_e is the empty set ϕ.

With this it is clear that (p(X) ∩ X) and (p(X) U ϕ ) are monoids.

Example 2: Let V = {a, b} and A be set of all sequences on V including ˄ beginning with a. Show that (A, o ˄) is a monoid.

Solution: Let V = {a, b} and A be set of all sequence on V including ˄ beginning with a. Then A= {˄, a, ab, aa, ab, aba, abb, ...}. Let o be a concatenation operation on the sequences in A. Clearly for any two elements a, b Є A.

α ο β = a ß also belongs to A and hence (A, o) is closed. Also 'o' is associative. Because

(α o β) ο γ = αβγ = α o (β γ)

= (αοβογ)

˄ is identity as ˄ 。α = α o ˄ = α for all α Є Α.

Therefore (A, o ˄) is a monoid.

Example 3: Show that the set N of natural numbers is a semigroup under the operation x * y = max (x, y). Is it a monoid ?

Solution: Let N = {0, 1, 2, ....}

Define the operation x * y = max {x, y) for x, y Є N.

Clearly (N, *) is closed because x * y max {x, y} Є N and * is associative as

(x * y) *z = max {x * y, z}

= max {max {x, y}, z}

= max {x, y, z}

= max {x, max {y, z}

= max {x, max {y *z}

= x* (y * z)

Therefore, (N, *) is semigroup.

The identity e of (W, *) must satisfy the property that x*e = e*x = e. But as x * e = e * x = max {x, e}, e = x, ∞ (the infinity). Therefore (N, *, ∞) is monoid.

Example 4: Every monoid (M, *, e) is isomorphic to (M^M, o , ∆) where ∆ is the identity mapping to M.

Solution: Define a mapping f from M^M to

f(a) = f_a where fa Є M^M

defined by f_a (b) = a*b for any bЄM

Now

f (a*b) = f_a*b, where

f_a*b (c) = (a + b) * c = a * (b*c)

= f_a (b*c) = f_a f_b (c)

Therefore, f_a*b = f_a o f_b, which implies that

= f(a*b) = f_a*b = f_a°f_b = f (a) o f(b)

Therefore ƒ is a homomorphism.

Clearly f is one-one and onto and hence ƒ is an isomorphism from M onto M^M

Example 5: Prove that monoid homorphism preserves invertibility and monoid epimorphism preserves zero element (if it exists).     [A.U. N/D 2003]

Sol. Let (M, *, C_M) and (T, ∆, e_T) be any two monoids and let g: M→T be a monoid homomorphism. If a Є M is invertible, let a^-1 be the inverse of a in M. We will now show that g (a^-1) will be an inverse of g (a) in T.

a *a^-1 = a ^-1 * a = e_м (By definition of inverse)

So   g(a*a^-1) = g(a^-1*a) = g(e_M)

Hence g (a) ∆ g (a^-1) = g(a^-1) ∆ g(a) = g(e_M)   (since g is a homomorphism)

But

g (e_M) = е_т  (since g is a monoid hmomorphism)

g (a) ∆ g(a^-1) = g(a^-1) ∆ g(a) = e_T

This means g (a^-1) is an inverse of g (a) i.e., g (a) is invertible. Thus the property of invertibility is preserved under monoid homomorphism.

Assume g is monoid epimorphism

t ∆ g (z) = g (b) ∆ g(z) = g(b* z) = g(z)

and 8 (2) Δt = g (z) ∆ g (b) = g(z * b) = g(z)

g(z) is zero element of T.

Example 6: On the set Q of all rational numbers, the operation * is defined by ab = a+b- ab. Show that, under this operation, Q is a commutative monoid.

Solution

Since a + b - ab is rational number for all rational numbers a, b the given operation * is a binary operation on Q.

We note that, for all a, b, c Є Q.

(a*b) *c = (a + b - ab) * c

= (a + b - ab) + c - (a + b - ab) c

= a + b - ab + c – ac - bc + abc

= a + (b + c - bc) -a (b + c - bc).

= a* (b + c - bc)

= a * (b*c)

Hence is associative.

We check that, for any a Є Q,

a*0= a +0 - a.0 = a

and 0 * a = 0 + a - 0.a = a

As such, 0 is the identity element in Q under the given *.

The definition of * itself indicates that * is commutative.

Thus, under the given *, Q is a commutative monoid with 0 as the identity.

Example 7: Let V = {a, b}. Show that (V*, o, A) is an infinite monoid.

Solution: While defining alphapet and set of strings V*, we proved that (V*, o, ˄) is a monoid where ˄ is a empty string. So, it is enough to show that V* is an infinite set. As a is an element of V, a, aa, aaa, aaaa,… b, bb, bbb, bbbb, ... ab, abb, abbb, …..are the elements of V* and hence V* contains infinitely many strings including empty set.

Example 8. Let (M, *) be a monoid. Prove that there exists a subset T≤M^M such that (M, *) is isomorphic to the monoid (T, O); here M^M denotes the set of all mappings from M to M and "O" denotes the composition of mappings. [A.U M/J 2014]

Proof : ∀a ЄM, let g (a) = f_a where f_a Є M^M is defined by

f_a (b) = a *b for any b Є M.

Clearly, g is a function from M to M^M

Now, g (a*b) = f_a*b, where f_a*b(c) = = (a * b) * c

= a * (b*c)     [ Associative law]

= f_a (b*c)

= (f_a o f_b) (c)

f_a*b = f_a o f_b

Hence, g (a*b) = f_a*b

= f_a o f_b

= g(a) o g (b)

g (a*b) = g(a) o g(b) ∀a, b Є M

g: M→M^M is a homomorphism.

Corresponding to an element a Є M, the function f_a is completely determined from the entries in the row corresponding to the element a in the composition table of (M, *).

Since, f_a = g(a), every row of such a table determines the image of 'a' under the homomorphism g.

Let g (M) be the image of M under the homomorphism g such that g (M) ≤ M^M

Let a, b Є M, then g (a) = f_a and g (b) = f_b are elements in g (M).

Also, f_a o f_b = f (a + b) Є g (M) since, a*b Є M.

g (M) is closed under the operation, composition of functions.

The mapping g: M→g (M) is onto size (M, *) is a monoid. No two rows of the composition table can be identical.

⇒ Two functions defined by these rows will be identical.

The mapping g: M→g (M) is one-to-one and onto.

g: M→g (M) is an isomorphism. If e is the identity element of M then we define f_c (a) = a ∀ a ЄM.

Clearly, this function f_e Є T = g (M)

Now,    f_e = g (e)

Also    f_a o f_e = g (a) o g (e)

= g(a*e) = g(a)

f_a o f_e = g (a) = f (a).

This shows that f_e is the identity element of T = g (M), since f_a, f_b ЄT, f_a o f_b ЄT.

T is closed under the operation composition of functions.

T = g (M) is a monoid.

Further, g: M→T is a isomorphism.

Hence, (M, *) is isomorphic to the monoid (T, o).