Searching with Partial Information

Searching with Partial Information

AU: Dec.-10

All the earlier search strategies we have seen, assumed that environment is fully observable and deterministic.

In such a environment agent -

1) Knows what is the effect each action.

2) Can calculate exactly which state results from any sequence of actions.

3) Knows which state it is in.

4) Does not get new information after each action.

If environment is not fully observable and knowledge of the states and actions is incomplete then agent has different types of task environment. Such a environment leads to three distinct types of problems -

1) Sensorless problems             

2) Contigency problems

3) Exploration problems.

Sensorless Problems (Conformant Problems)

In this type of problems -

A) Agent has no sensors at all

B) According its own knowledge agent could be in one of several possible initial states.

C) As agent has several possible initial states each action can lead to one of the several possible successor states.

• Solving sensorless problems in a fully observable, completely known, deterministic environment →

In sensorless problem agent already have predefined knowledge about its various states. Out of these state set only one of the state is going to be initial state. Though agent has no sensor, hence no percepts, still from its own state and action it can reach to certain conclusion states, through which it can further reach to goal state. It means that we can say agent can coerce (force to reach) the world to reach at a perticular expected state on his own.

Steps taken to solve the problem are as follows -

1) First agent searches for belief state instead of physical state.

[The belief state - it is a set of states representing agent's current belief about the possible physical states it might be in. For finding such belief state agent should have reasoning for each state it can be in, based on its original knowlege].

2) Initial state is belief state which can further mapped to another belief state.

3) Action is applied to belief state by taking union of the results obtained from applying the action to each physical state in the belief state.

4) We now get a path which connects several belief states.

5) Solution is a path that leads to a belief state, all of whose members are goal states.

Note If the physical state space has 's' states, the belief state space will have 25 belief states.

For Example

• Black ball picker robot

Contigency Problem

If environment is partially observable or if actions are uncertain, then agent can sense and perceive new information after each action. This new information can lead to new problem (or critical situation) which is called as contigency. If this situation occurs then agent needs to plan next action to handle this contigency.

• Solving contigency problem -

1) For contigency problem one needs to form a tree, here each branch of a tree may be selected depending upon the percepts received upto that point in the tree.

2) Then by searching and expanding previous level agent can reach to a goal.

In some situations for contigency problems we get purely sequential solutions.

Note Searching algorithm for contigency problems are more complex than algorithms we have studied so far.

The agent design is also different for these problems, because agent can act before it has found a guaranteed plan.

Agent continue to solve problem, considering new information and minimizing he contigency by checking the output of its action. This is termed as interleaving of searching and execution. [That is alternately search and execution is done].

For example:

Trading agent

• Special case of contigency problem: A contigency problem is called as adversarial problem if the uncertainty is caused by the actions of another agent. (More adverse situation).

For example -

Agent in game of chess.

Extreme Case of Contigency Problem

Exploration problem: When state as well as the actions of the environment are unknown the agent must act to discover them. The interleaving of searching and execution would be useful to solve exploration problem.

For example -

The boat driving robotic agent.

Solved Examples

Example 3.7.1 Write production rules for eight puzzle problem.

Solution: A block of 8 tiles is given in a certain position. One tile could be moved at the vacant position and the desired goal state is to be achieved.

The state space representation for 8-puzzle problem.

The heuristic used for the solution is:

See if tile is in its right position i.e. at the position of the Goal state. If so then assign weight (tile) = 1. If not then don't assign any weight to it. Now add the weights of all tiles and select the next state as the situation with maximum weight. This is because higher the weight more number of tiles are in their correct positions and we can get the Goal state.

Now here there can be maximum 4 possible moves i.e. move1, move2, move3, move4.

So the production rules are:

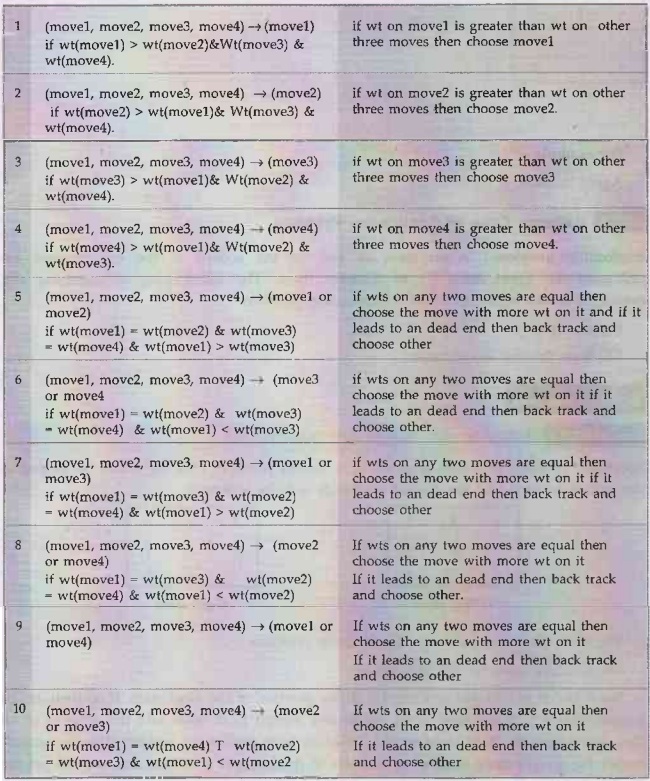
Now lets apply these rules to solve below problem:

Step 1:

So applying rule 2 we choose move2.

Step 2:

So applying rule 5 we chose move2.

Step 3:

So applying rule 1 we choose move1.

Step 4:

So applying rule 1 we choose movel.

Step 5:

So applying rule 2 we choose move 2.

And we get the Goal State.

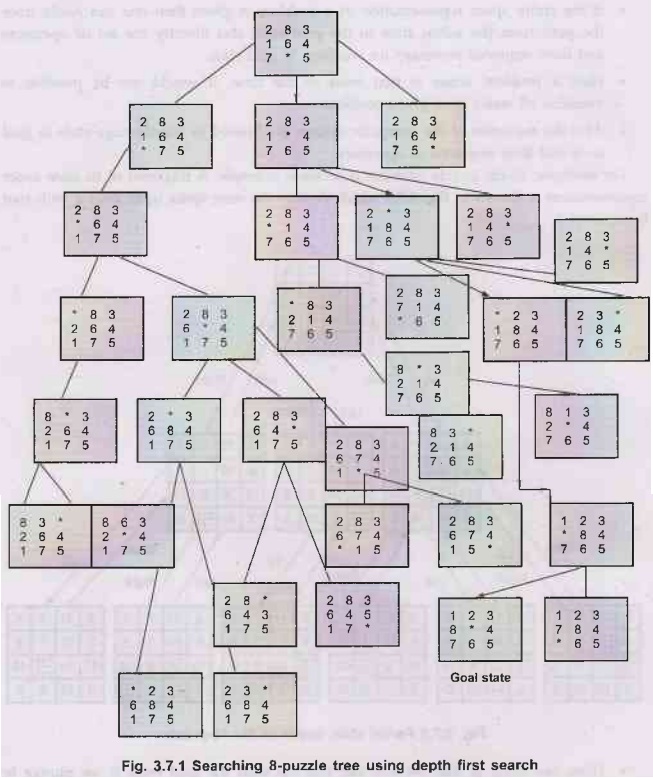
Example 3.7.2 Give DFS for 8 puzzle problem.

A search tree produced by depth first search for 8-puzzle problem.

(See Fig. 3.7.1 on next page).

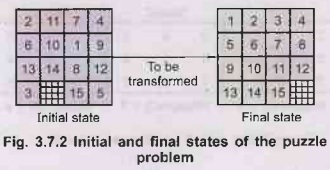
Example 3.7.3 Give a state space representation of 15 puzzle problem.

Solution:

• In 15 puzzle problem, we have a square frame containing 15-tiles and an empty slot, i.e., total 16 subsquares. The tiles are numbered from 1 to 15. We can move the tiles in square frame by moving a tile into empty slot.

• The goal state is one having the tiles in numerical order with the last square an empty slot as shown in Fig. 3.7.2.

• Initial and final states are shown in Fig. 3.7.2. And the operators for this problem are -

UP - If the hole is not touching the top frame, move it up.

DOWN - If the hole is not touching the bottom frame, move it down.

LEFT - If the hole is not touching the left frame, move it left.

RIGHT - If the hole is not touching the right frame, move it right.

• In state space representation we have all possible set of states for a given problem. Or state space is a directed graph with all the states as nodes.

• A node is said to exist if it is possible to obtain it from the initial state by application of a set of operators.

• One can reach to another state or another node by applying an operator on first state.

• If the entire space representation of a problem is given then one can easily trace the path from the initial state to the goal state and identify the set of operators and their sequence necessary for reaching to goal state.

• Here a problem arises is that most of the time, it would not be possible to visualize all states for a given problem.

• Also the resources of the computer system are limited to handle huge state to goal state and their sequence of operators.

For example, 15-tile puzzle problem is a classic example. A fragment of its state space representation is shown in Fig. 3.7.3 which depicts the state space upto level 2 with root being level 0.

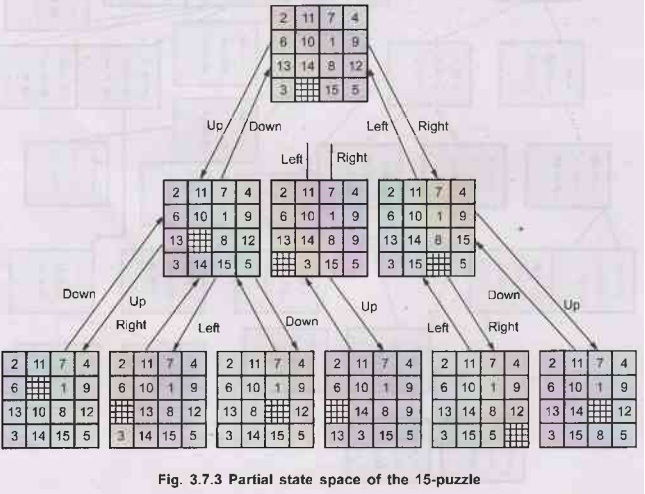
• Here, the irony is that we will not end up with the goal even if we plunge to another level also.

Example 3.7.4 Give state space representation for the farmer, wolf, goat and cabbage problem stated below -

A farmer with his wolf, goat and cabbage come to the edge of a river, they wish to cross - There is a boat at the rivers edge, but only the farmer can row, the boat can carry two things at a time (including the rower). If the wolf is ever left alone with the goat, the wolf  will eat the goat, similarly, if the goat is left alone with the cabbage, the goat will eat the cabbage. Give the search tree and identify a sequence of crossing of the river so that all four characters arrive safely on the other side of the river.

Solution:

• There are 16 subsets of the man (M), wolf (W), goat (G) and cabbage(C).

• Each state corresponds to the subset that is on the left bank states are labeled by hyphenated pairs such as MG-WC, where the symbols to the left of the hyphen denote the subset on the left bank; symbols to the right of the hyphen denote the subset on the right bank.

• Some of the 16 states such as CG-MW, are fatal and may never be entered by the system.

The "inputs" to the system are the actions the man takes. He may cross alone (input M), with the wolf (input W), the goat (input G), or cabbage (input C).

The initial state is MWGC - and the state is - MWGC.

• Sequence of crossing of the river so that all four characters arrive safely is -

i) First man cross the river with goat.

ii) Man come back.

iii) Man takes either cabbage (or wolf) with him to another side.

iv) Man comes back with goat to first side.

v) Man takes wolf (or cabbage) with him him to another side.

vi) Man comes back.

vii) Man takes goat with him to another back.

This sequence is shown by dark lines in Fig. 3.7.5.

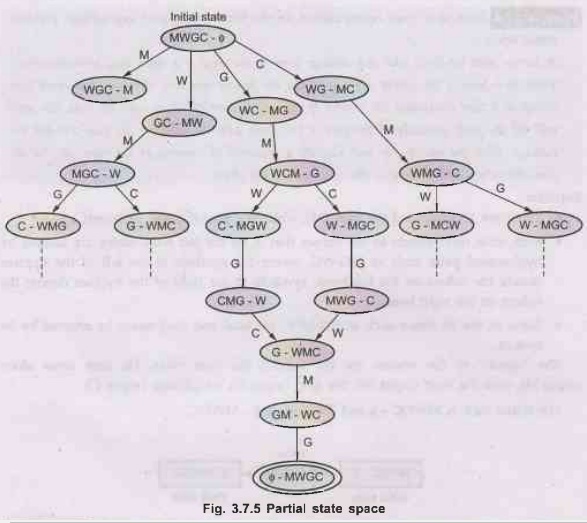
Example 3.7.5 Consider the missionaries and cannibals problem. Analyze this problem with respect to seven problem characteristics and find a good state space representation.

Solution:

• The missionaries and cannibals problem - Three missionaries and three cannibals find themselves on one side of a river. They have agreed that would all like to get to the other side. But missionaries are not sure what else the cannibals have agreed to, so missionaries want to manage the trip across the river in such a way that number of missionaries on either side of the river is never less than the number of cannibals who are on the same side. The only one boat available hold only two people at a time. How can everyone get across the river without missionaries risking being eaten?

• Analysis of problem with respect to problem characteristics - It encompasses a variety of specific technique, each of which is particularly effective for a small class of problem. In order to choose most appropriate method, it is necessary to analyze along seven key dimension -

1) Is the problem decomposable into a set of independent smaller or easier subproblem?

The missionaries and cannibals problem is not decomposable because here every movement of either missionaries or cannibals effect next movement missionaries or cannibals. If one try to decompose it, he will unable to get any subproblem which is independent of others.

2) Can solution steps be ignored or at least undone if they prove? unwise. Here many solution steps in the problem are ignored or undone when they proved unwise. undone when they proved unwise. In missionaries and cannibals problem, in initial state one have three possible move like, two missionaries move simultaneously to other side, two cannibals move simultaneously to other side, or one cannibal and one missionary can move to other side. In first case, if two missionaries move then the number of cannibals is more than the number of missionaries so this solution step can be ignored or undone. Other two possible moves can be used but second possible move (two cannibals move) will be ignored further.

3) Is the problem universe predictable?

In missionaries and cannibals problem, every time one make a move, one know exactly what will happen. This means that it is possible to plan an entire sequence of move and be confident that we know what the resulting state will be. So, by explaining all the above, it means to say that, here nothing is universe predictable, means result of every possible move is exactly known.

4) Is a good solution to the problem obvious without comparison to all other possible solution?

In the problem there is one and only one good solution to the problem. Hence no need to compare it with other. If there exists more than one path of the solution then one cannot be sure unless we also try all other path to make sure that none of them is more efficient.

5) Is the desired solution a state of the world or a path to a state?

In missionaries and cannibals problem it is not sufficient to report that one has solved the problem and that the final state is reached. Here what we really must report is not the final state but the path that leads to the state. Thus, a statement of a solution to this problem must be a sequence of operations, that produce the final state.

6) Is a large amount of knowledge absolutely required to solve the problem, or is knowledge important only to constraint the search?

Here there is no need of large amount of knowledge. The required knowledge is very little - just the rule for determine the legal moves and some simple control mechanism

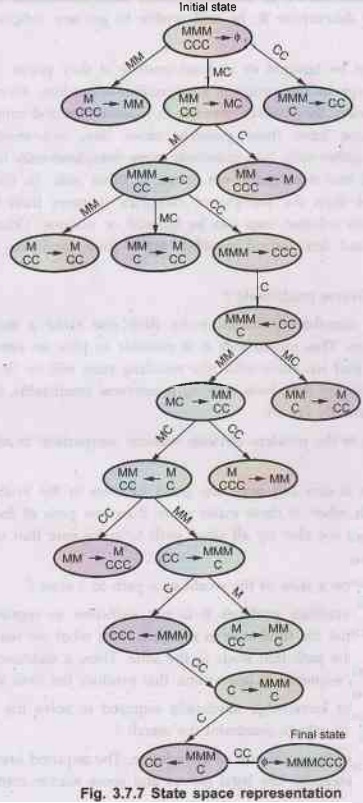
that implements an appropriate search procedure. Additional knowledge about such things as good strategy and tactics could of course help considerably to constraint the search and speed up the execution of the program.

7) Can a computer, given the problem return the solution, or will the solution of the problem require interaction between the computer and person?

In the problem, there is no need of interaction between the computer and person. Here, given the problem, set of rule and a final state it returns the solution with each intermediate step.

• State space representation of missionaries and cannibals problem - In state space representation, every missionary is denoted by M and cannibals is denoted by C. Numbers of M's and C's show the number of missionaries and cannibals. Circle represents the state and arrow represents the forward and backward move.

Example 3.7.6 You are given two jugs, a 4-gallon jug and a 3-gallon jug. Neither has any measuring markers on it. There is a pump that can be used to fill the jug with water. How can you get exactly 2 gallons of water in the 4-gallon jug?

Solution:

• For solving above problem, first of all state space or global database for this problem has to be described as the set of ordered pairs of integers (x, y), such that x = 0, 1, 2, 3 or 4 and y = 0, 1, 2, 3.

• Here, x represents the number of gallons of water in 4-gallon jug and y represents the quantity of water in the 3-gallon jug. The starting state is (0, 0) i.e. no water in both the jugs. And the termination condition or global state is (2, n) i.e., 2 gallon water in 4-gallon jug and n gallon water in 3-gallon jug and here n can have any value as it is not mentioned in the question.

• With the given condition in question, we have to make some more assumptions as -

1) One can fill the jug from a pump any number of times.

2) One can pour the water from one jug to another jug.

3) One can pour the water out of the jug onto the ground.

4) There are no other measuring devices available including no measuring marks available on jugs etc.

Now, further we have some productions rules for water jug problem as given in Fig. 3.7.8.

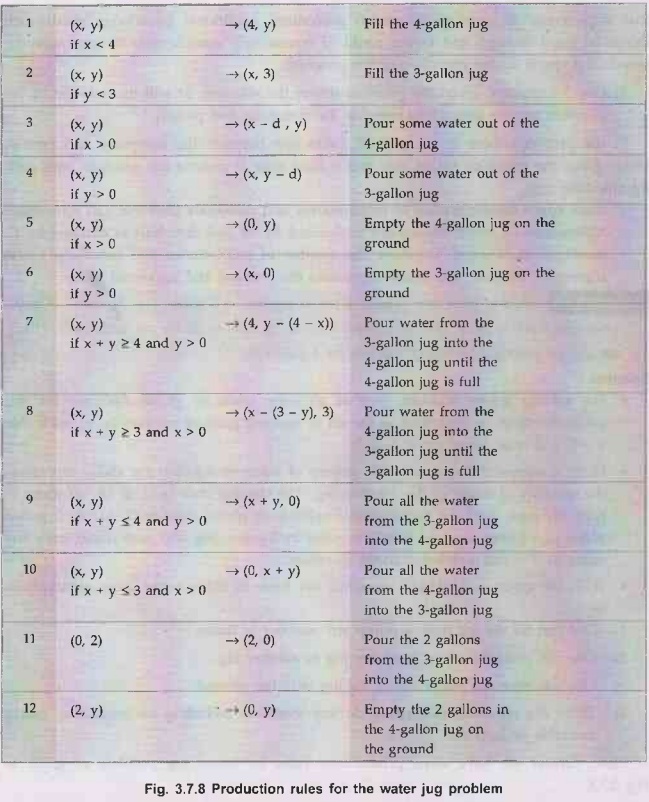
1) Here, the first rule indicates that 4-gallon jug is filled completely as trying to fill a already filled jug is waste.

2) Similarly second rule shows that the 3-gallon jug is filled completely.

3) Third rule indicates that some amount of water (say d) is poured on the ground from 4-gallon jug. So resulting state is (x - d, y).

4) Fourth rule indicates removal of d amount of water from 3-gallon jug. That shows the resulting state (x, y - d).

5) Fifth rule indicates that all the water of 4-gallon jug is poured out onto ground so in resulting state 4-gallon jug is empty (0, y).

6) Similarly as above in sixth rule, 3-gallon jug is made empty (x, 0).

7) Seventh rule shows that, we pour water form 3-galon jug into 4-gallon jug until 4-gallon jug is full.

So, resulting state is (4, y - (4 - x)).

8) Similarly, eight rule shows that water is poured from 4-gallon jug, into the 3-gallon jug until 3-gallon jug is full.

So, resulting state is (x - (3 - y), 3).

9) Nineth rule indicates that all the water from 3-gallon jug is poured into 4-gallon jug considering that x + y ≤ 4.

It results into a final state (x + y, 0).

10) Similarly, tenth rule indicates that all the water is poured from 4-gallon jug into Tog to the 3-gallon jug resulting into a state (0, x + y) considering x + y ≤3.

11) Eleventh rule shows that 3-gallon jug has only 2-gallon water that is poured 2 completely into empty 4-gallon jug.

12) Twelth rule indicates that 2-gallon water from 4-gallon jug is poured out of the jug.

Now we look for the solution of this problem each one operator has to be chosen, from above given operators. These operators will be rules whose left sides are watched against the current state and whose right sides describes the new state that results from applying the rule.

One solution of this problem is given in Fig. 3.7.9.

i. In the initial state, we have two empty jugs - one 4-gallon jug and one 3-gallon jug represented by the state (0, 0).

ii. Now, we fill 3-gallon jug completely by a pipe applying rule 2 resulting into a state (0, 3).

iii. Further we pour all the water from 3-gallon jug into the 4-gallon jug using rule 9 resulting into the state (3, 0)...

iv. Further, again by applying rule 2 we fill the 3-gallon jug full, resulting into the state (3, 3).

v. Now, by applying rule 7 we pour water from 3-gallon jug into 4-gallon jug so that 4-gallon gets full resulting into the state (4, 2).

vi. Further by applying rule 5 or 12 we make 4-gallon jug empty, resulting into the state (0, 2).

vii. Now, by applying rule 9 or 11 we pour all the water from 3-gallon jug into 4-gallon jug resulting into the state (2, 0) i.e., our termination condition or goal state.

Example 3.7.7 Specify a global database, rules and termination condition to solve the given water jug problem.

Given a 5 liters jug filled with water and an empty 2 liter jug, how can one obtain precisely 1 liter in 2 liters jug? Water may either be discarded or poured from one jug to another; however no more than the 5 liter is available?

Solution: For this problem with given conditions, we can make some production rules, which are as follows -

Now, look for the solution of the problem.

Example 3.7.8 Analyze Water jug problem with respect to the seven problem characteristics. Solution Analysis of water jug problem with respect to the seven problem characteristics are as follows-

i. Is the problem decomposable?

In water jug problem, the goal is to get exactly 2 gallons of water in the 4-gallon jug. The idea of this solution is to reduce the problem into two subproblem, which is not possible. Even if one devide it into subproblem, they not independent.

ii. Can solution be ignored or undone?

In our problem suppose program makes a stupid move and realizes it a couple of moves later. It cannot simply play as through it had never made the stupid move. All it can do is to simply back up and start the game over from that point.

iii. Is the problem's universe predictable?

In the problem, every time one make a move one know exactly what will happen. This means that it is possible to plan as entire sequence of move and be confident that are know what the resulting state will be. Hence problem is not universe predictable.

iv. Is a good solution absolute or relative ?

In water jug problem, the goal is to get exactly 2-gallon of water in 4-gallon jug. It does not matter which path one follows or how one got the goal state. If one do follow one path successfully to the answer, there is no reason to go back and see if some other path might also lead to a solution. Hence the good solution is absolute.

v. Is the solution a state or a path?

Here the solution is state in which 4-gallon jug is filled with exactly 2-gallon water, but the way or path does matter.

vi. What is the role of knowledge?

In water jug problem, the knowledge required is, just the set of rules for determining legal move and some simple control mechanism that implement an appropriate search procedure.

vii. Does the task require interaction with a person.

The problem does not require any interaction with a person. It just requires problem, set of rules and a goal state at the initial stage. Now between execution no knowledge and no interaction with person is required.

Example 3.7.9 Analyze travelling salesman problem with respect to the seven problem characteristics.

Solution: Analysis of TSP with respect to seven problem characteristics are as follows –

i. Is the problem decomposable?

This problem is not decomposable. In this problem, the goal is to find shortest path that visit each city exactly once, and hence whole problem will be considered simultaneously.

ii. Can solution steps be ignored or undone?

In TSP suppose program makes a stupid move means choose the path which is not a shortest path and realizes it a couple of move later. It cannot simply go further as through it had never made wrong move. All it can do is to start the game again and try to make the best of the current situation and go on from there. So solution steps cannot be ignored or undone.

iii. Is the universe predictable?

In travelling salesman problem, every time one choose a city it is know exactly which will be the next choice, because here all the distance between each cities are known. So here it is possible to plan an entire sequence of move. One can use planning to avoid having to undo actual move. So there is nothing universe predictable.

iv. Is a good solution absolute or relative?

In the problem, goal is to find the shortest route that visit each city exactly once, suppose cities to be visited and distance between them are shown in Fig. 3.7.12.

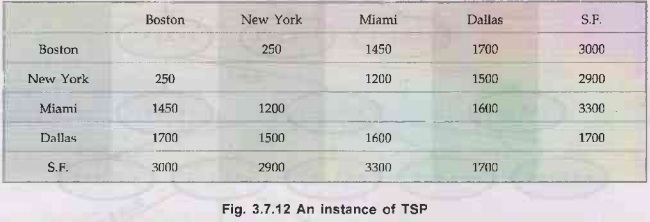
One place the salesman could start, is Boston. Now the next city he has to visit cannot be sure unless we also try all other path to make sure that none of them is shorter. Hence, the good solution is relative but not absolute.

i. Is the solution a state or a path?

The goal of the problem is to find the shortest path that visit each city exactly once. For this type of problem one really must report is not the final state but the path one found to that state. Thus, a statement of a solution to this problem must be a sequence of operations that produces the final state.

ii. What is the role of knowledge?

The required knowledge is just the knowledge of the cities to be visited, the distance between these cities and some simple control mechanism that implement an appropriate search process.

iii. Does task require interaction with a person.

In travelling salesman problem, there is no need to interact with person.

Example 3.7.10 Give state-space representation of the following

i) Water jug problem

Solution: i) Water jug problem - State space representation of water jug problem is given below according to the twelve possible rules.

For all the production rules of water jug problem refer to example 3.7.6.

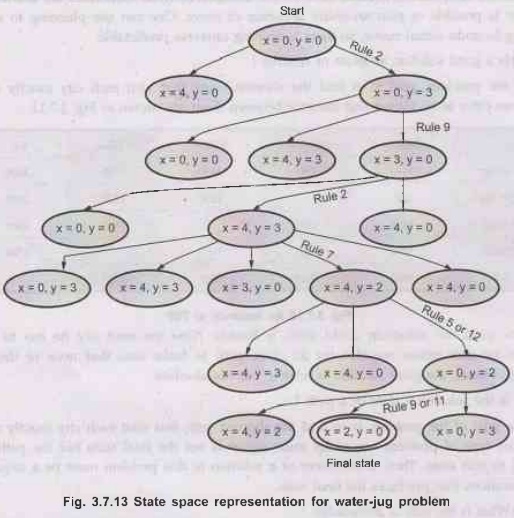
• Each state in state space representation is denoted as (x, y).

• Here x is an 4-gallons jug while y is an 3-gallons jug. Value in place of x denotes the amount of water in 4-gallons jug and value of y denotes amount of water in 3-gallons jug.

• Each state enclosed within a circle shows the resultant state after application of appropriate rule on that state.

• Initial state is represented as start state while final state is enclosed within double circle.

Example 3.7.11 Three pegs labeled A, B and C are given in which peg A has finite number of disks (n) with decreasing size. The task of the game is to move the disks from peg A to peg C using peg B as an auxiliary. The rules of the game are as follows:

i) Only one disk may be moved at a time specifically, only the top disk on any peg may be moved to any other peg.

ii) At any time the large disk can't be placed on a smaller disk.

Solve the problem and describe the following terms:

a) State b) Initial state c) Goal state d) Operators e) Solution.

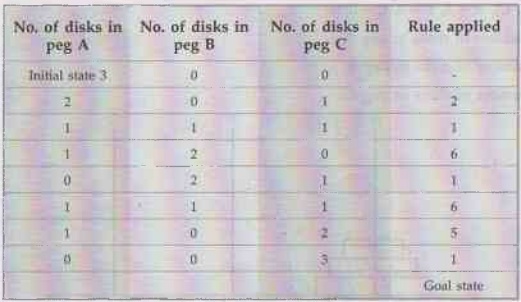
Solution: a) State:

{(A, B, C), A = 3, B = 0, C = 0}

A Number of disks in peg A

B - Number of disks in peg B

C - Number of disks in peg C

b) Initial state:

{(A, B, C) = (3, 0, 0)}

c) Goal state:

{(A, B, C) = (0, 0, 3)}

d) Operators:

Condition: Each move operation is performed with a condition that no larger disk can be placed on a smaller disk.

e) Solution:

Example 3.7.12 Give the initial state, goal test, successor function and cost function for each of the following. Choose a formulation that is precise enough to be implemented.

a) You have to color a planner map using only four colors, in such a way that no two adjacent regions have the same color.

b) A 3-feet tall monkey is in a room where some bananas are suspended from the 8-feet ceiling. He would like to get the bananas. The room contains two stackable, movable, climable 3-feet-high crates.

c) You have a program that outputs the message "illegal input record" when fed a certain file of input records. You know that processing of each record is independent of the other records. You want to discover what record is illegal.

d) You have three jugs, measuring 12 gallons, 8 gallons and 3 gallons and a water fancet. You can fill the jug up or empty them out from one to another or onto the ground. You need to measure out exactly one gallon.

Solution:

a) Initial state: No regions colored

Goal test: All regions colored, and no two adjacent regions have the same color.

Successor function: Assign a color to a region.

Cost function: Number of assignment.

b) Initial state: Monkey is in a room, where some bananas are hanging on the ceiling.

Goal test: Monkey has bananas.

Successor function: Hop on crate; Hop off crate; push crate from one step to another; walk from one step to another; grab bananas (if standing on crate)

Cost function: Number of actions.

c) Initial state: Considering all input records.

Goal test: Considering all input records.

Successor function: Run all the records sequentially.

Cost function: A single record, which gives "illegal input" message.

d) Initial state: Jugs have values [0, 0, 0]

Successor function: Given values [x, y, z], generates [12, y, z], [x, 8, z], [x, y, 3] (by filling); [0, y, z], [x, 0, z], [x, y, 0] (by emptying); or for any two jugs with current values x and y, pour y into x, this changes the jug with x to the minimum of x + y and the jug with y decrements by the amount gained by the first jug.

Goal state: Fill the 12 gallon jug, from this fill the other 2 jugs with 8 gallon and 3 gallon you will get exactly one gallon of water in the first jug.

Cost function: Number of actions.

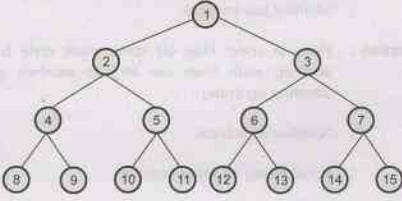
Example 3.7.13 Consider a state space where the start state is number 1 and the successor function for state n returns two states, numbers 2n and 2n + 1.

a) Draw the portion of the state space for states 1 to 15.

b) Suppose the goal state is 11 list the order in which nodes will be visited for breadth-first search with limit 3 and iterative deepening search.

c) Would bidirectional search be appropriate for this problem? If so, describe in detail how it would work.

d) What is the branching factor in each direction of the bidirectional search?

e) Does the answer to (c) suggest a reformulation of the problem that would allow you to no solve the problem of getting from state 1 to a given goal state with almost no search.

Solution: 

a) State space:

b)Breadth-first search: 1 2 3 4 5 6 7 8 9 10 11

Depth limited search: 1 2 4 89.5 10 11

Iterative deepening search: 1; 1 2 3; 1 2 4 5 3 6 7;

1 2 4 8 9 5 0 11

c) Bidirectional search is very useful, because search done in both the directions at the same time.

d) 2 in the forward direction; 1 in the reverse direction.

e) Yes, start at the goal, and apply the single reverse successor action until you reach 1.

Example 3.7.14 Consider a sliding block puzzle with the following initial configuration. There are three black tiles (B), three white tiles (W) and an empty cell (E). The puzzle has the following moves

• A tile may move into an adjacent empty cell with unit cost

• A tile may hop over at most two other tiles into an empty cell with a cost equal to the number of tiles hopped over

The goal of the puzzle is to have all of the white tiles to the left of all of the black tiles. (without regard to position of empty cell.)

Solution: The goal configuration is

The heuristic function is

g' is 1 for every level of the tree

X → number of tiles hopped over

Y→ number of tiles out of place.

h' = X + Y

f ' = g'+h'

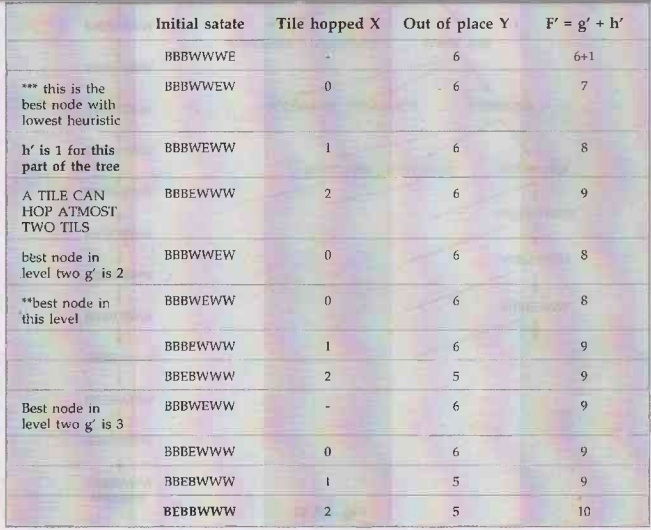
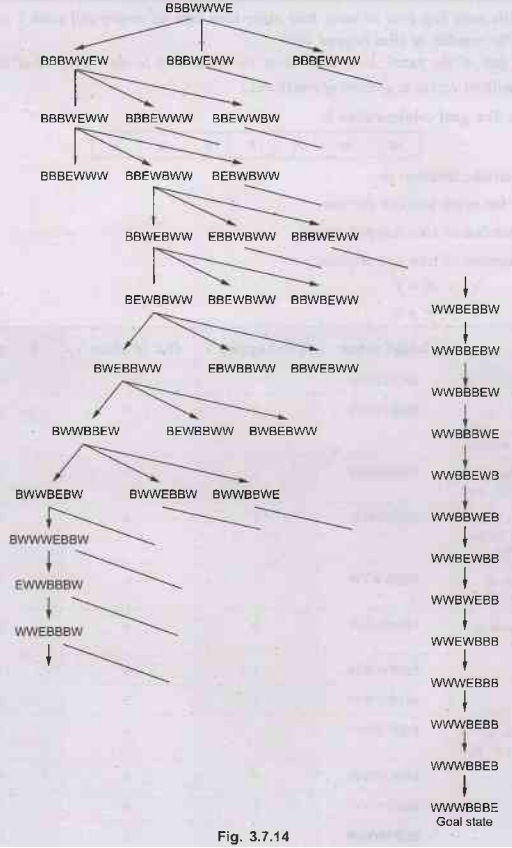
The search continues in this way and the search tree is as follows in Fig. 3.7.14.

Example 3.7.15 Give the breadth-first search, depth-first search, depth-limited search (limit = 2) and iterative deepening search and list the name of the nodes in order by the algorithms for the search of node C in the search space showing figure. AU: Dec.-10, Marks 16

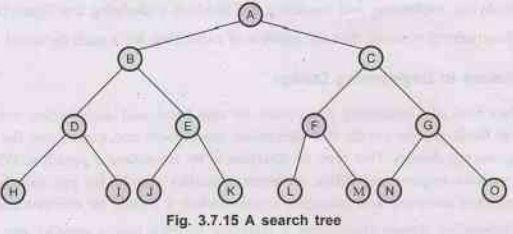
Solution: Following is the node list in which nodes are listed according to the order, the algorithm will visit them.

1) BFS

A, B, C, D, E, F, G, H, I, J, K, L, M, N, O.

2) DFS

A, B, D, H, I, E, J, K, C, F, L, M, G, N, O.

3) DLS (limit= 2)

A, B, D, E, C, F, G.

4) IDDFS

(It searches in DLS manner until goal is not reached).

(Assuming goal node is not specified in the given node tree then IDDS will search in following manner).

Limit = 0

A

Limit = 1

A, B, C.

Limit = 2

A, B, D, E, C, F, G.

Limit = 3

A, B, D, H, I, E, J, K, C, F, L, M, G, N, O.

(It continues to next level till no goal state is reached).