Searching for Solution

Searching for Solution

AU Dec.-10, 14, May-14

For finding the solution one can make use of explicit search tree that is generated by the initial state and the successor function that together define the state space. In general, we may have search graph rather than a search tree as the same state can be reached from multiple paths.

"A set of all possible states for a given problem is known as the state space of the problem".

Consider a example of making a coffee:

If one wants to make a cup of coffee, then state space representation of this problem can be done as follows:

1) Analyze the problem, i.e., verify whether the necessary ingredients like instant coffee powder, milk powder, sugar, kettle, stove etc., are available or not.

2) If ingredients are available then steps to solve the problem are -

i) Boil half cup of water in the kettle.

ii) Take some of the boiled water in a cup add necessary amount of instant coffee powder to make decoction.

iii) Add milk powder to the remaining boiling water to make milk.

iv) Mix decoction and milk.

v) Add sufficient quantity of sugar to your taste and the coffee is ready.

3) Now, by representing all the steps done sequentially we can make state space representation of this problem as shown in Fig. 3.3.1.

4) Westarted with the ingredients (initial state), followed by a sequence of steps (called states) and at last had a cup of coffee (goal state).

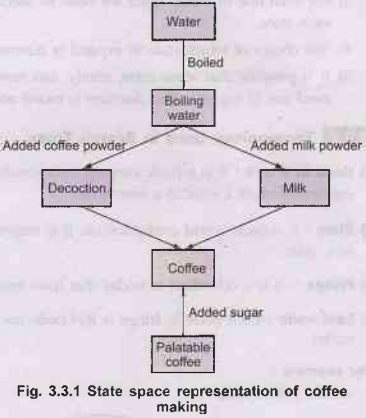
We added only needed amount of coffee powder, milk powder and sugar (operators). Thus, every AI problem has to do the process of searching for the solution steps as they are not explicit in nature. This searching is needed for solution steps are not known beforehand and have to be found out. Basically to do a search process, the following are needed -

i) The initial state description of the problem.

ii) A set of legal operators that changes the state.

iii) The final or the goal state.

Given these, searching can be defined, as a sequence of steps that transforms the initial state to the goal state. In other words, we can say that a problem can be defined as a state space search.

Construction of State Space

1) The root of search tree is a search node corresponding to initial state. In this state only we can check if goal is reached.

2) If goal is not reached we need to consider another state. Such a can be done by to expanding from the current state by applying successor function which generates new state. From this we may get multiple states.

3) For each one of these, again we need to check goal test or else repeat expansion of each state.

4) The choice of which state to expand is determined by the search strategy.

5) It is possible that some state, surely, can never lead to goal state. Such a state we need not to expand. This decision is based on various conditions of the problem.

Terminology used in Search Trees

1) Node in a tree: It is a book keeping data structure to represent the structure configuration of a state in a search tree.

2) State: It reflects world configuration. It is mapping of state and action to another new state.

3) Fringe: It is a collection of nodes that have been generated but not yet expanded.

4) Leaf node: Each node in fringe is leaf node (as it does not have further successor node).

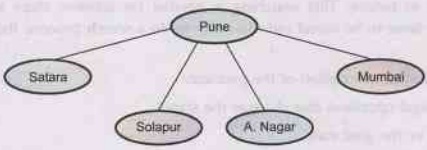
For example:

a) The initial state

b) After expanding Pune

c) After expanding Satara

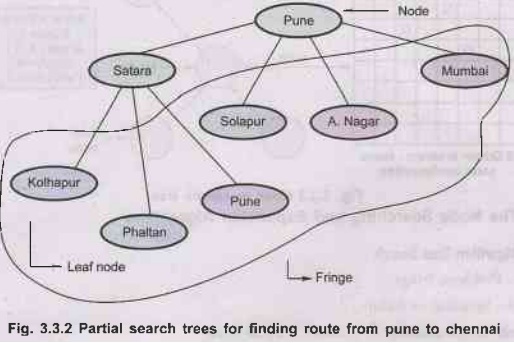
5) Search strategy: It is a function that selects the next node to be expanded from current fringe. Strategy looks for best node for further expansion.

For finding best node each node needs to be examined. If fringe has many nodes then it would be computationally expensive.

The collection of un-expanded nodes (fringe) is implemented as queue, provided with, the sets of operations to work with queue. These operations can be CREATE Queue, INSERT in Queue, DELETE from Queue and all necessary operations which can be used for general tree-search algorithm.

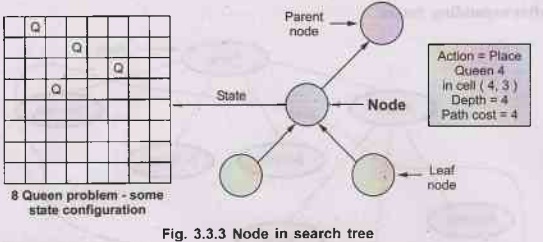
Node Representation in a Search-Tree

Formally we can represent the node of search tree with 5 components,

1) State: The state, in the state space to which the node corresponds;

2) Parent-node: The node in the search tree that generated this node;

3) Action: The action that was applied to the parent to generate the node;

4) Path-cost: The cost, traditionally denoted by function g(n), of the path, from the initial state to the node, as indicated by the parent pointers;

5) Depth: The number of steps along the path from the initial state.

The Node Searching and Expansion Algorithms

1. Algorithm Tree Search

Input - Problem, fringe.

Output - Solution or failure.

1) Create initial node from problem's initial state.

2) Create fringe from initial node.

3) If fringe is empty return failure.

4) Node = first_node from_fringe.

5) If Goal test succeeds on node then return solution (node).

6) Expand node and add the newly generated nodes to fringe.

7) Repeat step (3) to (6).

2. Algorithm Expand Node

/* This algorithm will be used in Tree search for expanding the node */

Input Node, problem

Output - A set of nodes (newly generated) (successor)

1) Initial successor set is empty.

2) For each <action, result>,

in successor function of a problem for a given state do steps (3) to (9).

3) s = a new node.

4) STATE [s] = result.

5) Parent Node [s] = node.

6) Action [s] = action.

7) Path Cost [s] = PathCost [node] + StepCost (node, action s).

8) Depth [s] = Depth [node] + 1.

9) Add s to successor set.

10) Return successor set.

Measuring Problem Solving Performance

When we are solving a problem we have three possible outcomes 1) We reach at failure state 2) Solution state 3) Algorithm might get stuck in an infinite loop.

Problem solving algorithm's performance can be evaluated on the basis 4 factors-

1) Completeness:

Does the algorithm surely finds a solution, if really the solution exists.

2) Optimality:

Some times it happens that there are multiple solutions to a single problem. But the algorithm is expected to produce best solution among all feasible solution, which is called as optimal solution.

3) Time complexity: How much time the algorithm takes to find the solution.

4) Space complexity: How much memory is required to perform the search algorithm.

• Major factors affecting time complexity and space complexity.

• Time and space complexity are majorly affected by the size of the state space graph, because it is the input to the algorithm. State space graph needs to be stored as well as it needs to be processed. So it is straight forward that more complex state space graph more is the space and time required.

• The state space graphs complexity is affected by 3 factors-

a) Branching factor:

It is maximum number of successors of any node. If this value is less then less nodes will have to be search, there by getting result fast.

b) Depth of goal node:

It is the depth of the shallowest goal node, where one can reach fast. If this value is small we will get goal node early.

c) Maximum length of path:

It is maximum length of any path in the state space. If length value is more, complexity of state space is more. This is often measured in terms of number of nodes generated.

The major activity in searching is node expansion. The time taken for this is called as search cost. Search cost will typically depend on time complexity.

• Path cost:

Is time bound cost which is incurred for reaching or going to a particular node.

The total cost for algorithm is the combined cost of search cost and the path cost of the solution found along with memory usage.

Total cost = Search cost + Path cost + Memory usage.

For the problem of finding a route from Pune to Chennai, the search cost is amount of time taken by the search and the solution cost is the total length of the path.

The cost found will be helpful for agent to find shorter paths (low cost paths).