Searching

UNIT V

CHAPTER : 6 : Searching and Sorting

6.1 Searching

• When we want to find out particular record efficiently from the given list of elements then there are various methods of searching that element. These methods are called searching methods. Various algorithms based on these searching methods are known as searching algorithms.

• The basic characteristic of any searching algorithm is

i. It should be efficient

ii. Less number of computations must be involved in it.

iii. The space occupied by searching algorithms must be less.

•The most commonly used searching algorithms are -

i.Sequential or linear search

ii. Indexed sequential search

iii. Binary search

• The element to be searched from the given list is called the key element. Let us discuss various searching algorithms.

Linear Search

•Linear search or sequential search is technique in which the given list of elements is scanned from the beginning. The key element is compared with every element of the list. If the match is found the searching is stopped otherwise it will be continued to the end of the list.

•Although this is a simple method, there are some unnecessary comparisons involved in this method.

•The time complexity of this algorithm is O(n). The time complexity will increase linearly with the value of n.

• For higher value of n sequential search is not satisfactory solution.

Example

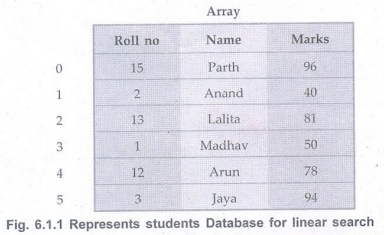
From the above Fig. 6.1.1 the array is maintained to store the students record. The record is not sorted at all. If we want to search the student's record whose roll number is 12 then with the key-roll number we will see the every record whether it is of roll number We can obtain such a record at Array [4] location.

Let us implement the sequential search using C program

'C' Program:

/**********************************************************

Program to perform the linear search operation on some number of elements.

**********************************************************/

#include <stdio.h>

#include<conio.h>

#define MAX 10

int a[MAX],n,i;

/*

The create Function

Input :none

Output:none

Called By: main

Calls:none

*/

void create()

{

printf("\n How Many Elements");

scanf("%d", &n);

printf("\n Enter The Elements");

for(i=0;i<n;i++)

scanf("%d",&a[i]);

}

/*

The display Function

Input:none

Output:none

Called By:main

Calls:none

*/

void display()

{

printf("\n The Elements Are");

for(i=0;i<n;i++)

printf("\n%d",a[i]);

}

/*

The search function

Input:key element- which is to be searched

Output:the status

Called By:main

Calls:none

*/

search(int k)

{

for(i=0;i<n;i++)

{

if(a[i]==k)

return 1;

}

return 0;

}

void main()

{

int status,key;

clrscr();

create();

display();

printf("\n Enter the Element Which You wish to Search ");

scanf("%d",&key);

status search(key);

if (status == 1)

printf("\n The Element is Present");

else

printf("\n The Element Is Not Found");

getch();

}

/***************End Of Program******************/

How Many Elements 5

Enter The Elements 10

1

100

1000

10000

The Elements Are

10

1

100

1000

10000

Enter the Element Which You wish to Search 99

The Element Is Not Found

How Many Elements 5

The Elements Are 10

1

100

1000

10000

The Elements Are

10

1

100

1000

10000

Enter the Element Which You wish to Search 100

The Element is Present

Advantages of linear searching

1. It is simple to implement.

2. It does not require specific ordering before applying the method.

Disadvantage of linear searching

1. It is less efficient..

Binary Search

Definition: Binary search is a searching technique in which the elements are arranged in a sorted order and each time mid element is compared with the key element recursively.

Example:

The necessity of this method is that all the elements should be sorted. So let us take an array of sorted elements.

Step 1: Now the key element which is to be searched is = 99. key = 99.

Step 2: Find the middle element of the array. Compare it with the key

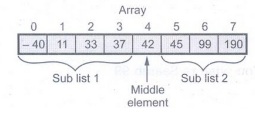
if middle? Key

i.e.if 42 ? 99

if 42 < 99 search the sublist 2

Now handle only sublist 2. Again divide it, find mid of sublist 2

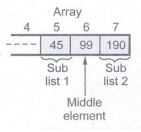
if middle? Key

i.e.if 99 ? 99

So match is found at 7^th position of array i.e. at array [6]

Thus by binary search method we can find the element 99 present in the given list at array [6]th location.

Non Recursive Binary Search Program

/****************************************************************

Implementation of non recursive Binary Search algorithm

****************************************************************/

#include<stdio.h>

#include<conio.h>

#define SIZE 10

int n;

void main()

{

int A[SIZE],KEY,i,flag;

int BinSearch(int A[SIZE],int KEY);

clrscr();

printf("\n How Many elements in an array?");

scanf("%d", &n);

printf("\n Enter The Elements");

for(i=0;i<n;i++)

scanf("%d", &A[i]);

printf("\n Enter the element which is to be searched");

scanf("%d", &KEY);

flag BinSearch(A,KEY);

if(flag==-1)

printf("\n The Element is not present");

else

printf("\n The element is at A[%d] location",flag);

getch();

}

int BinSearch(int A[SIZE], int KEY)

{

int low,high,m;

low=0;

high-n-1;

while(low<=high)

{

m= =(low+high)/2; //mid of the array is obtained

if(KEY==A[m])

return m;

else if(KEY <A[m])

high=m-1; //search the left sub list

else

low=m+1; //search the right sub list

}

return-1; //if element is not present in the list

}

Output (Run 1)

How Many elements in an array? 6.

Enter The Elements

10

20

30

40

50

60

Enter the element which is to be searched 50

The element is at A[4] location

(Run 2)

How Many elements in an array? 5

Enter The Elements

10

20

30

40

50

Enter the element which is to be searched 80

The Element is not present

Algorithm For Binary Search Using Recursive definition :

1. if(low>high)

2. return;

3. mid (low+high)/2;

4. if(x==a[mid])

5.return (mid);

6. if(x<a[mid])

7. search for x in a[low] to a[mid-1];

8.else

9. search for x in a[mid+1] to a[high];

Recursive Binary Search Program

/**********************************************************

Program for searching the number by Binary Search. The list of numbers should be in ascending order. The program also shows the location at which the number is present(if at all)

*********************************************************/

#include<stdio.h>

#include<conio.h>

#include<stdlib.h>

#define size 10

*/

The binsearch Function

Input:array of elements, key element,

starting and ending element of the list

i.e.a,x,low and high.

Output:location at which the number can be present

Called By:main

Calls:itself

*/

int binsearch(int a[], int x,int low,int high)

{

int mid;

if(low>high)

return(-1);

mid = (low+high)/2;

if(x == a[mid])

return(mid);

else if(x<a[mid])

binsearch(a,x,low,mid-1);

else

binsearch(a,x,mid+1,high);

}

/*

The main Function

Input:none

Output:none

Called By:O.S.

Calls:binsearch

*/

void main(void)

{

int n,i,low,high, a[size],key,ans;

clrscr();

printf("\n\t\t\t Binary Search Method ");

printf("\n Enter the total number of elements");

scanf("%d", &n);

printf("\nEnter the list of elements");

for(i=0;i<n;i++)

scanf("%d",&a[i]);

low =0;

high = n-1;

printf("\n Enter the element which you want to search");

scanf("%d", &key);

ans=binsearch(a,key,low,high);

if(ans!= -1)

printf("\n The number %d is present in the list at location %d", key,ans+1);

else

printf("\n The number is not present in the list");

getch();

}

/************** End Of Program********************/

Output

Binary Search Method

Enter the total number of elements 5

Enter the list of elements

10

20

30

40

50

Enter the element which you want to search 40

The number 40 is present in the list at location 4

Linear Search Vs. Binary Search

Review Questions

1. Explain binary searching.lt ekst

2. Write the difference between binary search and linear search.

 3. Write a C function to find the element using linear search.

 4. Write a C program to search a number with the given set of numbers using binary search.

5. Distinguish between linear search and binary search. State and explain the algorithms for both the search with example.

6. Write an algorithm for binary search with suitable example.