Rules of Inference for Quantifierd Statements

Rules of Inference for Quantifierd statements

Rules of inference

Rule P:

A given premise may be introduced at any stage in the derivation.

Rule T :

A formula S may be introduced in a derivation if S is tautologically implied by one or more of the preceeding formulae in the derivation.

Rupe CP:

If we can drive S from R and a set of given premises, then we can derive R→S from the set of premises alone.

Rules in Quantifiers

Rule US :  (Universal Specification)

From (x) A(x) one can conclude A(y)

If a statement of the form (∀x) (A(x)) is assumed to be true, then the universal quantifier can be dropped to obtain A(y) is true for any arbitrary object 'y' in the universe.

Rule ES : [Existential Specification]

From (Ǝx) A(x) one can conclude A(y) provided that y is not free in any given premise and also not free in any prior step of the derivation. These requirements can easily be met by choosing a new variable each time ES is used.

Note: The conditions of ES are more restrictive than ordinarily required, but they donot affect the posibility of deriving any conclusion.

Rule : EG [Existential Generalization]

From A(x) one can conclude (Ǝy) A(y).

If A(x) is true for some element x in the universe, then (Ǝ(y)) A(y) is true

Rule : UG (Universal Generalization)

From A(x) one can conclude (y) A(v) provided that x is not free in any of the given premises and provided that if x is free in a prior step which resulted from use of ES, then no variables introduced by that use of ES appear free in A(x)

Example 1.

Let D(u, v): u is divisible by v.

S = {5, 7, 10, 11}

Then the statement (Ǝu) D(u, 5) is true because D(5, 5) and D(10, 5) are true.

On the other hand, (v) D(v, 5) is false because D(7, 5) and D(11, 5) are false.

Consider now the following derivation:

{1} (1) (u) D(u, 5)   P

{1} (2) D(x, t)   ES, (1)

{1} (3) (v) D(y, 5)             UG, (2), neglecting the second restriction.

In step 3, we have obtained from D(x, 5) the conclusion (y) D(y, 5). Obviously x is not free in the premise and so the first restriction is satisfied. But x is free in step 2 which resulted by the use of ES, and that x has been introduced by the use of ES and appears free in D(x, 5); hence it cannot be generalized. Thus we have obtained a false conclusion from the true premise.

Example 2. Show that (x) (H(x) → M(x)) ^ H(s) ⇒ M(s). Note that this problem is a symbolic translation of a well-known argument known as the "Socrates argument" which is given by :

All men are mortal.

Socrates is a man.

Therefore Socrates is a mortal.

If we denote H(x): x is a man, M(x): x is a mortal, and s : Socrates, we can put the argument in the above form.

Solution :

{1} (1) (x) (H(x) → M(x))     P

{1} (2) H(s) → M(s)      US, (1)

{3} (3) H(s)      P

{1,3} (4) M(s)      T, (2), (3), I₁₁

Note that in step 2 first we remove the universal quantifier.

Example 3. Show that (x) (P(x) → Q(x)) ^ (x) (Q(x) → R(x)) ⇒ (x) (P(x) →  R(x))

Solution:

{1} (1) (x) (P(x) → Q(x))      P

{1} (2) P(y) → Q(y)      US, (1)

{3} (3) (x) (Q(x) → R(x))     P

{3} (4) Q(y) → R(y)      US, (3)

{1,3} (5) P(y) → R(y)      T, (2), (4), I₁₃

{1,3} (6) (x) (P(x)→ R(x))      UG, (5)

Example 4. Show that (Ǝx) M(x) follows logically from the premises (x) (H(x) -> M(x)) and (Ǝx) H(x)

Solution :

{1} (1) (Ǝx) H(x)    P

{1} (2) H(y)    ES, (1)

{3} (3) (x) (H(x) → M(x))    P

{3} (4) H(y) M(y)     US, (3)

{1,3} (5) M(y)     T, (2), (4), I₁₁

{1,3} (6) (Ǝx) M(x)      EG, (5)

Note that in step 2 the variable y is introduced by ES. Therefore a conclusion such as (x) M(x) could not follow from step 5 because it would violate the rules given for UG.

Example 5. Prove that (Ǝx) (P(x)^Q(x)) ⇒ (Ǝx) P(x)^( Ǝx) Q(x) Solution :

[A.U A/M 2005]

{1} (1) (x) (P(x) ^ Q(x))      P

{1} (2) P(y) ^ Q(y)        ES, (1), y fixed

{1} (3) P(y)   T, (2), I₁

{1} (4) Q(y)    T, (2), I₂

{1} (5) (Ǝx) P(x)     EG, (3)

{1} (6) (Ǝx) Q(x)      EG, (4)

{1} (7) (Ǝx) P(x) ^ (Ǝx) Q(x)    T, (4), (5), I₉

Example 6. Show that from

(a) (Ǝx) (F(x) ^ S(x)) → (y) (M(y) → W(y))

(b) (Ǝy) (M(y) ^ ┐W(y)) the conclusion (x) (F(x) → ┐S(x)) follows.

Solution :

{1} (1) (Ǝy) (M(y) ^ ┐W(y))     P

{1} (2) M(z) Ʌ ┐W(z)     ES, (1)

{1} (3) ┐(M(z) -> W(z))      T, (2), E₁₇

{1} (4) (Ǝy) ┐(M(y) → W(y))      EG, (3)

{1} (5) ┐(y) (M(y) → W(y))      E₂₆, (4)

{6} (6) (Ǝx) (F(x)^S(x))→(y) (M(y) → W(y))      P

{1, 6} (7) ┐(Ǝx) (F(x) ^ S(x))       T, (5), (6), I₁₂

{1, 6} (8) (x) ┐(F (x) ^ S(x))        T, (7), E₂₅

{1, 6} (9) ┐(F(a) ^ S(a))     US, (8)

{1, 6} (10) F(a) → ┐S(a)      T, (9), E₉, E₁₆, E₁

{1, 6} (11) (x) (F(x) → ┐S(x))     UG, (10)

Example 7. Show that (x) (P(x) v Q(x)) ⇒ (x)P(x) V (Ǝx) Q(x) (or) (Vx) (P(x) V Q(x)) ⇒ (Vx) P(x) V (Ǝx) Q(x)                       [A.U N/D 2003, M/J 2013]

Solution :

We shall use the indirect method of proof by assuming ┐((x) P(x) v (Ǝx) Q(x)) as an additional premise.

{1} (1) ┐((x) P(x) v (Ǝx) Q(x))               P (assumed)

{1} (2) ┐(x) P(x) ^ ┐(Ǝx) Q(x)               T, (1), E₉

{1} (3) ┐(x) P(x)                  T, (2), I₁

{1} (4) (Ǝx) ┐P(x)               T, (3), E₂₆

{1} (5) ┐(Ǝx) Q(x)              T, (2), I₂

{1} (6) (x) ┐Q(x)                T, (5), R₂₅

{1} (7) ┐P(y)                         ES, (4)

{1} (8) ┐Q(y)                        US, (6)

{1} (9) ┐P(y) ^ ┐Q(y)                    T, (7), (8), I₉

{1} (10) ┐(P(y) v Q(y))                  T, (9), E₉

{11} (11) (x) (P (x) v Q(x))            P

{11} (12) P(y) v Q(y)                  US, (11)

{1, 11)} (13) ┐(P(y) v Q(y)) ^ (P(y) v Q(y))           T, (10), (12), I₉ contradiction

Example 8. There is a mistake in the following derivation. Find it. Is the conclusion valid? If so, obtain a correct deviation.

[1] (1) (∀x) (P(x) → Q(x)               P

[1] (2) P(y) → Q(y)                        US, (1)

[3] (3) (Ǝx) P(x)                             P

[3] (4) P(y)                                     ES, (3)

[1, 3] (5) Q(y)                                T, (2), (4), I₁₁

[1, 3] (6) (Ǝx) Q(x)                        EG, (5)

Solution :

The y introduced in step (2) is free, it should not be introduced again by ES in fourth step. We try to eliminate this mistake by obtaining a correct derivation.

[1] (1) (Ǝx) P(x)                       P

[1] (2) P(y)                               ES, (1)

[3] (3) (∀x) (P(x)) → Q(x))      P

[3] (4) P(y) → Q(y)                 US, (3)

[1, 3] (5) Q(y)                         T, (2), (4), I₁₁

[1, 3] (6) (Ǝx) Q(x)                 EG, (5)

Thus (Ǝx) P(x), (∀x) (P(x) → Q(x)) → (Ǝx) Q(x) is a valid statement.

Example 9. Using CP or otherwise obtain the following implication. (∀x) (P(x) → Q(x)), (∀x) (R(x) → ┐Q(x)) ⇒ (∀x) (R(x) → ┐P(x))         [A.U M/J 2006]

Solution:

[1] (1) (∀x) (P(x) → Q(x))               P

[2] (2) (∀x) (R(x) → ┐Q(x))           P

[2] (3) R(y) → ┐Q(y)                     US, (2)

[4] (4) R(y)                                     P (assumed)

[2, 4] (5) ┐Q(y)                             T, (3), (4)

[1] (6) P(y) → Q(y)                       US, (1)

[1, 2, 4] (7)  ┐P(y)                        T, (5), (6)

[1, 2, 4] (8) R(y) → ┐P(y)            CP, (4), (7)

[1, 2] (9) (∀x) (R(x) → ┐P(x))      UG, (9)

Hence the argument is valid.

Example 10. Is the following conclusion validly derivable from the premises given ?

If (∀x) (P(x) → Q(x)); (Ǝy) P(y), then (Ǝz) Q(z)          [A.U N/D 2012].

Solution :

We use the indirect method, by assuming that the conclusion (Ǝz) Q(z) is false.

[1] (1) ┐(Ǝz) Q(z)                 P (assumed)

[1] (2) (∀z) ┐Q(z)                T, (1)

[3] (3) (Ǝy) P(y)                   P

[3] (4) P(a)                           ES, (3)

[1] (5) ┐Q(a)                       US, (2)

[1, 3] (6) P(a) ^ ┐Q(a)         T, (4), (5)

[1, 3] (7) ┐(P(a) → Q(a))     T, (6)

[8] (8) (∀x P(x) → Q(x))      P

[8] (9) P(a) → Q(a)              US, (8)

[1,3,8] (10) (P(a) → Q(a)) ^ ┐(P(a) → Q(a)    T, (7), (9), contradiction

Example 11. Show that the premises "A student in this class has not read the book", and "Everyone in this class passed the first exam" imply the conclusion" someone who passed the first exam has not read the book".

Solution: Let P(x) : x is in this class

Q(x) : x has read the book

K(x) : x passed the first exam

Step                                   Reason

1. Ǝx (P(x) ^ Q(x))            Premise

2. P(a) ^ ┐Q(a)                  E.S

3. P(a)                               Simplification from (2)

4. ∀x [P(x) → R(x)]          Premise

5. P(a) → R(a)                  U.S from (4)

6. R(a)                              Modus ponens from (3) and (5)

7. ┐Q(a)                           Simplification from (2)

8. R (a) ^ ┐Q(a)               Conjunction from (6) and (7)

9. Ǝx (R(x) ^ ┐Q(x))        E.G from (8)

Formulas involving more than one quantifier

We have discussed so far the appearance of universal or existential quantifier singly. Now we consider cases in which the quantifiers occur in combinations. For example, if P(x, y) is a 2-place predicate formula, then the following possibilities exist.

(x)   (y)           P(x,y)

(Ǝx)   (Ǝy)      P(x, y)

(y)   (Ǝy)        P(x, y)

(Ǝx)   (y)        P(x, y)

It is understood that (x) (y) P (x, y) stands for (x) ((y) P (x, y)) and (Ǝx) (y) P(x, y) for (Ǝx) ((y) P (x, y))

Loot at the following formulae :

(x)   (y)           P(x, y) ↔ (y) (x) P(x, y)        (1)

(x)   (y)           P(x, y) ⇒ (Ǝy) (x) P(x, y)       (2)

(y)   (x)           P (x, y) ⇒ (Ǝx) (y) P(x, y)       (3)

(Ǝy)   (x)         P(x, y) ⇒ (x) (Ǝy) P(x, y)        (4)

(Ǝx)   (y)         P(x, y) ⇒ (y) (Ǝx) P(x, y)       (5)

(x)  (Ǝy)          P(x, y) ⇒ (Ǝy) (Ǝx) P(x, y)     (6)

(y)  (Ǝx)          P(x, y) ⇒ (Ǝx) (Ǝy) P(x, y)     (7)

(Ǝx) (Ǝy)         P(x, y) ⇒ (Ǝy) (Ǝx) P(x, y)      (8)

These implications and equivalences can be put in a figure as follows.

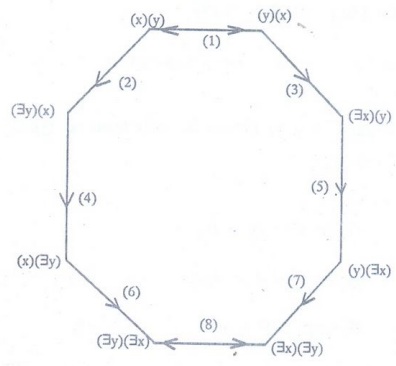
The negation of any of the above formulae can be obtained by repeated applications of the equivalences.

(Ǝx) A(x) ↔ (x) ┐A(x)

┐(x) A(x) ↔ (Ǝx) ┐A(x)

with some care, we have to use the rules US, EG, US and ES.

In the case of US and ES, the specific, variable should be chosen in such a way that it is different from the bound variable used elsewhere.

Consider the formula (x) (Ǝy) P(x, y). Using US, we can write any of the formulae (Ǝy) P(x, y), (Ǝy) P(x, y) but we should not write (Ǝy) P(y, y) because the variable y is used as a bound variable.

i.e., (Ǝy) P(x, y) is not free for y.

Similarly, in using EG, one should be careful. For example, from (x) P(x, y), we can generalise

(Ǝy) (x) P(x, y) or (Ǝz) (x) P(x, z)

but not (Ǝx) (x) P(x, x). Similar care is required in the use of UG and ES.

Example 1. Show that ┐P(a, b) follows logically from (x) (y) (P (x, y) → W(x, y) and ┐W (a, b).

Solution :

{1}   (1)      (x) (y) (P(x, y) → W(x, y)        P

{1}   (2)      (y) (P (a, y) → W(a, y)                  US, (1)

{1}   (3)      P(a, b) → W (a, b)                    US, (2)

{1}   (4)      ┐W(a, b)                                P

{1, 4} (5)    ┐ P(a, b)                              T, (3), (4), I₁₂

Example 2. Write the following statement in the symbolic form : every one who likes fun will enjoy each of these plays.

Solution: We write

L(x) : x likes fun.

P(x) : x is a play

E(x, y) : x will enjoy y.

Then (∀x) [L(x) → (∀y) (P(y) → E(x, y)] represents the given statement. The statement can also be represented as for each x, if x- likes fun, and for each y, if y is a play, then x enjoys y. So it could be symbolised as

(∀x) (∀y) [L(x) Ʌ P(y) → E(x, y)]