Rules of Inference

Rules of inference

Definition: Inference Theory :

The main function of logic is to provide rules of inference, or principles of reasoning. The theory associated with such rules is known as inference theory because it is concerned with the inferring of a conclusion from certain premises.

Definition: Valid argument or valid conclusion

If a conclusion is derived from a set of premises by using the accepted rules of reasoning, then such a process of derivation is called a deduction or a formal proof and the argument or conclusion is called a valid argument or valid conclusion.

Note: The method of determine whether the conclusion logically follows from the given premises by constructing the relevant truth table is called "truth table technique".

Definition :

Let A and B be two statement formulas. We say that "B logically follows from A" or "B is a valid conclusion (consequence) of the premise A" iff A → B is a tautology, that is A → B.

Just as the definition of implication was extended to include a set of formulas rather than a single formula, we say that from a set of premises {H₁, H₂, … H_m} a conclusion C follows logically if H₁^H₂^...^H_m → C.

(I). Truth table technique :

Given a set of premises and a conclusion, it is possible to determine whether the conclusion logically follows from the given premises by constructive truth tables as follows.

(i) Let P₁, P₂, … P_n be all the atomic variables appearing in the premises H₁, H₂ ... H_m and the conclusion C. If all possible combinations of truth values are assigned to P₁, P₂, … P_n and if the truth values of H₁, H₂ ... H_m and C are entered in a table, then it is easy to see from such a table whether

H₁ ^ H₂ ^ … ^ H_m → C is true.

(ii) We look for the rows in which all H₁, H₂, ... H_m have the value T. If, for every such row, C also has the value T, then H₁ ^ H₂ ^ ... ^ H_m → C holds.

(iii) Alternatively, we may look for the rows in which C has the value F. If, in every such row, atleast one of the values of H₁, H₂, ... H_m is F, then H₁ ^ H₂ ^ … ^ H_m → C also holds.

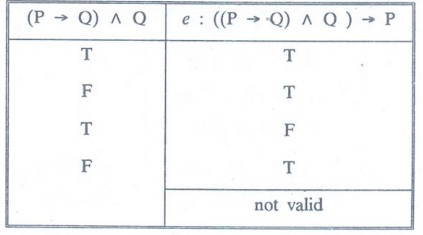
Example: Determine whether the conclusion C follows logically from the premises H₁ and H₂.

(a) H₁ : P → Q     H₂: P       C: Q

(b) H₁ : P → Q     H₂: ┐P     C: Q

(c) H₁: P → Q      H₂: ┐(P^Q)    C: ┐P

(d) H₁: ┐P         H₂: P ↔  Q     C: ┐(P^Q)

(e) H₁: P → Q     H₂: Q       C: P

Solution :

II. Without Using Truth Table

The truth table technique becomes tedious when the number of atomic variables present in all the formulae representing the premises and the conclusion is large. To overcome this disadvantage, we need to investigate other possible methods, without using the truth table.

Now, we discuss the process of derivation by which one demonstrate that a particular formula is a valid consequence of a given set of premises. Before we go to actual process of derivation, we give three rules of inference, which are called Rule P, Rule T and Rule CP respectively.

Before we proceed with the actual process of derivation, we list some important implications and equivalences that will be referred to frequently.

Implications

Equivalences

Example 1.

State which rule of inference is the basis of the following argument:

"It is below freezing now. Therefore, it is either below freezing or raining now".

Solution: Let     P: It is below freezing now

Q: It is raining now

P/PVQ This is an argument that uses the addition rule.

Example 2.

State which rule of inference is the basis of the following argument :

"It is below freezing and raining now. Therefore, it is below freezing now."

Solution: Let P: It is below freezing now.

Q: It is raining now

PɅQ/P This is an argument that uses the simplification rule.

Rules for inferences theory

Rule P: A premise may be introduced at any point in the derivation.

Rule T: A formula S may be introduced in a derivation if S is a tautologically implied by any one or more of the preceding formulas in the derivation,

Rule CP: If we can derive S from R and a set of premises, then we can derive R→S from the set of premises alone.

Note 1: Rule CP is also called the deduction theorem.

Note 2: Whenever the assumed premise is used in the derivation, then the method of derivation is called indirect method of derivation.

Example 3: Demonstrate that R is a valid infernece from the premises P→ Q, Q→R and P.

Solution :

Example 4: Show that R V S follows logically from the premises CVD, (CVD) → ┐H, ┐H → (A^┐B) and (A^┐B) → (RVS).      [MCA M/J 2006]

Solution :

The two tautologies frequently used in the above derivations are I₁₃, known as hypothetical syllogism, and I₁₁, known as modus ponens.

Example 5: Show that S V R is tautologically implied by (P V Q) ^ (P→R) ^ (Q → S)

Solution :

Example 6 : Show that R^ (P v Q) is a valid conclusion from the premises P V Q, Q→ R, P→ M and ┐M.   [A.U. N/D 2007]

Solution :

Example 7: Show I₁₂ : ┐Q, P → Q → ┐P.

Solution :

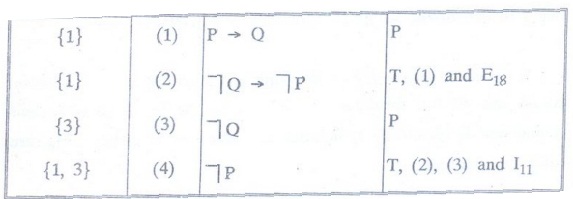
Example 8: Show that R→ S can be derived from the premises P→ (Q→S), ┐R, v P and Q. [A.U. N/D, 2005]

Solution : Instead of deriving R→ S, we shall include R as an additional premise and show S first.

Consistency of Premises and Indirect Method of Proof.

Definition :

A set of formulas H₁, H₂ ... H_m is said to be consistent if their conjunction has the truth value T for some assignment of the truth H_m values to the atomic variables appearing in H₁, H₂, ... H_m .

If for every assignment of the truth values to the atomic variables, atleast one of the formulas H₁, H₂, … H_m is false, so that their conjunction is identically false, then the formulas H₁, H₂, ... H_m are called inconsistent.

In other way, a set of formulas H₁, H₂, ... H_m is inconsistent if their conjunction implies a contradiction, that is

H₁ ^ H₂ ^ … ^ H_m → R^┐R where R is any formula. Note that R^┐R is a contradiction, and it is necessary and sufficient for the implication that H₁^ H₂ ^ … ^ H_m be a contradiction.

Indirect method of proof:

The notion of inconsistency is used in a procedure called proof by contradiction or reduction and absurdum or indirect method of proof.

The technique of indirect method of proof runs as follows :

1. Introduce the negation of the desired conclusion as a new premise.

2. From the new premise, together with the given premises, derive a contradiction.

3. Assert the desired conclusion as a logical inference from the premises.

Example 1: Show that ┐(P ^ Q) follows from ┐P ^ ┐Q.

Solution: We introduce ┐┐(P^Q) as an additional premise and show that this additional premise leads to a contradiction.

Example 2: Show that the following set of premises is inconsistent.

If the contract is valid, then John is liable for penalty. If John is, liable for penalty, he will go bankrupt. If the bank will loan him money, he will not go bankrupt. As a matter of fact, the contract is valid and the bank will loan him money.

Solution: We indicate the given statements as follows :

V: The contract is valid.

L: John is liable for penalty.

M: Bank will loan him money.

B: He will go bankrupt.

Then the given premises are

V → L, L→ B, M → ┐B, V ^ M

Thus the given set of premises leads to a contradiction and hence it is inconsistent.

Example 3 : Show that the following premises are inconsistent.

1. If Jack misses many classes through illness, then he fails high school.

2. If Jack fails high school, then he is uneducated.

3. If Jack reads a lot of books, then he is not uneducated.

4. Jack misses many classes through illness and reads a lot of books. [A.U. A/M, 2004]

Solution :

E: Jack misses many classes.

S: Jack fails high school.

A Jack reads a lot of books.

H: Jack is uneducated.

The premises are E → S, S → H, A → ┐H and E ^ A.

Example 4: Using indirect method of proof, derive P → ┐S from P→ Q V R, Q → ┐P, S → ┐R, P.

Solution: The desired result is P → ┐S. Its negation is P^S.

Since P^S ↔ ┐(┐P v ┐S) ┐(P → ┐S) is a tautology from the law of negation for implication. We include P^S as an additional premise.

Thus additional premise P^S and the given premises together lead to a contradiction. So  (P^S) is derivable from P→ Q, v R, Q → ┐P,S → ┐R, P.

Example 5: Prove by indirect method that (┐Q), P→ Q, PVR ⇒ R

Solution: The desired result is R. Include its negation as a new premise.

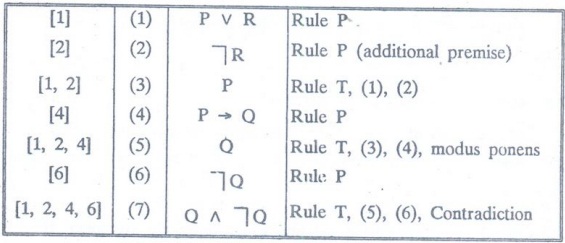
The new premise, together with the given premises, leads to a contradiction. Thus (┐Q), P→ Q, PVR ⇒ R

Example 6: By indirect proof, show that

P→ Q, Q → R, P V R ⇒ R         [A.U. N/D 2004]

Solution: The desired result is R. Include ┐R as a new premise.

Thus we get a contradiction. Therefore we get

P → Q, Q → R, P V R, R.

But, the other premise ┐( P Ʌ R) will not yield a contradiction with R.

Validity of (verbal arguments)

In every day life, we come across argument expressed in (English) sentences. We can represent the pren ses in symbols and verify their validity.

Example 1: Determine the validity of the following argument. If two sides of a triangle are equal, then opposite angles are equal.

Two sides of a triangle are not equal.

Therefore, the opposite angles are not equal.

Solution: Let P: Two sides of a triangle is are equal.

Q: The two opposite angle are equal.

The premises can be represented as

P → Q and ┐P and the conclusion as ┐Q.

If the argument is a valid one then

((P→Q)) ^ ┐P) → ┐Q will be tautology.

Let us now construct the truth table for (P → Q) ^ (┐P) → ┐Q

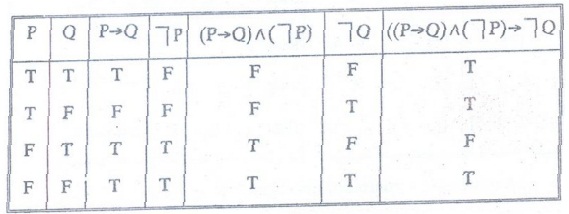
From the truth table we can infer that ((P → Q) ^ (┐P)) → ┐Q is not a tautology.

Hence the argument is not valid.

Example 2: Show the following argument is valid.

"My father praises me only if I can be proud of myself. Either I do well in sports or I ca^ot be proud of myself. If study hard, then I cannot do well in sports. Therefore, if father' praises me, then I do not study well".

Solution: Let

A : My father praises me.

B : I can be proud of myself.

C : I do well in sports.

D : I study hard.

then the given premises are

A → B, C V ┐B, D → ┐C and the conclusion is A→ ┐D.

For, let us assume A as one more premise

Hence it is a valid argument.

Example 3 : Show that the following set of premises is inconsistent.

If the contract is valid, then John is liable for penalty. If John is liable for penalty, he will go bankrupt. If the bank will loan him money, he will not go bankrupt. As a matter of fact, the contract is valid and the bank will loan him money.

Solution: We indicate the given statements as follows:

V: The contract is valid.

L: John is liable for penalty.

M: Bank will loan him money.

B: He will go bankrupt.

Then the given premises are

V→ L, L → B, M → ┐B, V ^ M

Hence it is inconsistent.

Example 4. Show that the following sets of premises are inconsistent. P→ Q, P→R, Q → ┐R, P    [A.U. M/J. 2006]

Solution :

Thus the given set of premises leads to a contradiction and hence it is inconsistent.

Example 5. Show that the following implication by using indirect method. (R→ ┐Q), RVS, S→ ┐Q, P→ Q ⇒ ┐P    [A.U. M/J. 2006]

Solution : To use the indirect method, we will include ┐┐P ↔ P as an additional premise and prove a contradiction.

Example 6. Show that the hypothesis (P^Q) VR and R→S imply the conclusion PVS

Solution :

EXERCISE

1. Derive the following, using rule CP if necessary.

1. ┐P V Q, ┐Q V R, R→S ⇒ P→S

2. P, P → (Q → (R ^ S) ⇒ Q→ S

3. P → Q ⇒ P → (P^Q)

4. (P v Q) → R ⇒ (P^Q) → R

5. P → (Q → R), Q → (R → S) ⇒ P → (Q→S)

2. Show by direct proof:

1. R → (S → Q), ┐P v R and S ⇒ P→ Q

2. If P → Q, R → ┐Q, R then ┐Q.

3. Show by indirect proof:

1. E → S, S → H, A → ┐H → ┐(E^A)

2. If P → (Q^R), (Q v S) → T and (P v S) then T.

4. Show the validity of the following arguments, for which the premises are given in the left and the conclusion on the right.