Ripple/Asynchronous Counters

Ripple / Asynchronous Counters

AU May-03, Dec-09

• A binary ripple/asynchronous counter consists of a series connection of complementing flip-flops, with the output of each flip-flop connected to the clock input of the next higher-order flip-flop.

• The flip-flop holding the least significant bit receives the incoming clock pulses.

• A complementing flip-flops can be obtained from a JK flip-flop with the J and K inputs tied together as shown in the Fig. 5.2.1 or from a T flip-flop.

• A third alternative is to use a D flip-flop with the complement output connected to the D input.

• The D input is always the complement of the present state and the next clock pulse will cause the flip-flop to complement.

• Fig. 5.2.1 (a) shows 2-bit asynchronous counter using JK flip-flops.

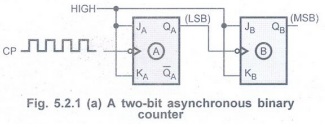
• The clock signal is connected to the clock input of only first stage flip-flop.

• The clock input of the second stage flip-flop is triggered by the Q_A output of the first stage.

• Because of the inherent propagation delay time through a flip-flop, a

transition of the input clock pulse and a transition of the Q_A output of first stage can never occur at exactly the same time. Therefore, the two flip-flops are never simultaneously triggered, which results in asynchronous counter operation.

• Fig. 5.2.1 (b) shows the timing diagram for two-bit asynchronous counter. It illustrates the changes in the state of the flip-flop outputs in response to the clock.

• J and K input of JK flip-flops are tied to logic HIGH hence output will toggle for each negative edge of the clock input.

Example 5.2.1 Extend the counter shown in Fig. 5.2.1 (a) for 3-stages, and draw output waveforms.

Solution:

In Fig. 5.2.2 (b), timing diagram for 3-bit asynchronous counter we have not considered the propagation delays off lip-flops, for simplicity.If we consider the propagation delays of flip-flops we get timing diagram as shown in Fig. 5.2.3.

The timing diagram shows propagation delays. We can see that propagation delay of the first stage is added in the propagation delay of second stage to decide the transition time for third stage. This cumulative delay of an asynchronous counter is a major disadvantage in many applications because it limits the rate at which the counter can be clocked and creates decoding problems.

Example 5.2.2 Draw the logic diagram for 3-stage asynchronous counter with negative edge triggered flip-flops.

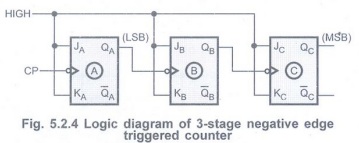
Solution: When flip-flops are negatively edge triggered, the Q output of previous stage is connected to the clock input of the next stage. Fig. 5.2.4 shows 3-stage asynchronous counter with negative edge triggered flip-flops.

Example 5.2.3 A counter has 14 stable states 0000 through 1101. If the input frequency is 50 kHz what will be its output frequency?

Solution :

50 kHz / 14 = 3.57 kHz

Example 5.2.4 The t_pd for each flip-flop is 50 ns, determine the maximum operating frequency for MOD-32 ripple counter.

Solution: We know that MOD-32 uses five flip-flops. With t_pd = 50 ns, the f_max for ripple counter can be given as,

f_max(ripple) = 1/5×50ns = 4 MHz

Example 5.2.5 Draw the logic diagram for 4-stage asynchronous counter with positive edge triggered flip-flops. Also draw necessary timing diagram. Is there any frequency division concept in it?

Solution: When flip-flops are positive edge triggered, the output of previous stage is connected to the clock input of the next stage. Fig. 5.2.5 shows 4-stage asynchronous counter with positive edge triggered flip-flops.

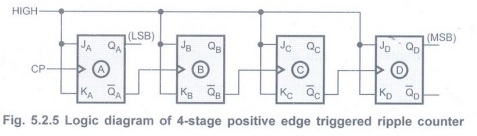
The Fig. 5.2.6 shows the timing diagram for 4-bit ripple up counter using positive edge triggered JK-FFs.

Asynchronous / Ripple Down Counter

• The down counter will count downward from a maximum count to zero.

• The Fig. 5.2.7 shows the 4-bit asynchronous down counter using JK flip-flops.

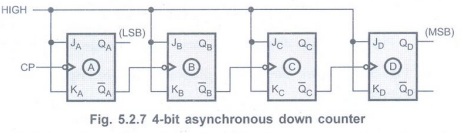
• The clock signal is connected to the clock input of only first flip-flop.

• The clock input of the remaining flip-flops is triggered by the A output of the previous stage instead of Q_A output of the previous stage.

• The Fig. 5.2.8 shows the timing diagram for 4-bit asynchronous down counter. It illustrates the changes in the state of the flip-flop outputs in response to the clock.

• The J and K inputs of JK flip-flops are tied to logic HIGH hence output will toggle for each negative edge of the clock input.

• Down counters are not as widely used as up counters. They are used in situations where it must be known when a desired number of input pulses has occurred. In these situations the down counter is preset to the desired number and then allowed to count down as the pulses are applied. When the counter reaches the zero state it is detected by a logic gate whose output then indicates that the preset number of pulses have occurred.

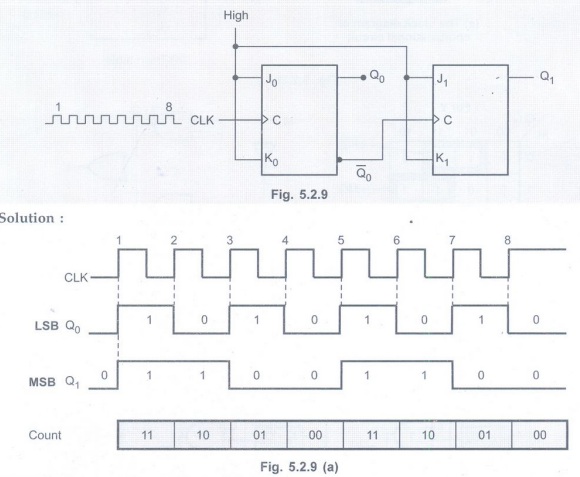
Example 5.2.6 For the ripple counter shown in Fig. 5.2.9, show the complete timing diagram for eight clock pulses, showing the clock, Q₀ and Q₁waveforms.

Asynchronous Up/Down Counter

• To form an asynchronous up/down counter one control input say M is necessary to control the operation of the up/down counter.

• When M = 0, the counter will count down and when M= 1, the counter will count up. To achieve this the M input should be used to control whether the normal flip-flop output (Q) or the inverted flip-flop output () is fed to drive the clock signal of the successive stage flip-flop, as shown in Fig. 5.2.10 (a).

•The truth table is shown in Fig. 5.2.10 (b).

• Fig. 5.2.12 shows the 3-bit up/down counter that will count from 000 up to 111 when the mode control input M is 1 and from 111 down to 000 when mode control input M is 0.

• A logic 1 on M enables AND gates 1 and 2 and disables AND gates 3 and 4. This allows the Q_A and Q_B outputs to drive the clock inputs of their respective next stages. So that counter will count up.

• When M is logic 0, AND gates 1 and 2 are disabled and AND gate 3 and 4 are enabled. This allows the Q_A and Q_B outputs to drive the clock inputs of their respective next stages so that counter will count down.

• Fig. 5.2.13 shows the timing diagram for 3-bit up/down ripple counter.

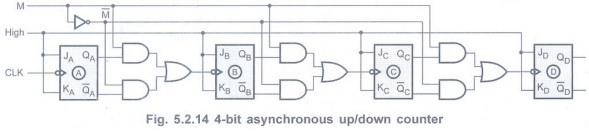
Example 5.2.7 Design a 4-bit up/down ripple counter with a control for up/down counting.

Solution: The 4-bit counter needs four flip-flops. The circuit for 4-bit up/down ripple counter is similar to 3-bit up/down ripple counter except that 4-bit counter has one more flip-flop and its clock driving circuiting.

The Fig. 5.2.14 shows the 4-bit up/down ripple counter.

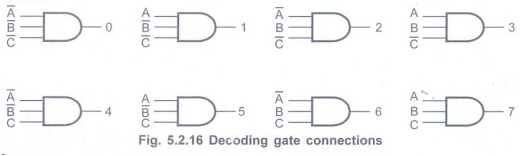
Decoding Gates

• Decoding gates are used to indicate whether counter has reached to particular

state.

• The outputs of the counter are connected to the AND gate as inputs and the output of the AND gate goes high for particular state.

• As shown in Fig. 5.2.15 (a), the output of decoding gate goes high when counter outputs are C = 1, B = 1 and A = 1.

• As shown in Fig. 5.2.15 (b) the output of decoding gate goes high when counter outputs are C = 1, B = 0 and A = 0.

• We can connect corresponding outputs to decoding gate inputs to indicate desired state.

• The Fig. 5.2.16 gives these connections for all possible state detection for 3-bit counter.

Problem Faced by Ripple Counters (Glitch Problem)

• Due to the propagation delay the output flip-flop is delayed by time  tp.

• Fig. 5.2.17 shows the waveform of the circuit which decodes state 7.

• Here, the output of flip-flop A triggers the flip-flop B, hence the B waveform is delayed by one flip-flop delay time (t_p) from the negative transition of A.

• The C waveform is delayed by t_p from each negative transition of B.

• At point X, A goes low (Ā goes high); however, because of flip-flop delay time, B does not go low until point Y. Thus between points X and Y we have the condition C = 1, B = 1 and A = 1. As a result, the output is high between points X and Y. This undesirable output is known as glitch.

• We can avoid the glitch on the output waveform by connecting clock as a fourth input to the decoding gate along with inputs A, B and C. This is illustrated in the Fig. 5.2.17.

Review Questions

1.Explain in detail the operation of a 4-bit binary ripple counter.  AU: Dec.-09, Marks 16

2. Design and explain the working of an up-down ripple counter.  AU: May-03, Marks 8

3. State the problem faced by ripple counters.