Representing Graphs and Graph Isomorphism

Representing Graphs and Graph Isomorphism 

Definition: Matrix representation of graphs and Digraphs:

We can represent a simple graph in the form of edge list or in the form of adjacency lists which are may be useful in computer programming.

Definition: Adjacency matrix

Let G (V, E) be a simple graph with n. Vertices ordered from V₁ to V_n, then the adjacency matrix A = [aij]_n˟n of G is an n˟nsymmetric matrix defined by the elements.

Properties of adjacency matrix

1. An adjacency matrix completely defines a simple graph

2. The adjacency matrix is symmetric

3. Any element of the adjacency matrix is either 0 or 1, therefore it is also called as, bit matrix or boolean matrix.

4. The i^th row in the adjacency matrix is determined by the edges which originate in the node V_i.

5. If the graph G is simple, the degree of the vertex V; equals the number of 1's in the i^th row (or i^th column) of A_G.

6. Given an n˟n symmetric boolean matrix A, we can find a simple graph G s.t A is the adjacency matrix of G.

7. G is null ↔ A(G) is the zero matrix of order n.

Example 1. Use an adjacency list to represent the given graph.

Example 2. Represent the following graph with an adjacency matrix.

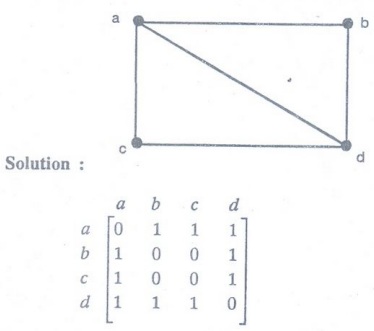
Example 3. Write the adjacency matrix of K₄

Solution: K₄ graph is

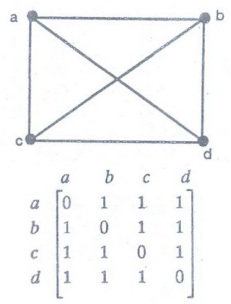
Example 4. Write the adjacency matrix of K_2,3

Solution: K_2,3 graph is

Example 5. Write the adjacency matrix of C₄.

Solution : C₄ graph is

Example 6. Write the adjaency matrix of W₄.

Solution: W₄ graph is

Example 7. Write the adjacency matrix of Q₃

Solution: The Q₃ graph is

Example 8. Draw a graph of the given adjacency matrix.

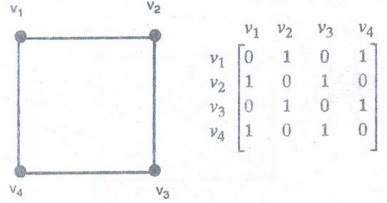
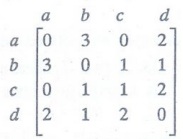
Example 9. Represent the given graph using an adjacency matrix.

Example 10. Find the adjacency matrix of the given directed multigraph.

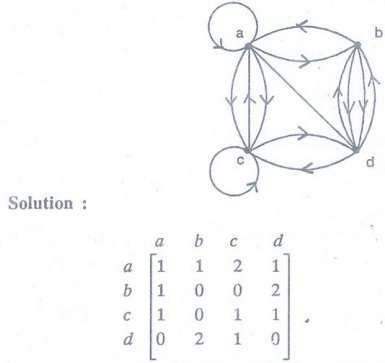
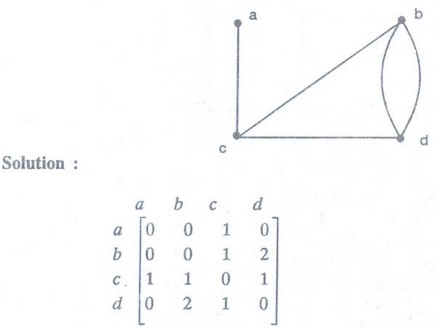
Example 11. Use an adjacency matrix to represent the pseudograph shown in figure.

Solution: The adjacency matrix using the ordering of vertices a, b, c, d is

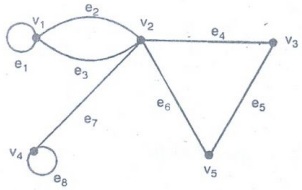
Definition: Incidence matrix

Let G be a graph with n vertices, Let V = {V₁, V₂, ... V_n} and E = (e₁, e₂,...e_m). Define n x m matrix

I_G = [mij]_n˟m where

            

Note :

1. The incidence matrix contains only 0 and 1.

2. The number of 1's in each row equals to the degree of the corresponding vertex.

3. A row with all zeros represents an isolated vertex.

4. Every edge is incident on exactly two vertices, each column of the Incidence matrix has exactly two ones except the loop.

5. The parallel edges in a graph produce idential columns in its incidence matrix.

6. Permutation of any two rows or columns in an incidence matrix simply corresponds to relabeling the vertices and the edges of the same graph.

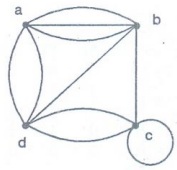
Example 12. Represent pseudograph shown in figure using an incidence matrix.

Solution: The incidence matrix for this graph is

Example 13. What is the sum of the entries in a row of the incidence matrix for an undirected graph?

Solution: Sum is 2 if e is not a loop, 1 if e is a loop.

Example 14. Find the incidence matrices for the graphs (a) K_n    (b) C_n     (c) W_n

Solution:

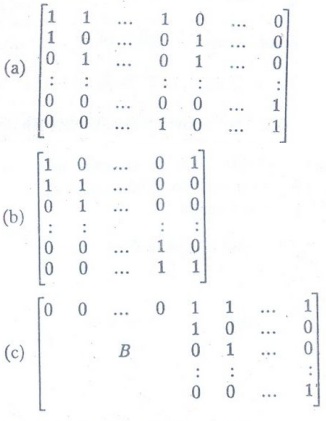
Where B is the answer to (b)

Definition: Isomorphic Graphs

The simple graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂) are isomorphic if there is a one-to-one and onto function f from V₁ to V₂ with the property that a and b are adjacent in G1 if and only if  f(a) and f(b) are adjacent in G₂, for all a and b in V₁. Such a function f is called an isomorphism.

In otherwords

Two graphs G and G' are isomorphic if there is a function f: V (G) → V (G') from the vertices of G to the vertices of G' such that

(i). f is one-to-one

(ii) f is onto and

(iii) For each pair of vertices u and v of G

[u, v] ϵ E (G) ↔ [f(u),ƒ(v)] ϵ E (G')

Any function f with the above three properties is called an isomorphism from G to G'.

Example 15. Explain why the two graphs given below are not isomorphic.

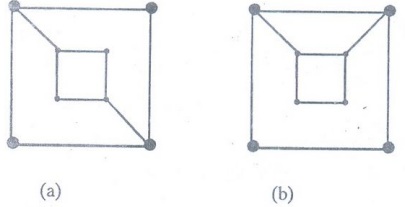
Solution: In the graph (a), no vertices of degree two are adjacent while in the graph (b) vertices of degree two are adjacent. Because isomorphism preserves adjacency of vertices, the graphs are not isomorphic.

Example 16. Show that the graphs G = (V, E) and H = (W, F), shown in figure are isomorphic.

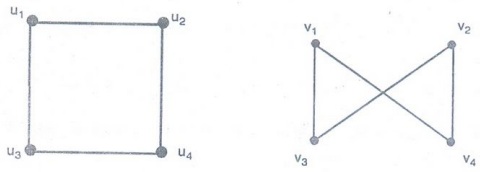
Solution: The function f with f (u₁) = 1, ƒ (u₂) = 4, f (u₃) = 3, and  f(u₄) = 2 is a one-to-one corresponding between V and W.

Here the correspondence preserves adjacency, note that adjacent vertices in G are u₁ and u₂, u₁ and u_з, u₂ and u₄, and u₃ and u₄ and each of the pairs f (u₁) = 1 and f(u₂) = 4. f (u₁) = 1 and f (u₃) = 3, f(u₂) = 4 and ƒ (u₄) = 2, and ƒ (u₃) = 3 and ƒ (u₄) = 2 are adjacent in H.

Example 17. Show that the two graphs shown in figure are isomorphic.

Solution: Here, V(G₁) = {1, 2, 3, 4}, V (G₂) = {a, b, c, d},

E (G₁) = {{1, 2}, {2, 3}, {3, 4}} and E (G₂) = {{a, b}}, {b, d}, {d, c}

Define f: V(G₁) → V (G₂) as

f (1) = a, f(2) = b, f (3) = d and ƒ (4) = c

f is clearly one-one and onto, hence an isomorphism.

{1, 2} ϵ E (G₁) and {f (1), f (2)} = {a, b} ϵ E (G₂)

{2, 3} ϵ E (G₁) and {ƒ(2), f (3)} = {b, d} ϵ E (G₂)

{3, 4} ϵ E (G₁) and {f (3), f (4)} = {d, c} ϵ E (G₂)

{1, 3} € E (G₁) and {f(1), f (3)} = {a, d} € E (G₂)

{1, 4} € E (G₁) and {f(1), f (4)} = {a, c} € E (G₂)

{2, 4} € E (G₁) and {f(2), f (4)} = {b, c} € E (G₂)

Hence ƒ preserves adjacency as well as non-adjacency of the vertices. Therefore G₁ and G₂ are isomorphic.

Example 18. Prove that the graphs G and G given below are isomorphic

Solution: The two graphs have the same number of vertices same number of edges and same degree sequence consider the function f.

f(u₁) V₁, f (u₂) = v₃, f (u₃) = V₄, ƒ (u₄) = V₂, f (u₅) = v₅

then the adjacency matrices of the two graphs corresponding to f are

G and Ğ are isomorphic to each other.

Example 19. Show that the Digraphs are isomorphic.

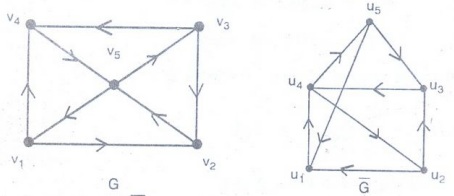
Solution: G and   are having 5 vertices and 8 edges. Consider indegree and out degree of the vertices if G and .

Now

f(v₁) = u₅, f (v₂) = u₁, f (v₃) = u₂

f(v₄)=u₃, f (v₅) = u₄

Clearly f is one to one and onto.

⇒ AG = AĞ  under this mapping f

G and Ğ are isomorphic.

Example 20. Prove that any 2 simple connected graphs with n vertices all of degree 2 are isomorphic.

Solution: We know that total degree of a graph is given by

Σⁿ_i=1 d(V_i)=2|E|

then     |V| = number of vertices n

|E| = number of edges

Further the degree of every vertex is 2.

Therefore        Σⁿ_i=1 2 = 2|E|

2 ((n) − 1 + 1) = 2 |E|

⇒ n = |E|

number of edges = number of vertices. Therefore the graphs are cycle graphs Hence they are isomorphic.

Example 21. Can a simple graph with 7 vertices be isomorphic to its complement?

Solution: A graph with 7 vertices can have a maximum number of edges.

= 7(7-1) / 2 = 7×6 / 2 = 21 = 21 edges

21 edges cannot be split into 2 equal integers. Therefore, G and  cannot equal number of edges. Hence a graph with 7 vertices cannot be isomorphic to its complement.

Example 22. Let G be a simple graph all of whose vertices have degree 3 and |E| = 2 |V| - 3. What can be said about G?

Solution :

Σ^|v|_i=1 d(V_i)=2|E|

3 (|V| - 1+1) = 2|E|

3 |V| = 2 |E|

⇒ 3|V| = 2(2 |V| − 3)

= 3|V| = 4|V| - 6

|V| = 6

Number of vertices in G = 6 It can be concluded that G is isomorphic to K_3,3

Example 23. Show that isomorphism of simple graphs is an equivalence relation.

Solution:

(i) Reflexive: G is isomorphic to itself by the identity function, so isomorphism is reflexive.

(ii) Symmetric: Suppose that G is isomorphic to H. Then there exists a one-to-one correspondence ƒ from G to H that preserves adjacency and nonadjacency. From this f^-1 is a one-to-one correspondence from H to G that preserve adjacency and non adjacency.

Hence, isomorphism is symmetric.

(iii) Transitive: If G is isomorphic to H and H is isomorphic to K, then there are one-to-one correspondences ƒ and g from G to H and from H to K that preserve adjacency and non adjacency. It follows that gof is a one-to-one correspondence from G to K that preserves adjacency and non adjdacency. Hence, isomorphism is transitive.

EXERCISES 3.3

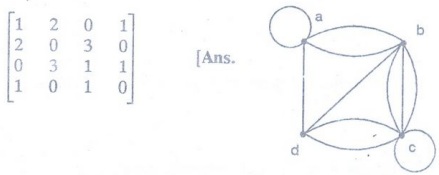
1. Draw a graph with the given adjacency matrix.

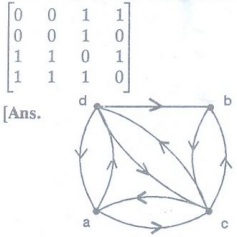
2. Represent the given graph using an adjacency matrix.

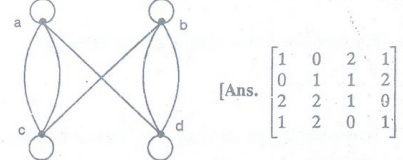
3. Draw an undirected graph represented by the given adjacency matrix.

4. Find the adjacency matrix of the given directed multigraph.

5. Draw the graph represented by the given adjacency matrix.

6. Is every zero-one square matrix that is symmetric and has zeros on the diagonal the adjacency matrix of a simple graph?

[Ans. Yes]

7. Describe the row and column of an adjacency matrix of a graph corresponding to an isolated vertiex.

[Ans. Zeros]

8. Show that the vertices of a bipartite graph with two or more vertices can be ordered so that its adjacency matrix has the form

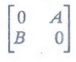
9. Find a self-complementary simple graph with five vertices.

[Ans. C₅]

10. For which integers n is C_n self-complementary?

[Ans. for n = 5 only]

11. How many non isomorphic simple graphs are there with five vertices and three edges ?

[Ans. 4]

12. Are the simple graphs with the following adjacency matrices isomorphic?

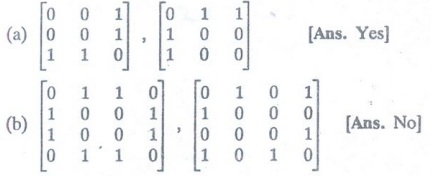
13. Determine whether the given pair of directed graphs are isomorphic.

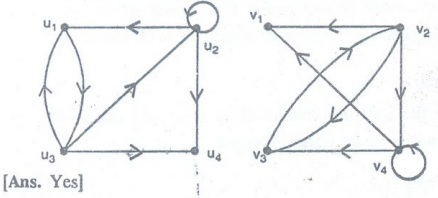
14. Find a pair of non isomorphic graphs with the same degree sequence such that one graph is bipartite, but the other graph is not bipartite.

[Ans. Many answers are possible for example C₆ and C₃UC₃]

15. What is the product of the incidence matrix and its transpose for an undirected graph ?

[Ans. The product is [a_ij] where a_ij is the number of edges from v_i to v_j when i≠j and a_ii is the number of edges incident to v₁ ]