Recurrence Relations

Recurrence Relations

Definition: Recurrence relation : (Sometimes called difference equation).

A recurrence relation for the sequence {a_n} is an equation that shows a_n in terms of one or more of the previous terms of the sequence a₀, a₁, ... a_n-1, for all integers n with n ≥ n₀, where no is a non-negative integer.

Note: A sequence is called a solution of a recurrence relation if its terms satisfy the recurrence relation.

Example: The Fibonancci sequence is defined by the recurrence relation a_r = a_r-2 + a_r-1, r≥ 2, with the initial conditions a₀ = 1 and a₁ = 1.

Example 1: Let {A} be a sequence that satisfies the recurrence relation a_n = a_n-2 + a_n-1 for n = 2, 3, 4, 5, …. and suppose that a₀ = 3 and a₁ = 5. What are a₂ and a₃?

Solution : Given:

a_n = a_n-2 + a_n-1

a₂ = a₀ + a₁ = 3+5 = 8

а_з = a₁+ a₂ = 5 + 8 = 13

Example 2: Find the first five terms of the sequence defined by each of these recurrence relations and initial conditions.

Example 3: Let an 2ⁿ + (5) (3ⁿ) for n = 0, 1, 2, ..

(a) Find a₀, a₁ and a₂. (b) Show that a₄ = 5a₃ - 6a₂.

Solution: (a) Given: a_n = 2ⁿ + (5) (3ⁿ)

a₀ = 2⁰ + (5) (3⁰) = 1 + (5) (1) = 6

a₁ = 2¹ + (5) (3¹) = 2 + (5) (3) = 17

a₂ = 2² + (5) (3²) = 4 + (5) (9) = 49

(b) Given: a_n = 2ⁿ + (5) (3ⁿ)

a₃ = 2³ + (5) (3³) = 8 + 5(27) = 143

To prove: a₄ = 5a₃ – 6a₂ 

L.H.S = a₄ = 2⁴ + (5) (3⁴) = 16 + 5(81) = 421

R.H.S. = 5a₃ - 6a₂

= 5 (143) - 6 (49)

= 715-294

= 421

L.H.S. = R.H.S. Hence the proof.

Example 4: Is the sequence {a} a solution of the recurrence relation a_n = 8 = 8 a_n-1 - 16 a_n-2 if

(a) a_n = 0, YES

⇒a_n-1 = 0

⇒ a_n-2 = 0

a_n = 8 a_n-1 – 16 a_n-2 is true.

(b) a_n = 1, NO

⇒ a_n-1 = 1

⇒ a_n-2 = 1

Example 5: Show that the sequence {a_n} is a solution of the recurrence relation a_n = a_n-1 + 2a_n-2 + 2n - 9 if

(a) a_n = 3(-1)ⁿ + 2ⁿ - n + 2

(b) aⁿ = 7 2ⁿ - n + 2

Solution :

Example 6: (Tower of Hanoi): The tower of Hanoi is a puzzle consisting of three pegs mounted on a board with disks of different diameters. Initially, these disks are placed on the first peg in order of size, with the largest on the bottom (as shown in fig.) These disks are to be transfered on the second peg with their relative positions unchanged. The rules of the puzzle allow disk to be moved one at a time from one peg to another as long as a disk is never placed on the top of smaller one.

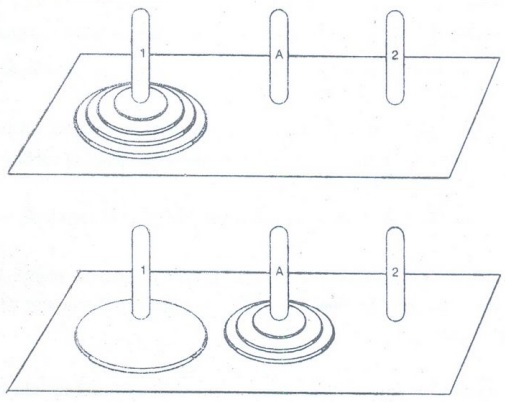
Solution: Let C_n denotes the number of moves needed to solve the n-disk puzzle.

If there is only one disk, simply move it to the second peg.

If we have n > 1, transfer n - 1 disks to peg A using C_n-1 moves.

During the moves, the largest disk at the bottom of peg 1 stays fixed. There we use one move to transfer the largest disk to the second peg.

Now move again n-1 disks on peg A to peg 2 using C_n-1 moves.

C_n = 2 C_n-1 + 1, n > 1 with initial condition C₁ = 1.

Example 7: (Rabbits and the Fibonacci Numbers) A young pair of rabbits (one of each sex) is placed on an island. A pair of rabbits does not breed until they are 2 months old. After they are 2 months old, each pair of rabbits produces another pair each month, as shown in fig. Find a recurrence relation for the number of pairs of rabbits on the island after ʼn months, assuming that no rabbits ever die.

Solution: Let f_n the number of pairs of rabbits after n months.

Show that f_n = n 1, 2, 3, are the terms of the Fibonacci sequence.

The rabbit population can be modeled using a recurrence relation. At the end of the first month, the number of pairs of rabbits on the island is f₁ = 1.

Since this pair does not breed during the second month, f₂ = 1 also.

To find the number of pairs after n months, add the number on the island the previous month, f_n-1, and the number of newborn pairs, which equals f_n-2.

Since each newborn pair comes from a pair atleast 2 months old.

Consequently, the sequence {f_n} satisfies the recurrence relation

f_n = f_n-1 + f_n-2

for n ≥3 together with the initial conditions f_i = 1 and f₂ = 1. Since this recurrence relation and the initial conditions uniquely determine this sequence, the number of pairs of rabbits on the island after n months is given by the nth Fibonacci number.

Example 8 (Compound Interest): A person invests Rs. 10,000/- @ 12% interest compounded annually. How much will be there at the end of 15 years?

Solution: A_n the amount at the end of n years. So at the end of n - 1 years, the amount is A_n-1, because the amount after n years equals the amount after n - 1 years plu interest for the n^th year. Thus the sequence {A_n} satisfies the recurrence relation.

A_n = A_n-1 + (0.12) A_n-1

= (1.12) A_n-1, n ≥1

with initial condition A₀ = 10,000

The recurrence relation with the initial condition allow us to compute the value of A_n for any n.

For example,

A₁ = (1.12) A₀

A₂ = (1.12) A₁ = (1.12)² A₀

A₃ = (1.12) A₂ = (1.12)³ A₀

A_n = (1.12) A₀

which is an explicit formula.

The required amount can be derived from the formula by putting n = 15.

A₁₅ = (1.12)¹⁵ (10000)

Example 9: Find a recurrence relation and give initial conditions for the number of bit strings of length n that do not contain the pattern 11.

Solution: Let C_n denote the number of bit strings of length n that do not contain the pattern 11, and can be counted as

(a) that begin with 0, (b) that begin with 10.

because, the sets of strings of types (a) and (b) are disjoint, by the sum rule, C will be equal to the sum of the numbers of strings of type (a) and (b). Suppose n bit string begins with 0 and does not contain the pattern 11, (n - 1) bit string not containing 11 can follow the initial because 0, there are C_n-1 such bit string of type (a).

In an n bit string begin with 10 and does not contain pattern 11, the (n-2) bit string following the initial 10 can not contain the pattern 11.

There are C-2 bit strings of type (b).

So, C_n = C_n-1 + C_n-2, n ≥ 3

The initial conditions are C₁ = 2, because both bit strings of length 1 and 0 do not contain the pattern 11 and C₂ = 3, because the valid bit string of length two is 00, 01 and 10.

EXERCISE 2.6

1. Find the first five terms of the sequence defined by each of these recurrence relations and initial conditions.

(a) a_n = a²_n-1, a₁ = 2

(b) a_n = na_n-1 + n²a_n-2, a₀ = 1, a₁ = 1.

2. Let a_n = 2ⁿ + 5.3ⁿ for n = 0, 1, 2, ...

(a) Find a₃, and a₄.

(b) Show that a₂ = 5a₁ - 6a₀, a₃ = 5a₂ - 6a₁

(c) Show that a_n = 5a_n-1 - 6а_n-2 for all integers n with n ≥ 2.

3. Show that the sequence {a_n} is a solution of the recurrence relation a_n = -3a_n-1 + 4a_n-2 if

(a) a_n = 0             (b) a_n = 1

(c) a_n = (-4)ⁿ        (d) a_n = 2(-4)ⁿ + 3

4. Is the sequence {a_n} a solution of the recurrence relation

a_n = 8a_n-1 - 16a_n-2 if

(a) a_n = 2ⁿ

(b) a_n = 4ⁿ

(c) a_n = 2.4ⁿ + 3n 4ⁿ

(d) a_n = (-4)ⁿ

(e) a_n = n² 4ⁿ

5. Show that the sequence {a_n} is a solution of the recurrence relation a_n = a_n-1 + 2a_n-2 + 2_n-9 if

(a) a_n = -n + 2     (b) a_n = 5(-1)ⁿ – n+2

6. Find the solution to each of these recurrence relations and initial conditions.

(a) a_n = 3a_n-1,           a₀ = 2

(b) a_n = a_n-1 + 2,       a₀ = 3

(c) a_n = a_n-1 + n,        a₀ = 1

(d) a_n = a_n-1 + 2_n+3         a₀ = 4

7. Suppose that the number of bacteria in a colony triples every hour.

(a) Set up a recurrence relation for the number of bacteria after n hours have elapsed

(b) If 100 bacteria are used to begin a new colony, how many bacteria will be in the colony in 10 hours?

8. A factory makes custom sports cars at an increasing rate. In the first month only one car is made, in the second month two cars are made, and so on, with n cars made in the nth month.

(a) Set up a recurrence relation for the number of cars produced in the first n months by this factory

(b) How many cars are produced in the first year?

9. A vending machine dispensing books of stamps accepts only dollar coins, $1 bills, and $5 bills.

(a) Find a recurrence relation for the number of ways to deposit n dollars in the vending machine, where the order in which the coins and bills are deposited matters.

(b) What are the initial conditions ?

(c) How many ways are there to deposit $10 for a book of stamps ?

10. (a) Find a recurrence relation for the number of bit strings of length n that contain a pair of consecutive 0s.

(b) What are the initial conditions ?

(c) How many bit strings of length seven contain two consecutive 0s ?

11. (a) Find a recurrence relation for the number of ways to climb n stairs if the person climbing the stairs can take one stair or two stairs at a time.

(b) What are the initial conditions?

(c) How many ways can this person climb a flight of eight stairs?

12. (a) Find a recrrence relation for the number of bit strings of length n that do not contain three consecutive 0s.

(b) What are the initial conditions ?

(c) How many bit strings of length seven do not contain three consecutive 0s?

13. (a) Find a recurrence relation for the number of ternary strings that do not contain two consecutive 0s.

(b) What are the initial conditions ?

(c) How manry ternary strings of length six do not contain two consecutive 0s?

14. (a) Find the recurrence relation satisfied by R_n, where R_n is the number of regions that a plane is divided into by n lines, if no two of the lines are parallel and no three of the lines go through the same point.

(b) Find R_n using iteration.

15. How many bit sequences of length seven contain an even number of 0s?

ANSWERS

1. (a) 2, 4, 16, 256, 65, 356, (b) 1, 1, 6, 27, 204

2. 143, 421

4. (a) No, (b) Yes, (c) Yes, (d) No, (e) No