Discrete Mathematics: Unit I: Logic and Proofs
Propositional Equivalences
Logic and Proofs - Discrete Mathematics
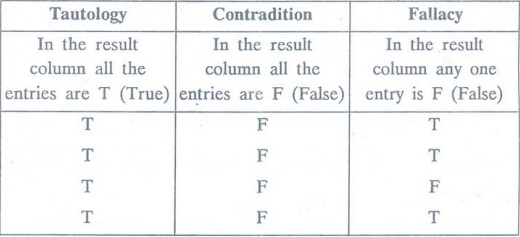
A statement that is true for all possible values of its propositional variables is called a tautology or universely valid formula or a logical truth.
Propositional
Equivalences
Tautology:
A
statement that is true for all possible values of its propositional variables
is called a tautology or universely valid formula or a logical truth.
Contradiction
A
statement that is always false is called a contradiction or absurdity.
Note :
1.
The negation of a contradiction is a Tautology.
2.
A propositional function that is neither a tautology nor a contradiction is
called a contingency.
Example 1:
Show that P V ┐P is a tautology.
Solution
:
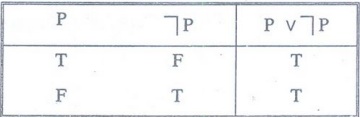
In
the resulting column all the entries are T. Therefore Pv┐P is a tautology.
Example 2:
Show that PP is a contradiction.
Solution
:

In
the resulting column all the entries are F. Therefore PAP is a contradiction.
Example 3 :
Show that Q v (P^┐Q) v (┐p^┐Q) is a tautology. [MCA, M.U 96]
Solution:
Let S = Q v (P^┐Q) v (┐p^┐Q)
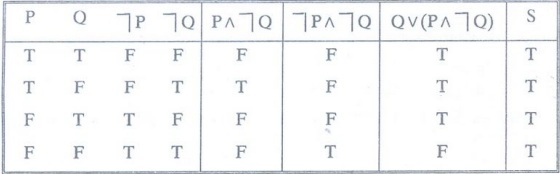
Since
the truth value in the last column is T, the given formula is a tautology.
Example 4:
Using the truth table verify that the proposition
(P^Q)
^ (P v Q) [A.U N/D 2003]
Solution
:
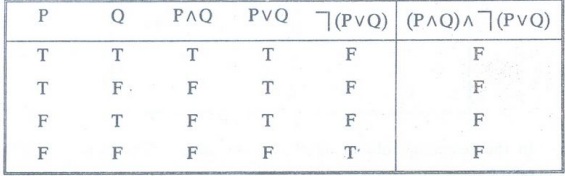
All
the entries in the last column are F therefore the given proposition is a
contradiction.
Example 5:
Show that the proposition (PVQ)<->(QVP) is a tautology.
Solution :

The
last column entries are T. Therefore given formula is a tautology.
Example 6:
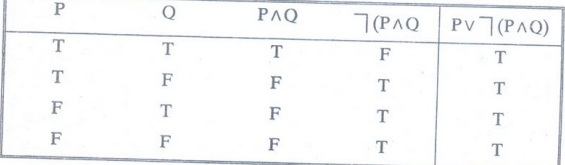
Verify that the proposition PV ┐ (P^ Q) is tautology.
Solution
:
Example 7 :
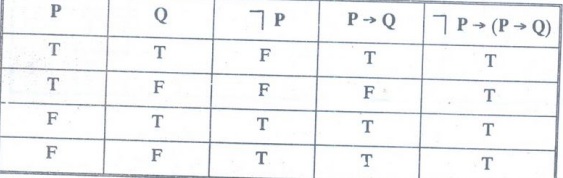
Show that ┐P→ (P→ Q) is a tautology.
Solution :
Example 8:
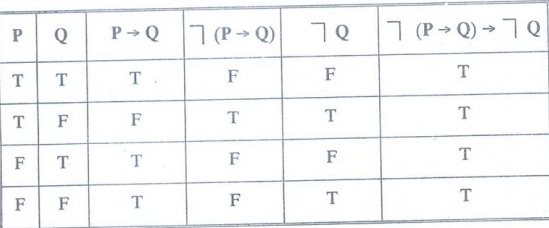
Show that ┐ (P→ Q) → ┐ Q is a tautology
Solution
:
Example 9:
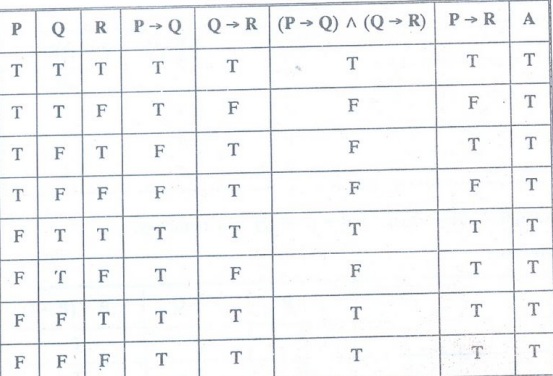
Show that (P→ Q) ^ (Q → R) → (P → R) is a tautology.
Solution:
Let A = (P→ Q)^(Q→ R) → (P → R)
EXERCISE
1.
Prove that each of the following is a tautology.
(a)
(Р^Q) → P
(b)
(P^Q) → Q
(c)
P→ (P VQ)
(d)
Q → (P VQ)
(e)
┐P→ (P->Q)
(f)
┐ (P →Q) → P
(g)
(P ^ (P→ Q)) → Q
(h)
(┐P^ (P v Q)) → Q
(i)
(┐Q^ (P→Q))-> ┐P
(j)
((P->Q) ^ (Q → r)) →(P→ R)
2.
Verify that the proposition (P ^ Q) ^ ┐ (P
v Q) is a contradiction.
3.
Determine the contrapositive of each statement.
(c)
If Raja is a poet, then he is poor.
(b)
Only if Ram studies well he pass the test.
Ans.
(a) If Raja is not poor, then he is not a poet.
(b)
If Ram does not study, then he will not pass the test.
4.
Check if QV (P ^ ┐ Q) v (┐ P ^ ┐ Q) is
tautology.
5.
Verify whether (P v Q) V (PɅ Q) is a contradiction or tautology.
6.
How many rows are needed for the truth table of the formula.
(P
^┐Q) <->((┐RɅS) →T)
7.
What is tautology? Contradiction? [97 M.U]
Discrete Mathematics: Unit I: Logic and Proofs : Tag: : Logic and Proofs - Discrete Mathematics - Propositional Equivalences
Related Topics
Related Subjects
Discrete Mathematics
MA3354 3rd Semester CSE Dept | 2021 Regulation | 3rd Semester CSE Dept 2021 Regulation
