Properties of Lattices - Lattices as Algebraic Systems - Sublattices - Direct Product and Homomorphism Some Special Lattices

Properties of Lattices-Lattices as Algebraic Systems - Sublattices - Direct Product and Homomorphism Some Special Lattices

In order to emphasize the role of an ordering relation, a lattice is first introduced as a partially ordered set. Both lattices and Boolean algebra have important applications in the theory and design of computers. There are many other areas such as engineering and science to which Boolean algebra is applied.

Def. Lattice

A lattice in a partially ordered set (L, ≤) in which every pair of elements a, b Є L has a greatest lower bound and a least upper bound.

Def. Greatest Lower Bound (GLB) and Least Upper Bound (LUB)

Example 1. Let S be any set and P(S) be its power set. The partially ordered set (P(S), ≤) is a lattice in which the meet and join are the same as the operations ∩ and U respectively. In particular, when S has a single element, the corresponding lattice is a chain containing two elements. When S has two and three elements, the diagrams of the corresponding lattices are as shown below.

Example 2.

The set of all natural numbers is a lattice, which respect to the used order relation "less than or equal to".

Example 3. Determine whether the posets represented by each of the Hasse diagrams in figure are lattices.

Solution: The posets represented by the Hasse diagrams in (a) and (c) are both lattices because in each poset every pair of elements has both a least upper bound and a greatest lower bound. On the other hand, the poşet with the Hasse diagram shown in (b) is not a lattice, since the element b and c have no least upper bound.

It is to be noted that each of the elements d, e and ƒ is an upper bound, but none of these three elements precedes the other two with respect to the ordering of this poset.

Example 4. Is the poset (Z⁺, 1) a lattice ?

Solution: Let a and b be two positive integers. The least upper bound and greatest lower bound of these two integers are the least common multiple and the greatest common divisor of these integers, respectively.

It follows that this poset is a lattice.

Example 6. Explain why the partially ordered sets of the following figure are not lattices.

Example 7.

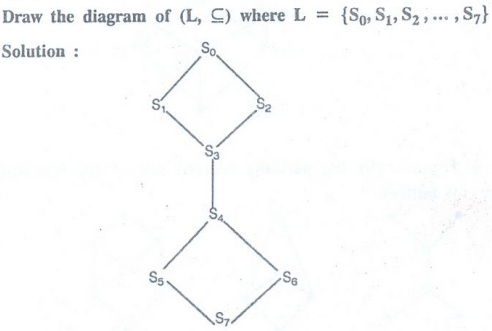
Let the sets S₀, S₁, … , S₇ be given by

S₀ = {a, b, c, d, e, f}

S₁ = {a, b, c, d, e}

S₂ = {a, b, c, d, e , f}

S₃ = {a, b, c, e}

S₄ = {a, b, c}

S₅ = {a, b},

S₆ = {a, c}

S₇ = {a}

Some properties of Lattices

PROPERTY 1: Let (L, ≤) be a lattice. For any a, b, c Є L

PROPERTY 2. Show that the operation of meet are join on a lattice are associative.

Solution: To prove : (a*b) * c = a * (b*c)

Let a, b, c Є L by the definition we have

and

(a*b) *c ≤a*b

(a*b) *c ≤c

By the definition of GLB of a and b, we have a * b ≤ a and a * b ≤b, so by transitive property of ≤ we have

(a*b) *c ≤ a

and   (a*b) *c ≤ b

As   (a*b) c ≤ b and (a*b) * c≤ c

We see that (a*b) * c is lower bound for b and c. From the definition of b*c it follows that (a * b) * c ≤ b*c

As   (a*b) * c ≤ a and (a*b) * c ≤ b * c

From the definition of a * (b*c), we have

(a*b) *c≤ a* (b*c) …. (i)

Now     a* (b*c) ≤ a and a* (b*c) ≤ b *c

As   b*c ≤ b, by tansitivity a * (b*c) ≤ b

since     a* (b*c)≤a , and a * (b* *c) ≤ b

We have a * (b*c) ≤ (a*b)

As    a*(b*c) ≤ b * c ≤ c

a * (b*c) ≤ (a*b) * c …. (ii)

From (i) and (ii), by antisymmetric property, if follows that

a* (b*c) = (a*b) * c

THEOREMS

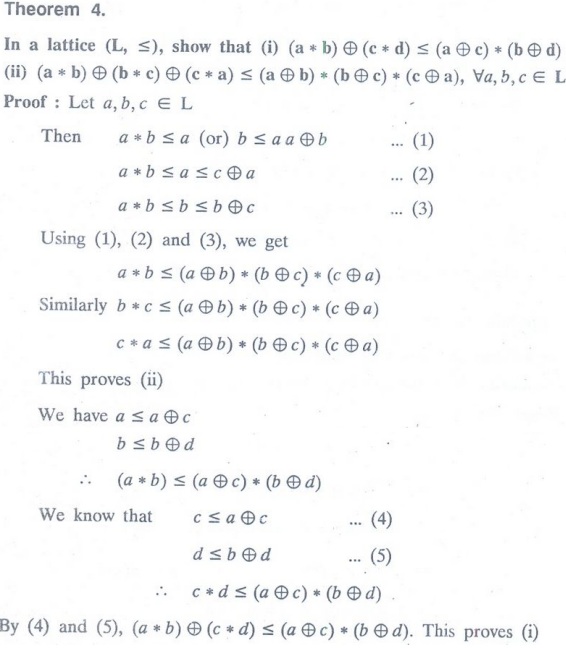
Theorem 7.

Draw Hasse diagram of all lattices with upto five elements.

Solution: The following Hasse diagrams are the lattice with 1, 2, 3, 4 and 5 elements.

Note:

Terminology

Example 1. Let (L, ≤) be a lattice in which L = {a₁, a₂ , ... a₈} and S₁, S₂ and S₃ be the sublattices of L given by S₁= {a₁, a₂, a₄, a₆}, S₂ = {a₃, a₅, a₇, a₈} and S₃ = {a₁, a₂, a₄, a₈}

The diagram of (L, ≤) is

Observe that (S₁, ≤) and (S₂ ≤) are sublattices of (L, ≤), but (S₃, ≤) is not a sublattices because a₂, a₄ Є S₃ but a₂ * a₄ = a₆ Є S₃.

If g: L →L is an isomorphism, then g is called an automorphism.

4. If g: →L is an endomorphism, then the image set of g is a sublattice of L.

Def. Let (P, ≤) and (Q, ≤') be two partially ordered sets.

A mapping f: P → Q is said to be order-preserving relative to the ordering in P and ≤ ' in Q iff for any a, b Є P such that a ≤b, f(a) ≤ 'f(b) in Q.

Note: If (P, ≤) and (Q, ≤ ') are lattices and g: P→Q is a lattice homomorphism, then g is order-preserving.

Def. Two partially ordered sets (P, ≤) and (Q, ≤ ') are called order-isomorphic if there exists a mapping f: P→ Q which is bijective and if both f and f^-1 are order-preserving.

Def. Modular

A lattice (L, ˄, V) is called modular if for all x, y, z Є L, x ≤ z ⇒ x V (y^z) ≥ (xvy) ˄ z (modular equations).

Note: We have (by modular inequality) if x ≤ z  ⇒ x v (y^z) ≤ (xvy) ˄ z holds in any lattice. Therefore to show that a lattice L is modular it is enough to show if,

x ≤ z ⇒ xv (y^z) ≥ (xvy) ˄ z holds in L.

THEOREMS

Theorem 1.

Every chain is a distributive lattice.         [A.U M/J 2013]

Proof :

Let (L, ≤) be a chain

Let a, b, c Є L

Consider the following possible cases.

(i) a ≤ b or a ≤ c and

(ii) a ≥ b and a ≥ c

We shall now show that the distributive law

Theorem 3.

Every distributive lattice is modular.   [A.U. N/D 2004]

Proof :

Let (L, ≤) be a distributive lattice

For all a, b, c Є L, we have

So if a ≤ c, the modular equation is satisfied and L is modular.

Example 1. Show that the Lattices given by the diagrams are not distributive.

Example 2. If D(n) denotes the lattice of all the divisors of the integer n draw the Hasse diagrams of D(10), D(15), D(32) and D(45)

Example 3. Let L be a complemented, distributive lattice. For a, b Є L the following are equivalent.

Example 4. Prove that the following lattice is not modular.

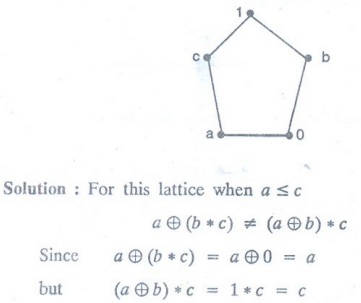
it is not a modular lattice.

Def. Enumeration: A one-to-one correspondence with the elements of a set is called an enumeration.

Example 5. Theorem : State and prove Isotonicity property in a lattice.

Proof: Let (L, ≤) be a lattice. For a, b, c Є L, the following properties called isotonicity laws.

b ≤ c ⇒ a*b ≤ a*c;

(i.e.,) b ≤ c ⇒ a ˄ b ≤ a ˄ c; avb ≤ avc

Let us assume that b ≤ c

(i) Claim: a v b ≤ a v c

Let x = a v c. Then x is lub of a & C

⇒ x is an upper bound of a & c.

a ≤ x, c ≤ x

But b ≤ c, c ≤ x ⇒ b ≤ x

Also a ≤ x

x is upper bound of a & b

But a v b is lub of a & b

a v b ≤  x = a v c

(ii) Claim: a ˄ b ≤ a ˄ c

Let y = a ^ b ⇒ y is glb of a & b

y is a lower bound of a & b

y ≤ a, y ≤ b

Using b ≤ c, y ≤ a, y ≤ c

y is a lower bound of a & c

But a ˄ c is glb of a and c

y ≤ a ˄ c ⇒ a ˄ b ≤ a ˄ c

Example 6. If (L, ˄ , V) is a complemented distributive lattice, then the De Morgan's laws are valid.     [A.U M/J 2013]

Example 7. Let (L, ˄, V) be a distributive lattice and a, b, c Є L If aɅb = aɅc and avb = avc, then b = c           [Cancellation laws are valid in a Distributive lattice]

Proof: Let (L, ˄, V) be any distributive lattice and a, b, c Є L, such that

a ˄ b = a ^ c

and a v b = a v c

Now, (a Ʌ b) V c = (avc) Ʌ (bvc)           (L is distributive]

= (a v b) ^ (b v c)

= (b v a) Ʌ (b v c)

= b v (a ˄ c)

= b v (a ˄b)

= b

and (a ˄ b) v c = (a ^ c) v c = c

Thus b = (a ˄b) v c = c

So that, a ˄ b = a ˄ c

and

a v b = a v c

⇒ b = c

That is, the cancellation law is valid in a distributive lattice.

Example 8 Theorem : A modular lattice is distributive if and only if none of its sublattice is isomorphic to the diamond lattice M₅.

Proof: We have, the diamond lattice M₅ is not distributive lattice, therefore any lattice having sublattice isomorphic to M₅ cannot be distributive.

Conversely, let (L, ≤) be any, modular lattice but not distributive lattice. We show that L has a sublattice isomorphic to M₅. Since (L, ≤) is not distributive lattice, then we an find x, y, z Є L such that

(x^y) V (y^z) V (Z^x) < (xvy) ^ (yvz) ^ (zvx)

Now let,

u = (x^y) v (V^Z) v (z^x)

v = (xvy) ^ (yvz) ^ (zvx)

a = u v (x^v)

b = u v (y^v) and

c = u v (z^v)

Then the elements u, v, a, b, c are distinct and form a sublattice to L, and S {u, a, b, c, v} is isomorphic to the diamond lattice M₅.

Example 9. Show that a chain of three or more elements is not complemented.

Solution: We have, in a chain any two elements are comparable.

Let 0, x, 1 be any three elements in a chain (L, ≤) with least element 0 and greatest element 1.

We have       0 ≤ x ≤ 1

Now,    0^x = 0 and 0vx = x

Similarly,     x^1 = x and xv1 = 1

Therefore, x does not have any compelement.

Hence, any chain with three or more elements is not complemented.

Example 10. Find all sub that of (D₃₀, |), where relation.

Solution: The Hasse diagram of (D₃₀, |) is given by

The sublattices are D₆ = {1, 2, 3, 6}

D₁₀ = {1, 2, 5, 10}

D₁₅ = {1, 3, 5, 15}

S₁ = {5, 10, 15, 30}

S₂ = {3, 6, 15, 30}, etc. are sublattices.

In general, if m❘n then D_m is a sublattice of D_n and D_km is also a sublattice of D_n.

Example 11. Prove that the following lattice is modular.

Solution: The elements a, b and c are symmetric in the lattice. It is enough to prove for any one of a, b, c.

We have the cases a < 1 and 0 < a

Case (i): If a < 1

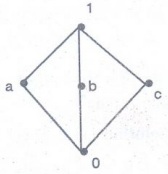
Let x₁ = a and x₃ = 1

Now, x₁ v (x₂^x₃) = (a v (x₂ ^ 1)

= a ν x₂

and (x₁ v x₂) ^ x₃ = (a v x₂) ^ 1

= q v x₂

Hence x₁ v (x₂ ^ x₃) = (x₁ v x₂) ^ x₃

Case (ii) if 0 < a.

Let x₁ = 0 and x₃ = a

Now x₁ v (x₂ ^ x₃) = 0 v (x₂ ^ a)

= x₂ ^ a

(x₁ v x₂) ^ x₃ = (0 v x₂) ^ a

= x₂ ^ a

x₁ v (x₂ ^ x₃) = (x₁ ^ x₂) ^ x₃

Hence the above lattice is modular.

Example 12. Show that the direct product of any two distributive lattices is a distributive lattice.

Solution :

Let L₁ and L₂ be two distributive lattices. Let x, y, z Є L₁˟ L₂, the direct product (lattice) of L₁ and L₂. Then x = (a₁, a₂), y = (b₁, b₂), and z  = (c₁, c₂), for some a₁, b₁, c₁ Є L₁ and a₂, b₂, c₂ Є L₂

Now x v (y ^ z)

= (a₁, a₂) v ((b₁, b₂) ^ (c₁, c₂)

= (a₁, a₂) v (b₁ ^ c₁, b₂^c₂)

= (a₁ v (b₁^c₁), a₂ v (b₂ ^ c₂))

= ((a₁ vb₁) ^ (a₁ v c₁), (a₂ v b₂) ^ (a₂ v c₂)) as L1 and L2 are distributive.

= ((a₁ v b₁), (a₂ v b₂)) ^ ((a₁ v c₁), (a₂ v c₂))

= ((a₁, a₂) v (b₁, b₂)) ^ ((a₁, a₂) v (c₁, c₂))

= (x v y) ^ (x v z)

So for all x, y, z Є L₁ ˟ L₂, x v (y ^ z) = (x v z) ^ (x v z)

Thus if L₁ and L₂ are distributive, then L₁ ^ L₂ is also distributive.

Example 13. In a distributive lattice, complement of an element is unique.

Proof :

Let a be an element with two distinct complement b and c. Then

a * b= 0 and a * c = 0

⇒ a * b = a * c

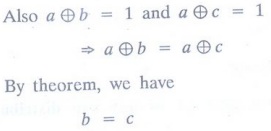
Example 14. State and prove the necessary and sufficient condition for a lattice to be modular.

(OR)

A lattice L is modular if and only if none of its sublattices is isomorphic to the pentagon lattice N₅.

Proof : Since the pentagon lattice N₅ is not modular lattice. Hence any lattice having a pentagon as a sublattice cannot be modular.

Conversely, let (L, ≤) be any nonmodular lattice we shall prove there is a sublattice which is isomorphic to N₅.

As (L, ≤) is a nonmodular lattice, then there are elements a, b, c Є L such that

a ≤ c and a v (b^c) ≠ (avb) ^ c

Let u = b^c

x = a v (b^c)

y = b

z = (a v b) ^ c

v = avb

Then all the elements u, x, y, z, v are distinct, we have u ≤ x ≤ z ≤ v and u ≤ y ≤ v

(i) u ≤ x^y ≤ z^y = (avb) ^ c ^ b

= ((avb) ^ b) ^ c

= b^c = u

Therefore x^у = z^y = u

(ii) v ≥ zvy ≥ xvy = (a v (b^c)) v b

= a v ((b^c) v b)

= avb = v

So that, xvy = zvy = v

The above observation of S = {u, x, y, z, v} can be represented by a Hasse diagram given by

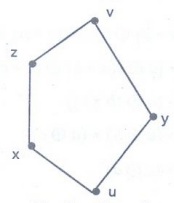
Therefore, the sublattice S = {u, x, y, z, v} of (L, ≤) is isomorphic to N₅.

Thus, we proved that if (L, ≤) is not modular, then it has a sublattice isomorphic to N₅.

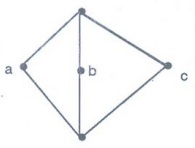
Example 15. Give an example of a lattice which is a modular but not a distributive.          [A.U. A/M 2005]  [A.U. M/J 2006]

Solution: M₅ → diamond lattice

In M₅, a v (b^c) = av0 = a while (avb) ^ (avc) = |^| =1

So M₅ is not distributive.

As N₅ is not a sublattice of M₅, M₅ is modular.

Example 16. Theorem: In a distributive lattice, show that

Example 17. Show that Every distributive lattice is modular. Whether the converse is true? Justify your claim.        [A.U. N/D 2004, M/J 2006]]

Solution :

Proof :

Let (L, ≤) be a distributive lattice

For all a, b, c Є L, we have

So if a ≤ c, the modular equation is satisfied and L is modular.

However, the converse is not true,

Example of lattice which is modular but not a distributive.

M₅ → diamond lattice

In M₅, a v (b^c) = av0 = a while (a v b) ^ (a v c) = |^| = 1

So M₅ is not distributive.

As N₅ is not a sublattice of M₅, M₅ is modular.       

Example 18. In S₄₂ is the set all divisors of 42 and D is the relation "divisor of" on S₄₂, prove that {S₄₂, D} is a complemented lattice.   [A.U N/D 2010 R-2008]

Solution: D₄₂ = {1, 2, 3, 6, 7, 14, 21, 42}

The Hasse diagram of D₄₂ is given in figure.

The zero element of the lattice is 1 and the unit element of the lattice is 42.

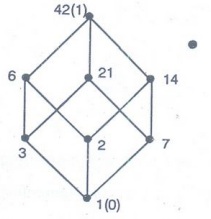
1 V 42 = LCM {1, 42} = 42 = '1'

and 1 ˄ 42 = GCD {1, 42} = 1 = '0'

1' = 42

Similarly we can find that

2' = 21, 3' = 14, 6' = 7, 7' = 6, 14' = 3, 21' = 2 and 42' = 1

Since every element of D42 has a complements, it is a complemented lattice.

Example 19. Check whether the posets {(1, 3, 6, 9), D} and {(1, 5, 25, 125), D} are lattices or not. Justify your claim.              [A.U A/M 2011 R-2008]

Solution :

The poset {(1, 3, 6, 9), D} is not a lattice, since lub (6, 9) and lub (9, 12) does not belong to the poset.

The poset {(1, 5, 25, 125), D} is a lattice as if is a totally ordered set.

Example 20. Does the following lattice a complemented lattice?     [A.U June 2011 R-08]

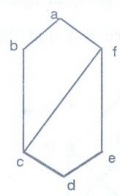
The elements C and ƒ do not have complement.

The given lattice is not a complemented lattice.

Example 21. Given an example of a distributive lattice but not complemented.

  [A.U M/J 2013 R-08/10]

Solution :

No complements exist for 0, b, c, d, 1

The element 'a' is a complement of d and vice versa.

The above graph is not complemented.

Example 22. Draw the Hasse diagram of <X, < >, where X = {2, 4, 5, 10, 12, 20, 25} and the relation ≤ be such that x ≤ y if x divides y. [A.U N/D 2013 R-08/10]

Solution :

(2, 4), (2, 10), (2, 12), (2, 20)

(4, 12), (4, 20),

(5, 10), (5, 20), (5, 25)

(10, 20)

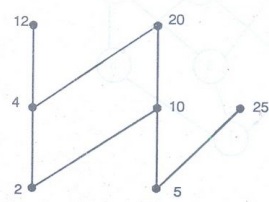
Example 23. Let D₃₀= {1,2,3,5,6,10,15,30} and let the relation R be divisor on D₃₀

(1) all the lower bounds of 10 and 15

(2) the glb of 10 and 15

(3) all upper bound of 10 and 15

(4) the lub of 10 and 15

(5) draw the Hasse diagram.        [A.U N/D 2015 R-13]

Solution :

Given: D₃₀ = {1, 2, 3, 5, 6, 10, 15, 30}

(1) all the lower bounds of 10 and 15 are 5, 1

(2) the glb of 10 and 15 is 1.

(3) all upper bound of 10 and 15 are 30

(4) the lub of 10 and 15 is 30

(5) draw the Hasse diagram is

Example 24. Examine whether the lattice given in the following Hasse diagram is distributive or not.

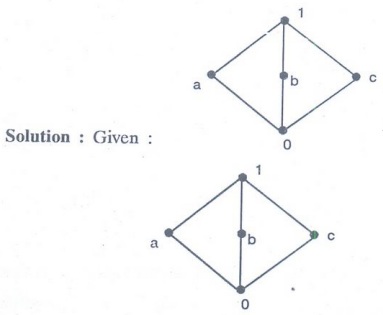
a v (b ^ c) = a v 0 = a

(a v b) ^ (a v c) = 1^1 = 1

a v (b ^ c) ≠ (a v b) v (a v c)

It is not distributive.

Example 25. Consider the set D₅₀ = {1, 2, 5, 10, 25, 50} and the relation divides () be a partial ordering relation on D₅₀

(1) Draw the Hasse diagram of D₅₀ with relation divides.

(2) Determine all upper bounds of 5 and 10.

(3) Determine all lower bounds of 5 and 10.

(4) Determine LUB of 5 and 10.

(5) Determine GLB of 5 and 10.

Solution :

Upper bounds of (5, 10)

Since 5/10, 10/10, 10 is an upper bound of (5, 10)

Since 5/50, 10/50, 50 is an upper bound of (5, 10)

10, 50 are the upper bounds of (5, 10)

Lower bounds of (5, 10)

Since 1/5, 1/10, 1 is a lower bound of (5, 10)

Since 5/5, 5/10, 5 is a lower bound of (5, 10)

1, 5 are the lower bounds of (5, 10)

LUB of (5, 10) is 10

GLB of (5, 10) is 5.

Example 26. Let D₁₀₀ = {1, 2, 4, 5, 10, 20, 25, 50, 100} be the divisions of 100. Draw the Hasse diagram of (D₁₀₀, l) where l is the relation "division".

Find (1) glb {10, 20} (II) lub {10, 20} (III) glb {5, 10, 20, 25} (IV) lub {5, 10, 20, 25}     [A.U N/D 2019 R-17]

Solution :

D₁₀₀ = {1, 2, 4, 5, 10, 20, 25, 50, 100}

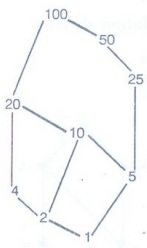
GLB {10, 20} = 10

LUB {10, 20} = 20

GLB {5, 10, 20, 25} = 5

LUB {5, 10, 20, 25} = 100

EXERCISE 5.2

1. Find the complements of every element of the lattice (S_n, D) for n = 75.

2. Show that in a lattice with two or more elements, no element is its own complement.

3. Which of the two lattices (S_n, 3) for n =30 and n = 45 are complemented? Are these lattices distributive ?

4. Show that in a bounded lattice, the elements which have complements from a sublattice.

5. Show that in a distributive lattice, the distributive laws can be generalized as

6. Show that every interval of a lattice is a sublattice.

7. Find all the sublattices of the lattice (S_n, D) for n = 12

8. Show that the lattice (S_n, D) for n = 216 is isomorphic to the direct product of lattices for n = 8 and n = 27.

9. Show that a lattice with three or fewer elements is a chain.

10. Prove that every finite subset of a lattice has an LUB and a GLB.