Permutation and Combinations

Permutation and Combinations

Permutation

A permutation of a set of distinct objects is an ordered arrangement of these objects.

Note: Permutation means selection and arrangement of factors.

Notation: n P_r, (or) P (n, r) (or) P_n,r (or) P_n^r (or) (n)_r

r - Permutation

An r permutation of n (distinct) elements x₁, x₂, ... x_n is an ordering of an r-element subset {x₁, x₂, …x_n}. The number of r-permutations of a set of n distinct elements is denoted by P (n, r).

Example :

2-permutations of {x, y, z} are xy, yx, zx, xz, yz, zy, there are six 2-permutations of this set with three elements, note that there are three ways to choose the first element of the arrangement and two ways to choose the second element of the arrangement. By the product rule, it follows that P (3, 2) = (3) (2) = 6.

Note: The product rule to find a formula for P (n,r) whenever n and r are positive integers with 1 ≤ r ≤ n.

Theorem: If n is a positive integer and r is an integer with 1≤r≤ n, then there are P (n, r) = n (n - 1) (n − 2)... (n - r + 1) r - permutations of a set with n distinct elements.

Proof: We apply the product rule to prove that this formula is correct.

The first element of the permutation can be chosen in 'n' ways since there are n elements in the set.

The second element of the permutation can be chosen in n-1 ways since there are n-1 elements left in the set after using the element picked for the first position.

Similarly, there are n- 2 ways to choose the third element, and so on, until there are exactly n-(r-1) = n-r+1 ways to choose the r^th element.

By the product rule

nP₁ = n

nP₂ = n (n - 1)

nP₃ = n (n − 1) (n − 2)

…………………

…………………

nP_r = n (n - 1) (n − 2) … (n - (r-1)

(i.e.,) nP_r = n (n - 1) (n - 2) ... (n − r + 1)

= n! / (n − r)!

Results:

1. P (n, n) = n!

2. P (n, r) = 0 if r > n

3. P (n, 0) = 1 whenever n is a non negative integer since there is exactly one way to order zero elements.

Corollary 1: If n and r are integers with 0 ≤ r ≤ n, then

P (n, r) = n! / (n − r)!

Proof: We know that P (n, r) = n! / (n − r)!

If r = 0, P (n, 0) = n! / (n-0)! = n! / n! = 1

whenever n is a non-negative integer.

We see that the formula P (n, r) = n! / (n-r)!  also true.

when r = 0

Corollary 2:

The number of permutations of n things taken all at a time is n!

Proof : We know that P (n, r) = n! / (n − r)!

Here r = n,    P (n, n) = n! / (n-n)! = n! / 0! = n!

Note:

1. The number of "r-sequence" of n objects (with repetition) is n^r.

2. Let P (n: n₁, n₂, .. n_r) denote the number of permutations of n objects of which n₁ are alike, n₂ are alike, … n_r are alike,

P (n: n₁, n₂, ... n_r) = n! / n₁! n₂! …. n_r!

3. The number of ways in which n distinct objects can be arranged in a cycle without repetition is (n - 1)!.

Combinations

A combination is a selection of objects without regard to order.

(or) A combination is an unordered collection of distinct objects.

Example: abc is the combination of three objects a, b and c.

Note:

1. The number of r-combinations of n distinct objects is denoted by n C_r (or) C_{(n, r)} (or) (ⁿ_r)

2. nC_n = nC₀ = 1

3. nc_r = nC_n-r (or) C(n, n-r) = C(n, r)

4. C(n, r) = P(n, r) / r!

Theorem: The number of r- combinations of a set with n elements, where n is a non-negative integer and r is an integer with 0 ≤r≤ n, equals

C (n, r) = n! / r! (n-r)!

Proof: The r-permutations of the set can be obtained by first forming the C (n, r) r - combinations of the set and then arranging (ordering) the elements in each r-combination, which can be done in P (r, r) ways.

Thus,   P(n, r) = C(n, r) P(r, r)

Example 1: Find the value of these quantities (a) P (6, 3), (b) P (8, 1), (c) P (8, 8), (d) C (5, 3), (d) C (8, 0).

Example 2: Determine the value of n if (4) (n P₃) = (n + 1) P₃

Solution: Given: (4) (n P₃) = (n + 1) P₃

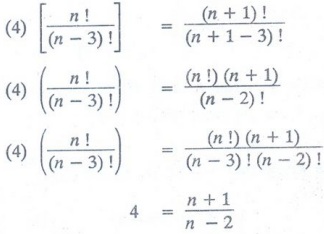
4 (n-2) = n + 1

4n-8 = n + 1

3n = 9

n = 3

Example 3 Determine the value of n if 20 C_n+2 = 20 C_2n-1

Solution: Given: 20 C_n+2 = 20 C_2n-1

Formula n C_x = nC_y ⇒ n = x + y or x = y

n+2 = 2n-1

3 = n

(i.e.,) n = 3

Example 44: How many permutations of {a, b, c, d, e, f, g}. (i) end with a?, (ii) begin with c, (iii) begin with c and end with a, (iv) c and a occupy the end places.

Solution

(i) The last position can be filled in only one way.

The remaining 6 letters can be arranged in 6! ways.

The total number of permutations ending with a are = (6!) (1) = 720

(ii) The first position can be filled in only one way.

The remaining 6 letters can be arranged in 6! ways.

The total number of permutations starting with 'c' are = 1 × 6! = 720

(iii) The first position can be filled in only one way and the last position can be filled in only one way.

The remaining 5 letters can be arranged in 5! ways.

The total number of permutations begin with c and with a is

= (1) (5!) (1) = 5! = 120

(iv) 'c' and 'a' occupy end positions in 2! ways and the remaining 5 letters can be arranged in 5! ways.

Total number of permutations= (5!) (2!) = (120) (2)

= 240

Example 5: How many permutations of the letters A B C D E F G contain (a) the string BCD, (b) the string CFGA, (c) the strings BA and GF, (d) the strings ABC and DE, (e) the strings ABC and CDE?

Solution :

(a) Taking BCD as one object, we have the following 5 objects : A, (BCD), E, F, G

These 5 objects can be permuted in

P (5, 5) 5! = 120 ways.

(b) CFGA as one object, we have the following 4 objects, B, D, E, (CFGA).

The number of ways of permuting these 4 objects = 4! = 24 ways

(c) The objects (BA), C, D, E and (GF) can be permuted in 5! = 120 ways.

(d) The objects (ABC), (DE), F, G can be perrmuted in 4! = 24 ways.

(e) Eventhough (ABC) and (CDE) are two strings, they contain the common letter C.

If we include the strings (ABCDE) in the permutations, it includes both the strings (ABC) and (CDE) We cannot use the letter C twice.

Hence, we have to permute the 3 objects (ABCDE), F and G. This can be done in 3! = 6 ways.

Example 6: How many bit strings of length 10 contain (a) exactly four 1's, (b) atmost four 1's, (c) atleast four '1s (d) an equal number of 0's and 1's ?

Solution :

(a) A bit string of length 10 can be considered to have 10 positions, should be filled with four 1's and six 0's.

Number of required bit strings = 10! /4!6! = 210

Example 7: How many possibilities are there for the win, place and show (first, second and third) positions in a horse race with 12 horses if all orders of finish are possible ?

Solution: The number of ways to pick the three winners is the number of ordered selections of three elements from 12,

(i.e.,) P (12, 3) = (12) (11) (10) = 1320

Example 8 Find the number of 5-permutations of a set with nine elements.

Solution: The given is nothing but P (9, 5) = 9 P₅ = 15120.

Example 9 Suppose that there are eight runners in a race. The winner receives first prize, the second-place finisher receives second prize, and the third place finisher receives third prize. How many different ways are there to receive these prizes, if all possible outcomes of the race can occur and there are no ties?

Solution: The number of ways to pick the three prize winners in the number of ordered selections of three elements from 8.

P (8, 3) = (8) (7) (6) = 336 possible ways.

Example 10: In how many ways can a set of five letters to be selected from the English alphabet ?

Solution: The number ways to pick five letters from 26 is

= 26C₅ = 65,780.

Example 11: How many bit strings of length n contain exactly r 1s?

Solution: The positions of r 1s in a b it string of length n form an r-combination of the set {1, 2, 3, ... n}.

Hence, there are C (n, r) bit strings of length n that contain exactly r 1s.

Example 12: Suppose that there are 9 faculty members in the mathematics department and 11 in the computer science department. How many ways are there to select a committee to develop a discrete mathematics course at a school if the committee is to consist of three faculty members from the mathematics department and four from the computer science department ? [A.U N/D 2012]

Solution: By the product rule, the answer is the product of the number of 3-combinations of a set with nine elements and the number of 4 combinations of a set with 11 elements. By theorem, the number of ways to select the committee is

C (9, 3). C (11, 4) = 9!/3!6! . 11!/4!7! = (84) (330) = 27,720.

EXERCISE 2.5

1. How many subsets with more than two elements does a set with 100 elements have?

2. List all the permutations of {a, b, c}.

3. A coin is flipped 10 times where each flip comes up either heads or tails. How many possible outcomes ?

(a) are there in total ?

(b) contain exactly two heads?

(c) contain the same number of heads and tails ?

4. How many ways are there for eight men and five women to stand in a line so that no two women stand next to each other? [Hint: First position the men and then consider possible positions for the women.]

5. The English alphabet contains 21 consonants and five vowels. How many strings of six lowercase letters of the English alphabet contain?

(a) exactly one vowel ? (c) atleast one vowel ?

(b) exactly two vowels? (d) atleast two vowels ?

6. How many 4-permutations of the positive integers not exceeding 100 contain three consecutive integers k, k + 1, k + 2 in the correct order?

(a) where these consecutive integers can perhaps be separated by other integers in the permutation ?

(b) where they are in consecutive positions in the permutation?

7. How many bit strings contain exactly eight Os and 10 1s if every 0 must be immediately followed by a 1?

8. How many license plates consisting of three letters followed by three digits contain no letter or digit twice?

 9. How many bit strings of length 10 contain atleast three 1s and atleast three Os ?

10. How many ways are there for a horse race with three horses to finish if ties are possible? (Note: Two or three horses may tie).

ANSWERS

1. 2¹⁰⁰ - 5051

2. abc, acb, bac, bca, cab, cba

3. (a) 1024, (b) 45, (c) 252

4. 609, 638, 400

5. (a) 122,523,030, (b) 72,930,375, (c) 223,149,655, (d) 100,626,625

6. (a) 37927, (b) 18915

7. 45

8. 11,232,000

9. 912

10. 13