Particle in a Three Dimensional Potential Box

PARTICLE IN A THREE DIMENSIONAL POTENTIAL BOX

The solution of one-dimensional potential box can be extended for a three dimensional potential box. In a three dimensional potential box, the particle (electron) can move in any direction in space. Therefore instead of one quantum number 'n', we have to use three quantum number n_x, n_y and n_z corresponding the three co-ordinate axis (ie) x, y and z respectively.

Particle in a three dimensional potential box

Let us consider a particle enclosed in a 3-dimensional potential box of length a, b and c along x, y and z axis respectively as shown in fig 1.7.

Since the particle inside the rectangular box has elastic collisions with the walls, the potential energy of the electron inside the box is constant and can be taken as zero for simplicity.

We can say that outside the box and on the wall of the box, the potential energy is ∞.

The boundary conditions are

To find the wavefunction of the particle within the boundary conditions (1). Let us consider the 3-dimensional schrodinger time independent wave equation,

i.e.,

............(3)

Since V=0 [For a free particle], we can write eqn (3) as

............(4)

Equation (4) is a partial differential equation, in which Ψ is a function of

three variables, x, y and z.

We can solve this using method of separation of variables.

The solution for eqn (4) can be written as

Ψ (x, y, z) = X (x) Y (y) Z (z)

Which means Ψ is  a function of x, y and z and is equal to product of 3 functions i.e., X, Y and Z.

Where X is a function of x only

Y is a function of y only

and Z is a function of z only

We can write the solution for equation (4) as

 Ψ = XYZ ….(5)

Differentiating eqn (5), Partially with respect to 'x', twice, we get

............(6)

Similarly differentiating eqn (5) partially with respect to 'y', twice, we get

............(7)

Similarly differentiating eqn (5) partially with respect to 'z', twice, we get

............(8)

Substituting equations (5), (6), (7) and (8) in eqn (4) we get

Dividing by XYZ on both sides we get

............(9)

(or)............(10)

where............(11)

In equation (10), L.H.S. is independent of each other and is equal to a constant in R.H.S. we can equate each term of L.H.S. to each constant in R.H.S.

We can write

or)............(12)

(or)............(13)

(or)............(14)

Equations (12), (13) and (14) represents the differential equations in

x, y and z co-ordinates. The solution for equation (12) can be written as

X (x) = A_x sink_x x + B_x cos k_x x ....(15)

where A and B, are arbitrary constants, which can be found by applying boundary conditions.

i.e., (i) When x=0; X=0

Equation (15) becomes

0=0+Bx

B_x=0 .....(16)

(ii) When x = a; X=0

Equation (15) becomes

0 = A_x sink_x a

Here A_x ≠ 0

[Because, if A_x = 0, then X (x) becomes zero, which implies that the particle. is not there, and is meaningless]

sin k_x a = 0

We know sin n_x π = 0

Comparing the above two equations we can write k_x a = n_x π

(or)............(17)

Substituting equations (16) & (17) in eqn (15) we get

............(18)

Equation (18) represents the un-normalized wave function

Normalization

Eqn (18) can be normalized by integrating it within the limits i.e., boundary conditions 0 to a,

(or)............(19)

Substituting eqn (19) in (18) we get

............(20)

Similarly by solving equation (13) and equation (14) with the boundary conditions 0 to b and 0 to c respectively, we can write

............(21)

............(22)

Eigen functions

The complete wave function, for equation (4) can be written as

Ψ (x, y, z) = X (x) Y (y) Z (z)

Substituting equations (20), (21) and (22) in the above equation, we get

............(23)

Equation (23) represents the eigen function for an electron in a rectangular box.

Eigen values

From equation (11) we can write

............(24)

From equation (17) we can write

similary we can write

Substituting these values in eqn (24), we get

(or)............(25)

Equation (25) represents the energy eigen values of an electron in a rectangular box.

Cubical box

For a cubical box, a = b = c,

We can write equation (25) as

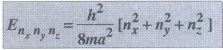............(26)

The corresponding normalized wave function of an electron in a cubical box can be obtained from equation (23), as

From equations ……(26) and ….(27) we can note that, several combinations of the three quantum numbers (n_x, n_y, and n_z) leads to different energy eigen values and eigen functions.

Example

If a state has quantum numbers n_x = 1; n_y = 1; n_z =2

Then, n_x²+n_y²+n_z² = 6

Similarly for n_x = 1; n_y = 2; n_z = 1 combination and n_x = 2; n_y = 1; n_z = 1 combination we have n_x²+n_y²+n_z² = 6

............(28)

The corresponding wave functions can be written as

............(29)