Partial ordering - Posets - Lattices as Posets

UNIT V: LATTICES AND BOOLEAN ALGEBRA

SYLLABUS

Partial ordering – Posets - Lattices as Posets – Properties of Lattices Lattices as Algebraic systems - Sub lattices - direct product and Homomorphism - Some Special lattices - Boolean Algebra.

PARTIAL ORDERING-POSETS-LATTICES AS POSETS

Def. Partial order relation

A binary relation R in a set P is called a partial order relation or a partial ordering in P iff R is reflexive, antisymmetric, and transitive.

Def. Poset

A set P together with a partial ordering R is called a partially ordered set or a poset.

Note: It is conventional to denote a partial ordering by the symbol <. This symbol does not necessarily mean "lessthan or equal to" as is used for real numbers.

Def. Totally ordered set.

Let (P, ) be a partially ordered set. If for every x, y Є P we have either x ≤ y V y ≤ x, then is called simple ordering or linear ordering on P and (P, ) is called a totally ordered or simply ordered set or a Chain

Example: The poset (Z, ≤) is totally ordered, since a ≤ b or b≤ a whenever a and b are integers.

Def. Let (P, ≤) be a partially ordered set and let A≤ P. Any element x Є P is an upper bound for A if for all a Є A, a ≤ x.

Similarly, any element x Є P is a lower bound for A if for all a Є A, x ≤ a

Def. Let (P, ) be a partially ordered set and let A ≤ P. Any element x Є P is a least upper bound or supremum, for A if x is an upper bound for A and x ≤ y where y is any upper bound for A. Similarly, then greatest lower bound, or infimum, for A is an element x Є P such that x is a lower bound and y ≤ x for all lower bounds y.

Def. Well-ordered

A partially ordered set is called well-ordered if every nonempty subset of it has a least member.

Def. Hasse diagram or partially ordered set diagram.

A partial ordering  ≤ on a set P can be represented by means of a diagram known as a Hasse diagram or a partially ordered set diagram of (P, ≤). In such a diagram, each element is represented by a small circle or a dot.

The circle for x Є P is drawn below the circle for y Є P if x <y, and a line is drawn between x and y if y covers x.

If x < y but y does not cover x, then x and y are not connected directly by a single line. However, they are connected through one or more elements of P. It is possible to obtain the set of ordered pairs in ≤ from such a diagram.

Example: Let P = {1, 2, 3, 4} and ≤ be the relation "lessthan or equal to" then the Hasse diagram is

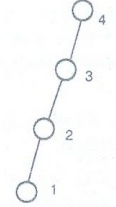
Note :

1. Hasse diagram, named after the twentieth - Century German mathematician Helmut Hasse.

2. In a digraph we apply the following rules then we get Hasse diagram.

(i) Each vertex of A must be related to itself. So the arrows from a vertex to itself are not necessary.

(ii) If a vertex b appears above vertex a and if vertex a is connected to vertex b by an edge, then aRb, so direction arrows are not necessary.

(iii) If vertex C is above a and if c is connected to a by a sequence of edges then arc.

(iv) The vertices are denoted by points rather than by circles.

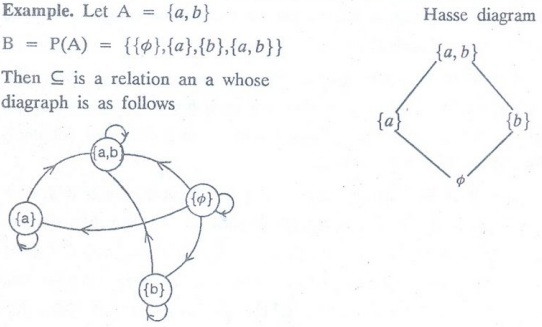
Then ≤ is a relation an a whose diagraph is as follows

Example 1. Show that the "greater than or equal" relation (≥) is a partial ordering on the set of integers.

Solution: Since a≥a for every integer a, ≥ is reflexive. If a ≥ b and b ≥ a, then a = b. Hence,  ≥ is antisymmetric. Finally, ≥ is transitive since a ≥ b and b ≥ c imply that a ≥ c. It follows ≥ that is a partial ordering on the set of integers and (Z, ≥) is a poset.

Example 3. Let R be a binary relation on the set of all positive integers such that R = {(a, b)/a b²)}. Is R reflexive ? Symmetric ? Antisymmetric ? Transitive? An equivalence relation? A partial ordering relation ? [MCA, MU, Nov. 1990, Dec. 1992]

Solution: R = {(a, b)/a, b are positive integers and a = b²}. For R to be reflexive, we should have a R a for all positive integers a. But a R a holds only when a = a² by hypothesis. Now a = a² is not true for all positive integers. Infact only for the positive integer a = 1, we have a = a². Hence R is not reflexive.

For R to be symmetric, if aRb then we should have b R a. But aRb implies a = b². But a = b² does not imply b = a² always for positive integers. For instance 16 = 4² but 4 ≠ 16². Hence aRb does not imply bRa. Hence R is not symmetric.

For R to be anti-symmetric, for positive integers a, b if a R, b and b R a hold, then a = b. aRb implies a = b² and bra implies b = a², So if a = b² and b = a², then a = b² = (a²)² = a⁴ i.e, a⁴ – a = 0, i.e., a (a³ − 1) = 0. Since a is not a positive integer, a ≠ 0 so that a³ – 1 = 0 i.e., a³ = 1 i.e., a = 1. This means b = a² = 1. Thus aRb and bRa imply a = b = 1. Hence R is anti-symmetric.

For R to be transitive, if aRb holds and bRc holds, the aRc should hold.

i.e., aRb implies a = b² and bRc implies b = c².

So that a = b² = c⁴. Hence aRc does not hold.

For example, 256 = 16² and 16 = 4² but 256 ≠ 4² (in fact 256=4⁴).Thus R is not transitive.

Also, R is not an equivalence relation as an equivalence relation is reflexive, symmetric and transitive. R is also not a partial ordering relation, as a partial ordering relation is reflexive, anti-symmetric and transitive.

Example 4. Let X = {2, 3, 6, 12, 24, 36} and the relation ≤ be such that x≤y if x divides y. Draw the Hasse diagram of (x, ≤)

Solution :

The relation

R = {(x, y)/x | y}, x ≤ y

= {(2, 6), (2, 12), (2, 24), (2, 36), (3, 6), (3, 12), (3, 24), (3, 36), (6, 12), (6, 24), (6, 36), (12, 24), (12, 36)}

The Hasse diagram is

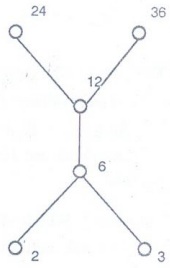
Example 6. Give a relation which is both a partially ordering relation and an equivalence relation on a set.

Solution: Equality, similarity of triangles are the examples of relation which are both a partial ordering relation and an equivalence relation.

Example 7. Which elements of the poset {{2, 4, 5, 10, 12, 20, 25}, |} are maximal, and which are minimal?

Solution: Draw Hasse diagram

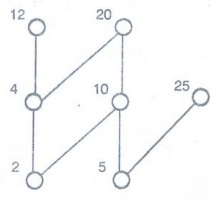
From the figure this poset shows that the maximal elements are 12, 20 and 25 and the minimal elements are 2 and 5. As this example shows, a poset can have more than one maximal element and more than one minimal element.

Example 8. Determine whether the posets represents by each of the Hasse diagrams in the following figure, have a greatest element and a least element.

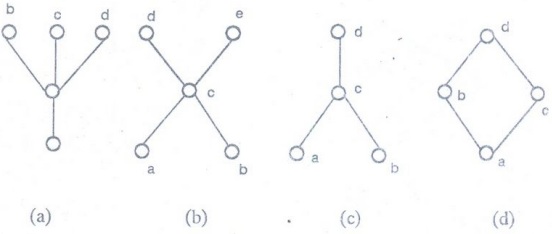
Solution: The least element of the poset with Hasse diagram (a) is a. This poset has no greatest element. The poset with Hasse diagram (b) has neither a least not a greatest element. The poset with Hasse diagram (c) has no least element. Its greatest element is d. The poset with Hasse diagram (d) has least element a and greatest element d.

Example 10. Is there a greatest element and a least element in the poset (Z⁺, 1) ?

Solution: The integer 1 is the least element since 1/n whenever n is a positive integer. Since then is no integer that is divisible by all positive integers, there is no greatest element.

Example 11. Draw the Hasse-diagram of the set of partitions of 5.

Solution :

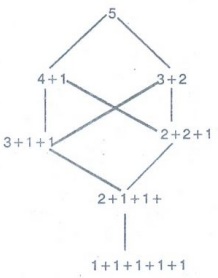
5 = 5

5 = 4+1

5 = 3+2

5 = 3+1+1

5 = 2+2+1

5 = 2+1+1+1

5 = 1+1+1+1+1

EXERCISE 5.1

1. Define Hasse diagram

2. Define totally ordered set with an example.

3. Define minimal and maximal elements of a poset.

4. Show that there are only five distinct Hasse diagrams for partially ordered sets that contain three elements.

5. Give an example of a set X such that (P(X), ≤) is a totally ordered set.

6. Let S denote the set of all the partial ordering relations on a set P. Define a partial ordering relation on S and interpret this relation in terms of the elements of P.

7. Draw the Hasse diagrams of the following sets under the partial ordering relation "divides" and indicate those which are totally ordered. {2, 6, 24}, {3, 5, 15}, {1, 2, 3, 6, 12}, {2, 4, 8, 16}, {3, 9, 27, 54}

8. If R is a partial ordering relation on a set X and A ≤  X, show that R ∩(A ˟ A) is a partial ordering relation on A.