Other Techniques for Uncertain Reasoning

Other Techniques for Uncertain Reasoning

AU: Dec.-14, 17, May-17

There are two basic reasons why probability can fail:-

1) One common view is that probability theory is essentially numerical, whereas human judgemental reasoning is more "qualitative".

2) Probabilistic Reasoning did not scale up because of the exponential number of probabilities required in the full joint distribution.

Default Reasoning

• We can do qualitative reasoning using technique like default reasoning.

• Default reasoning treats conclusions not as "believed to a certain degree", but as "believed until a better reason is found to believe something else".

Rule-based

1) This approach hope to build on the success of logical rule-based systems, but add a sort of "Fudge factor" to each rule to accommodate uncertainty. These methods were developed in the mid-1970s and formed the basis for a large number of expert systems in medicine and other areas.

2) Rule-based systems emerged from early work on practical and intuitive systems for logical inference.

3) Logical systems in general, and logical rule-based systems in particular have three desirable properties:

i) Locality: In logical systems, whenever we have a rule of the form A ⇒ B, we conclude B, given evidence A, without worrying about any other rules. In probabilistic systems, we need to consider all the evidence in the Markov blanket.

ii) Detachment: Once a logical proof is found for a proposition B, the proposition can be used regardless of how it was derived. That is, it can be detached from its justification. In dealing with probabilities, on the other hand, the source of the evidence for a belief is important for subsequent reasoning.

iii) Truth functionality: In logic, the truth of complex sentences can be computed from the truth of the components. Probability combination does not work this way, except under strong global independence assumptions.

4) There have been several attempts to devise uncertain reasoning schemes that retain these advantages. The idea is to attach degrees of belief to propositions and rules and to devise purely local schemes for combining and propagating those degrees of belief. The schemes are also truth functional.

For example: The degree of belief in A v B is a function of the belief in A and the belief in B.

5) Problem associated with rule based methods:-

i) The properties of locality, detachment, and truth-functionality are simply not appropriate for uncertain reasoning.

ii) Let us look at truth functionality first. Let H₁, be the event that a fair coin flip comes up heads. Let T₁ be the event that the coin comes up tails on that same flip, and let H₂ be the event that the coin comes up heads on a second flip. Clearly, all three events have the same probability, 0.5, and so a truth functional system must assign the same belief to the disjunction of any two of them. But we can see that the probability of the disjunction depends on the events themselves and not just on their probabilities.

It gets worse when we chain evidence together. Truth-functional systems have rules of the form A → B that allow us to compute the belief in B as a function of the belief in the rule and the belief in A. Both forward and backward-chaining systems can be devised. The belief in the rule is assumed to be constant and is usually specified by the knowledge engineer.

For example: as A →_0.9B

Consider the WetGrass situation. If we wanted to be able to do both causal and diagnostic reasoning, we would need the two rules,

Rain → WetGrass and WetGrass → Rain

These two rules form a feedback loop: evidence for Rain increases the belief in WetGrass, which in turn increases the belief in Rain even more. Clearly, uncertain reasoning systems need to keep track of the paths along which evidence is propagated.

Inter-causal reasoning (for explaining away) is also tricky. Consider what happens when we have the two rules,

Sprinkler → WetGrass and WetGrass → Rain.

Suppose we see that the Sprinkler is on. Chaining forward through our rules, this increases the belief that the grass will be wet, which in turn increases the belief that it is raining. But this is ridiculous; the fact that the sprinkler is on explains away the wet grass and should reduce the belief in rain. A truth functional system acts as if it also believes Sprinkler → Rain.

6) If task is restricted and rules are engineered carefully then truth-functional systems work well.

Ignorance

1) One area that we have not addressed so far is the question of ignorance, as opposed to uncertainty. Consider the flipping of a coin. If we know that the coin is fair, then a probability of 0.5 for heads is reasonable. If we know that the coinis biased, but we do not know which way, then 0.5 is the only reasonable gill b probability. The two cases are different, yet probability seems not to distinguish buy them. The Dempster-Shafer theory uses interval-valued degrees of belief to ow represent an agent's knowledge of the probability of a proposition.

2) Representing ignorance using Dempster-Shafer theory:-

i) The Dempster- Shafer theory is designed to deal with the distinction between uncertainty and ignorance.

ii) Rather than computing the probability of a proposition, it computes the probability that the evidence supports the propositions.

iii) This measure of belief is called a belief function, written Bel(X).

iv) We return to coin flipping for an example of belief functions. Suppose a shady character comes up to you and offers to bet you 10 that this coin will come up heads on the next flip. Given that the coin might or might not be fair, what belief should you ascribe to the event that it comes up heads? Dempster-Shafer theory says that because you have no evidence either way, you have to say that the belief Bel(Heads) = 0 and also that Bel(¬Heads) 0. This make Dempster-Shafer reasoning systems skeptical in a way that has some intuitive appeal.

v) Now suppose you have an expert at your disposal who testifies with 90% certainty that the coin is fair (i.e he is 90% sure that P(Heads) 0.5). Then Dempster-Shafer theory gives Bel(Heads) = 0.9×0.5 0.45 and likewise Bel (¬Heads) = 0.45. There is still a 10 percentage point "gap" that is not accounted for by the evidence.

vi) 'Dempster's rule' (Dempster, 1968) shows how to combine evidence to give new values for Bel, and Shafer's work extends this into a complete computational model.

vii) Problems associated with Dempster-Shafer theory:-

1. There is a problem in connecting beliefs to actions.

2. With probabilities, decision theory says that if P(Heads) = P(¬Heads) = 0.5 then (assuming that winning 10 and losing 10 are considered equal magnitude opposites). The reasoner will be indifferent between the action of accepting and declining the bet.

3. The Dempster-Shafer reasoner has Bel(¬ Heads) = 0 and thus no reason to accept the bet, but then it also has Bel(Heads) = 0 and thus no reason to decline it. Thus, it seems that the Dempster-Shafer reasoner comes to the same conclusion about how to act in this case.

4. Unfortunately, Dempster-Shafer theory allows no definite decision in many other cases where probabilistic inference does yield a specific choice.

viii) One inter-pretation of Dempster-Shafer theory is that it defines a probability interval, the interval for Heads is [0,1] before our expert testimony and [0.45, 0.55] after. The width of the interval might help in deciding when we need to acquire more evidence. It can tell you that the expert's testimony will help you if you do not know whether the coin is fair, but will not help you if already learned that the coin is fair. However, there are no clear guidelines for how to do this, because there is no clear meaning for what the width of an interval means.

ix) In the Bayesian approach, this kind of reasoning can be done easily by examining how much one's belief would change if one were to acquire more evidence.

For example: Knowing whether the coin is fair would have a significant impact on the belief that it will come up heads, and detecting an asymmetric weight would have an impact on the belief that the coin is fair. A complete Bayesian model would include probability estimates for factors such as these, allowing us to express our "ignorance" in terms of how our beliefs would change in the face of future information gathering.

7.4.4   Vagueness

• Probability makes the same ontological commitment as logic:- That events are true or false in the world, even if the agent is uncertain as to which is the case. Researchers in fuzzy logic have proposed an ontology that allows vagueness:- or That an event can be "Sort of" true. Vagueness and uncertainty are in fact orthogonal issues.

• Representing vagueness: (Fuzzy sets and fuzzy logic):

Fuzzy sets:

In standard set theory, an object is either a member of a set or it is not. There is no other choice. For example, 2, 4, 10, 16 are member of the set of even numbers but 15, Red, sky are not members.

Similarly, blue, white, red and black are members of the set of colors but match, house and vehicles are not members.

Traditional logics are based on the notions that P(a) is true as long as a is a member of the set belonging to class P and false otherwise. There is no partial containment. This amounts to the use of a characteristic function f from a set A, where f_A (X) = 1 if x is in A; otherwise it is 0.

Thus f is defined on the universe U and for all x € U, f: U→ {0, 1}.

This notion may be generalized by allowing this set to have a characteristic function assuming values other than 0 and 1.

For example, the notion of a fuzzy set is defined with the characteristic function u which maps from v to a number in the real interval [0, 1]; that is u : v→ [0, 1].

The concept of fuzzy sets:

Fuzzy set theory is used for specifying how well an object satisfies a vague description.

For example: Consider the proposition "Anil is tall". Is this true, if Anil is 5'10"? most people would hesitate to answer "true" or "false", preferring to say, "sort of".

Note that this is not a question of uncertainty about the external world. We are sure of Anil's height. The issue is that the linguistic term "tall" does not refer to a sharp demarcation of objects into two classes and there are degrees of tallness.

Due to this reason, fuzzy set theory is not a method for uncertain reasoning at all. Rather, fuzzy set theory treats Tall as a fuzzy predicate and says that the truth value of Tall(Anil) is a number between 0 and 1, rather than being just true or false.

The name "fuzzy set" derives from the interpretation of the predicate as implicitly defining a set of its members - a set that does not have sharp boundaries.

Definition - Fuzzy set Ā:

Definition: Let U be a set, denumerable or not and let x be an element of U. A fuzzy subset Ā of U is a set of ordered pairs {(x, u_A (x))3}, for all x in U₁ where u_A (x) is a membership characteristic function with values in [0, 1] and which indicates the degree or level of membership of x in Ā.

Here, u_A (x) = 0 indicates that x is not in Ā.

U_A (x) = 1 signifies that x is completely contained in Ā.

Values of 0 < U_A (x) < 1 signify that x is a partial member of A.

Fuzzy characteristic function relates to vagueness and is a measure of the feasibility or ease of attainment of an event. Fuzzy sets have been related to possibility distributions which have some similarities to probability distributions, but their meanings are entirely different.

Now, consider an example, where fuzzy set is defined as,

Ā = { tall }

and assign values

u_A (0) = u_A (10) = ....= u_A (40) = 0

u_A (50)= 0.2

u_A (60) = 0.4

u_A (70)= 0.6

u_A (80) = 0.9

u_A (90) = u_A (100) = 1.0.

and TALL (Joe)= 0.5

One should also assign values to other fuzzy sets associated with linguistic variables such as very short, short, medium etc.

So, by this one can conclude that now there is a means of expressing the notion of TALL(x) for an individual x.

Operations on fuzzy sets and properties of fuzzy sets:

Operations on fuzzy sets are somewhat similar to the operations of standard set theory, as given below -

1. Equality – A  B if and only if U_A (x) = U_B (x) for all x ϵ U

2. Containment - A  B if and only if U_A (x) ≤ U_B (x) for all x ϵ U

3. Intersection - U_A∩B(x) = min{U_A (x), U_B (x)}

4. Union - U_AUB (X) = Max_x {U_A (x), U_B (x)}

5. Complement set - U_A (x) = 1-U_A (x)

• Here, single quotation mark denotes the complement fuzzy set, A'.

• Intersection of two fuzzy sets Ā and  is the largest fuzzy subset that is a subset of both.

• Similarly, the union of two fuzzy sets Ā and  is the smallest fuzzy subset having both Ā and  as subsets.

• By applying above operations on fuzzy sets, the properties that can be derived, which are applicable of fuzzy sets are as follows -

Since in general for u_A (x) = a, with 0 < a < 1, we have

i) u_AUA' (x) = max [a, 1 - a] ≠ 1

and ii) u_A∩A'(x)=min [a, 1 a] ≠ 0

On the other hand the following relations do hold

i) Ā∩ϕ = ϕ

ii) Ā U ϕ = Ā

iii) Ā ∩ U = Ā

and iv) Ā U U = U

• The universe from which a fuzzy set is constructed may also be uncountable. For example, one can define values of u for the fuzzy set

Ā = {young} as

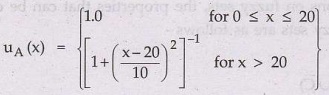
The values of U_A (x) are depicted graphically in Fig. 7.4.1

• Except above defined operations there are some operations that are unique to fuzzy sets only. Some of these are as follows -

i) Dilation - The dilation of Ā is defined as

DIL (Ā) = [u_A (x)]^1/2 for all x in U.

ii) Concentration - The concentration of Ā is defined as

CON (Ā) = [u (x)]² for all x in U.

iii) Normalization - The normalization of Ā is defined as

NORM (Ā) = U_A (x)/Max_x {u_A (x)}

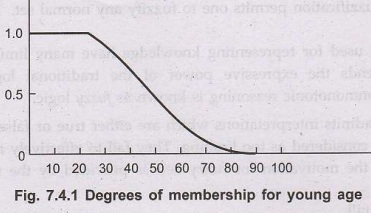
for all x in U. These operations are shown in Fig. 7.4.2.

Dilation tends to increase the degree of membership of all partial members x by spreading out the characteristic function curve.

The concentration is the opposite of dilation. As it tends to decrease the degree of membership of all partial members and concentrates the characteristic function curve.

While normalization provides a means of normalizing all characteristic functions to the same base much the same as vectors can be normalized to unit vectors.

Fuzzification - Fuzzification permits one to fuzzify any normal set.

• Fuzzy logic:

Traditional logics used for representing knowledge have many limitations. So a new method, which extends the expressive power of the traditional logics and permits different forms of non monotonic reasoning is known as fuzzy logic.

Traditional logic admits interpretations which are either true or false only. The use of two valued logics is considered as too limiting. They fail to effectively represent value or fuzzy concepts, i.e., the motivation for fuzzy sets is provided by the need to represent such propositions as –

- Radha is very tall.

- Rima is slightly ill.

- Ram and Shyam are close friends.

- Exceptions to the rules are nearly impossible.

- Most chinese are not very tall.

While traditional set theory defines set membership as a Boolean predicate, fuzzy set theory allows us to represent set membership as a possibility distribution. Consider an example of fuzzy logic.

Suppose, one want to make distinction between a tall person and a short heighted person. No doubt one would be willing to agree that the predicate "TALL" is true for pole, the seven foot basketball player and false for smidge the midget. But what value you would assign for Ram, who is 5 foot 10 inches? What about Raju who is 6 foot 2 or Joe who is 5 foot 5?

If one agrees 7 foot is tall, then 6 foot 2 or Raj who is 5 foot 5? If one agree 7 foot is tall, then is 6 foot 11 inches also tall? What about 6 foot 10 inches?

If continued this process of incrementally decreasing the height through a sequence of applications of modus ponens, one would eventually, conclude that a three foot person is tall. Intuitively, one expects the inferences should have failed at some point, but at what point? In FOPL there is no direct way to represent this type of concept. 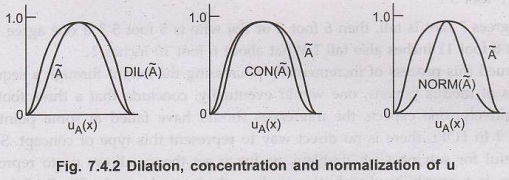So, fuzzy logic is useful for solving such problem, as fuzzy set theory allows us to represent set membership as a possibility distribution such as the ones shown in Fig. 7.4.3 for the set of tall people and the set of very tall people shown in Fig. 7.4.4.

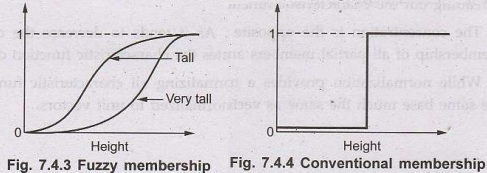
In the latter, one is either tall or not and there must be a specific height that defined the boundary. The same is true for very tall.

In the former ones tallness increased with one's height until the value of 1 is reached. Fuzzy logic is a method for reasoning with logical expressions describing membership in fuzzy sets. For example: The complex sentence Tall (Anil) Heavy (Anil) has Λ truth value that is a function of the truth values of its components.

The standard rules for evaluating the fuzzy truth, T, of a complex sentence are

T (A ^ B) = min (T(A), T(B))

T (A v B) = max (T(A), T(B))

T(¬A) = 1 - T(A)

Fuzzy logic is therefore a truth-functional system - a fact that causes serious difficulties.

For example: Suppose that T (Tall(Anil)) = 0.6 and T (Heavy(Anil)) = 0.4. Then we have T (Tall(Anil)) ^ T (Heavy (Anil)) = 0.4. Which seems reasonable but we also get the result T (Tall(Anil)) ^ ¬ (Tall(Anil)) 0.4 which does not. The problem arises from the inability of a truth-functional approach to take into account the correlations or anti-correlations among the component propositions.

Benefits of fuzzy logic over classical probability theory:

According to Zadeh classical probability theory lack in following ways -

1) Classical probability theory is insufficient to deal with uncertainty.

2) Classical probability theory has no facilities for representing the meaning of events containing -

i)  Fuzzy predicates such as small, large, young, safe, much longer than, soon.

ii) Fuzzy quantifiers such as most, means, few, several, often, usually.

iii) Fuzzy probabilities expressed as quite possible, almost impossible etc.

iv) Fuzzy truth values such as very quite, extremely, somewhat, slightly.

Lacking these facilities, one finds it is difficult to deal with statements like –

i) More the cholesterol, more is the chance for heart attack.

ii) Almost all people prefer a strong union government.

iii) It is very likely that Radha is young.

iv) Ram is much taller than most of the friends.

Now, to overcome above problems one can use fuzzy logic. Consider an example, where fuzzy is used -

Suppose, you have been asked by your friends to arrange a small party. Now here the question is "what does 'small' mean?". Answer to this question is different for persons of different societies. As if you are affluent, small has one meaning and if you belong to middle class family, the word small has a different meaning. Hence, one can say that sets for whom the boundary is ill-defined are called fuzzy sets.

Now, the question arises that how can one represent a fuzzy set if the boundary is not clear. This can be done by grade membership diagram. All the member of a fuzzy set have a membership value between 0 {complete nonmembership) and 1 (complete membership).

For this consider a fuzzy set "small numbers" like "small party". The number that has the minimal value (i.e. zero) is the smallest number and hence the membership value is 1. A number increases, the value of "small" decreases and at a point of the time the value reaches zero.

This is shown in Fig. 7.4.5.

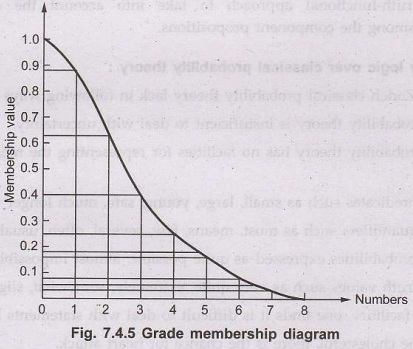
From this curve, one can find the membership value or in other words the element is a member of the set to some degree.

Reasoning using fuzzy logic:

In fuzzy logic, the degree of membership of x is Ā, where Ā defines some propositional or predicate class. When U_A (x) = 1, the proposition A is completely true and when U_A (x) 0 it is completely false. Values between 0 and 1 assumes corresponding values of truth or falsehood.

Truth value of a statement can be found by using truth tables. But in case of fuzzy logic it is not possible as there may be infinite number of truth values and one could tabulate only a limited number of truth values, as those corresponding to the terms false, not very false, not true, very true and so on.

So, here one has an inference rule equivalent to a fuzzy modus ponens. Modus ponens for fuzzy sets are different from standard modus ponens in that statements which are characterized by fuzzy sets are permitted and the conclusion need not be identical to the implicand in the implication.

For example, let Ā, Ā₁,  and 1 be statements characterized by fuzzy sets. Then one form of the generalized modus ponens reads

Premise: x is Ā₁

Implication:If x is Ā then y is 

Conclusion: y is 1

An example of this form of modus ponens is given as -

Premise: This man is very brilliant.

Implication: If a man is brilliant then the man is intelligent.

Conclusion: This man is very intelligent.

According to Zadeh's a relation can be defined as -

Relation - For two sets A and B, the cartesian product A × B is the set of all, ordered pairs (a, b) for a  A and b  B.

A binary relation of two sets A and B is a subset of A × B.

Binary fuzzy relation - Binary fuzzy relation R is a subset of fuzzy cartesian product Ā × , a mapping of Ā →  characterized by the two parameter membership function U_R (a, b).

For example, let Ā →  = R the set of real numbers and let R: = much larger than. A membership function for this relation might then be defined as –

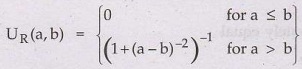
Now, let X and Y be two universes and let Ā and  be fuzzy sets in X and X × Y respectively.

Define fuzzy relations Ṝ_A (x), Ṝ_B (x, y)and Ṝ_C(y) in X, X × Y and Y respectively.

Then the compositional rule of inference is the solution of the relation equation. Ṝ_c(y) = Ṝ_A (x) O Ṝ_B (x, y) = max_x min{u_A (X), u_B (x, y)}

where the symbol O signifies the composition of Ā and  as an example.

Let,

x = y = {1, 2, 3, 4}

Ā = {little} = {(1/1), (2/0.6), (3/0.2), (4.0/0)}

Ṝ = Approximately equal, a fuzzy relation defined by

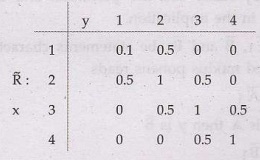
Then applying the max-min composite rule

Ṝ_C (y) = max_x min{u_A (x), U_R (x, y)}

= max_x {min[(1, 1), (0.6, 0.5), (0.2, 0), (0, 0)]},

= min[(1, 0.5), (0.6, 1), (0.2, 0.5), (0, 0)]

=min[(1, 0), (0.6, 0.5), (0.2, 1), (0, 0.5)]

= min[(1, 0), (0.6, 0), (0.2, 0.5), (0, 1)],

= max_x {[1, 0.5, 0, 0], [0.5, 0.6, 0.2, 0], [0, 0.5, 0.2, 0], [0, 0, 0.2, 0]}

= {[1], [0.6], [0.5], [0.2] }

Therefore the relation is

Ṝ_C (y) = ((1/1), (2/0.6), (3/0.5), (4/0.2)}

Stated in terms of a fuzzy modus ponens, one might interpret this as the inference.

- Premise: x is little

- Implication: x and y are approximately equal

- Conclusion: y is more or less little

The above notion can be generalized to any number of universes by taking the cartesian product and defining relations on various subsets.

Applications of fuzzy logic:

One of the recent applications where fuzzy logic has been extensively used is development of fuzzy logic controlled commercial air-conditioner by Mitsubishi Heavy Industries of Japan.

Conventional air-conditioners have an annoying and discomforting characteristic of turning ON and OFF when the temperature exceeds or falls below a fixed temperature. Fuzzy based air-conditioners determines the thermal characteristic of the room and temperature change required and adjusts the air flow to minimize heating and cooling times and maintain a stable room temperature.

An infra-red sensor in the equipment determines if anyone is there in the room. If not, the system gradually reduces the air flow and temperature, thereby minimizing power consumption.

The air-conditioner equipment is only the tip of the iceberg where fuzzy logic is used. In future, many such equipment are expected.

Fuzzy logic can be represented in terms of probability theory. One idea is to view assertions such as "Anil is Tall" as discrete observations, made concerning a continuous hidden variable, Anil's actual height. The probability model specifies P(observer says Anil is tall/Height), using a probit distribution. A posterior distribution over Anil's height can then be calculated in the usual way, for example if the model is part of a hybrid Bayesian Network.

• Fuzzy control:

1. Fuzzy control is methodology for constructing control systems in which the mapping between real-valued input and output parameters is represented by fuzzy rules.

2. Fuzzy control has been very successful in commercial products such as automatic transmissions, video cameras, and electric shavers.

3. These applications enjoy success may be because they have small rule bases, no chaining of inferences and tunable parameters that can be adjusted to improve the system's performance. The fact that they are implemented with fuzzy operators might be incidental to their success; the key is simply to provide a concise and intuitive way to specify a smoothly interpolated, real-world function.

Fuzzy predicates can also be given a probabilistic interpretation in terms of random sets - that is, random variables whose possible values are sets of objects.

For example: Tall is random set whose possible values are sets of people. The probability P(Tall = S₁), where S₁ is some particular set of people, is the probability that exactly the set would be identified as "tall" by an observer. Then the probability that "Anil is tall" is the sum of the probabilities of all the sets of which Anil is a member.

Both the hybrid Bayesian network approach and the random sets approach appear to capture aspects of fuzziness without introducing degrees of truth. But they can not handle proper representation of linguistic observations and continuous quantities that have been neglected by most outside the fuzzy community.