Operations on Arrays

OPERATIONS ON ARRAYS

There are a number of operations that can be preformed on arrays. These operations include:

• Traversing an array

• Inserting an element in an array

• Deleting an element from an array

• Merging two arrays

• Searching an element in an array

• Sorting an array in ascending or descending order

We will study all these operations in detail in this section.

Traversing an Array

Traversing an array means accessing each and every element of the array for a specific purpose.

If A is an array of homogeneous data elements, then traversing the data elements can include printing every element, counting the total number of elements, or performing any process on these elements. Since an array is a linear data structure (because all its elements form a sequence), traversing its elements is very simple and straightforward. The algorithm for array traversal is given in Figure 5.9.

In Step 1, we initialize index to the lower bound of the array. In Step 2, a while loop is executed. Steps 3 and 4 form part of the loop. Step 3 processes the individual array element as specified by the array name and index value. Step 4 increments the index value so that the next array element could be processed. The while loop in Step 2 is executed until all the elements in the array are processed. In other words, the while loop will be executed until i is less than or equal to the upper bound of the array.

Example 5.4

Assume that there is an array Marks[ ], such that the index of the array specifies the roll number of the student and the value of a particular element denotes the marks obtained by the student. For example, if it is given Marks[4] =78, then the student whose roll number is 4 has obtained 78 marks in the examination. Now, write an algorithm to:

(a) Find the total number of students who have secured 80 or more marks.

(b) Print the roll number and marks of all the students who have got distinction.

Solution

(a) Step 1: [Initialization] Set Count = 0, I = lower­­­­_bound

Step 2: Repeat for I = lower_bound to upper_bound

IF Marks [I] >= 80, then: Set Count = Count + 1

[End of IF]

Set I = I + 1

[END OF LOOP]

Step 3: Exit

(b) Step 1: [Initialization] Set I = lower_bound

Step 2: Repeat for I = lower_bound to upper_bound

IF Marks [I] >= 75, Write: I,

Marks [I]

[End of IF]

Set I = I + 1

[END OF LOOP]

Step 3: Exit

1. Write a program to read and display n numbers using an array.

#include <stdio.h>

#include <conio.h>

int main()

{

int i=0,n,arr [20];

clrscr();

printf("\n Enter the number of elements: ");

scanf("%d", &n);

printf("\n Enter the elements");

for (i=0;i<n;i++)

{

printf("\n Arr [%d] = ", i);

scanf("%d", &arr [i]);

}

printf("\n The array elements are \n");

for (i=0;i<n;i++)

printf("Arr [%d] = %d\t", i, arr[i]);

return 0;

}

Output

Enter the number of elements: 5

Enter the elements

Arr [0] = 1

Arr [1] = 2

Arr [2] = 3

Arr [3] = 4

Arr [4] = 5

The array elements are

Arr [0] = 1 Arr [1] = 2 Arr [2] = 3

Arr [3] = 4 Arr [4] = 5

2. Write a program to read and display n random numbers using an array.

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#define MAX 10

int main()

{

int arr [MAX], i, RandNo;

for (i=0;i< MAX; i++)

{

/* Scale the random number in the range 0 to MAX-1 */

RandNo = rand()% MAX;

// rand() is a pre-defined function

arr[i] = RandNo;

}

printf("\n The contents of the array are: \n");

for (i=0; i<MAX; i++)

printf("\t %d", arr[i]);

getch();

return 0;

}

Output

The contents of the array are:

6 0 8 4 7 1 0 2 7 3

3. Write a program to print the position of the smallest of n numbers using arrays.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, arr[20], small, pos;

clrscr();

printf("\n Enter the number of elements in the array: ");

scanf("%d", &n);

printf("\n Enter the elements: ");

for (i=0;i<n;i++)

scanf("%d", &arr [i]);

small=arr [0]; pos=0;

for(i=1;i<n;i++)

{

if (arr[i] <small)

{

small = arr[i];

pos = i;

}

}

printf("\n The smallest element is : %d", small);

printf("\n The position of the smallest element in the array is: %d", pos);

return 0;

}

Output

Enter the number of elements in the array: 5

Enter the elements: 1 2 3 4 5

The smallest element is: 1

The position of the smallest element in the array is: 0

4. Write a program to interchange the largest and the smallest number in the array.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, arr [20], temp;

int small, small_pos;

int large, large_pos;

clrscr();

printf("\n Enter the number of elements :");

scanf("%d", &n);

for(i=0;i<n;i++)

{

printf("\n Enter the value of element%d: ",i);

scanf("%d", &arr [i]);

}

Small=arr[0];

small_pos=0;

large=arr [0];

large_pos=0;

for(i=1;i<n;i++)

{

if (arr[i] <small)

{

small = arr[i];

small 1_pos = i;

}

if (arr[i] >large)

{

large arr[i];

large_pos = i;

}

}

printf("\n The smallest of these numbers is : %d", small);

printf("\n The position of the smallest number in the array is: %d", small_ pos);

printf("\n The largest of these numbers is: %d", large);

printf("\n The position of the largest number in the array is: %d", large_ pos);

temp = arr [large_pos];

arr [large_pos] = arr [small_pos];

arr[small_pos] = temp;

printf("\n The new array is: ");

for (i=0;i<n;i++)

printf("\n %d ", arr[i]);

return 0;

}

Output

Enter the number of elements: 5

Enter the value of element 0:1

Enter the value of element 1:2

Enter the value of element 2:3

Enter the value of element 3:4

Enter the value of element 4:5

The smallest of these numbers is : 1

The position of the smallest number in the array is: 0

The largest of these numbers is: 5

The position of the largest number in the array is: 4

The new array is:

5 2 3 4 1

5. Write a program to find the second largest number using an array of n numbers.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, arr[20], pos, large, second_large;

clrscr();

printf("\n Enter the number of elements in the array: ");

scanf("%d", &n);

for (i=0;i<n;i++)

{

printf("\n Enter the number: ");

scanf("%d", &arr[i]);

}

large=arr [0] ;pos=0;

for (i=1;i<n;i++)

{

if (arr[i]>large)

{

large = arr[i];

pos=i;}

}

second_large=arr [n-pos-1];

for (i=0;i<n;i++)

{

if (i!= pos)

{

if (arr[i] >second_large)                                            

second_large = arr[i];

}

}

printf("\n The numbers you entered are: ");

for (i=0;i<n;i++)

printf("%d ", arr[i]);

logo printf("\n The largest of these numbers is: %d", large);

printf("\n The second largest of these numbers is: %d", second_large);

return 0;

}

Output

Enter the number of elements in the array: 5

Enter the number: 1

Enter the number: 2

Enter the number: 3

Enter the number: 4

Enter the number: 5

The numbers you entered are:

1 2 3 4 5

The largest of these numbers is: 5

The second largest of these numbers is: 4

6. Write a program to enter n number of digits. Form a number using these digits.

#include <stdio.h>

#include <conio.h>

#include <math.h>

{

int main()

int number=0, digit [10], numofdigits,i;

clrscr();

printf("\n Enter the number of digits: ");

scanf("%d", &numofdigits);

for (i=0;i<numofdigits; i++)

{

printf("\n Enter the %dth digit: ", i);

 scanf("%d", &digit [i]);

}

i=0;

while (i<numofdigits)

{

number = number digit [i]* pow (10, i);

i++;

}

printf("\n The number is: %d", number);

return 0;

}

Output

Enter the number of digits: 3

Enter the 0th digit: 3

Enter the 1th digit: 4

Enter the 2th digit: 5

The number is: 543

7. Write a program to find whether the array of integers contains a duplicate number.

#include <stdio.h>

#include <conio.h>

int main()

{

int array [10], i, n, j, flag=0;

clrscr();

printf("\n Enter the size of the array: ");

scanf("%d", &n);

printf("\n Enter the elements: ");

for (i=0;i<n;i++)

{

scanf("%d", &array[i]);

for (i=0;i<n;i++)

{

for(j=i+1;j<n;j++)

{

if (array[i] == array [j] && i!=j)

{

flag=1;

printf("\n Duplicate numbers found at location %d and %d", i, j);

}

}

}

if(flag==0)

printf("\n No Duplicate");

return 0;

}

Output

Enter the size of the array: 5

Enter the elements: 1 2 3 4 5

No Duplicate

8. Write a program to read marks of 10 students in the range of 0-100. Then make 10 groups: 0-10, 10-20, 20-30, etc. Count the number of values that falls in each group and display the result.

#include <stdio.h>

#include <conio.h>

int main()

{

int marks [50], i;

int group [10]={0};

printf("\n Enter the marks of 10 students: \n");

for (i=0;i<10; i++)

{

printf("\n MARKS [%d] = ", i);

scanf("%d", &marks [i]);

++group [(int) (marks [i])/10];

}

printf("\n\n ****************");

printf("\n GROUP \t\t FREQUENCY");

for (i=0;i<10;i++)

printf("\n %d \t\t%d", i, group [i]);

getch();

return 0;

}

Output

Enter the marks of 10 students:

MARKS [0] = 95

MARKS [1] = 88

MARKS [2] = 67

MARKS [3] = 78

MARKS [4] = 81

MARKS [5] = 98

MARKS [6] = 55

MARKS [7] = 45

MARKS [8] = 72

MARKS [9] = 90

******************

GROUP FREQUENCY

0                 0

1                 0

2                 0

3                 0

4                 1

5                 1

6                 1

7                 2

8                 2

9                 3

9. Modify the above program to display frequency histograms of each group.

#include <stdio.h>

int main()

{

int marks [10], i, index;

int group [10]={0};

printf("\n Enter the marks of 10 students : \n");

for (i=0;i<10;i++)

{

printf("\n MARKS [%d] = ", i);

scanf("%d", &marks [i]);

++group [(int) (marks[i])/10];

}

printf("\n\n ****************");

i=0;

printf("\n\n FREQUENCY HISTOGRAM");

for (index=0; index<10; index++)

{

printf("\n GROUP %d |", index);

for (i=0; i<group [index]; i++)

printf(" * ");

}

getch();

return 0;

}

Output

Enter the marks of 10 students:

MARKS [0] = 95

MARKS [1] = 88

MARKS [2] = 67

MARKS [3] = 78

MARKS [4] = 81

MARKS [5] = 98

MARKS [6] = 55

MARKS [7] = 45

MARKS [8] = 72

MARKS [9] = 90

*************************

FREQUENCY HISTOGRAM

GROUP 0 |

GROUP 1 |

GROUP 2 |

GROUP 3 |

GROUP 4 | *

GROUP 5 | *

GROUP 6 | *

GROUP 7 | **

GROUP 8 | **

GROUP 9 | ***

10. Write a program to read a sorted list of floating point values and then calculate and display the median of the values.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, j, n;

float median, values [10];

printf("\n Enter the size of the array: ");

scanf("%d", &n);

printf("\n Enter the values: ");

for (i=0; i<n;i++)

scanf("%f", &values [i]);

if (n%2==0)

median = (values [n/2] + values [n/2+1])/2.0;

else

median = values [n/2 + 1];

printf("\n MEDIAN%.2f", median);

getch();

return 0;

}

Output

Enter the size of the array: 5

Enter the values:

12 34 56 78 89

MEDIAN = 56.00

Inserting an Element in an Array

Inserting an element in array means adding a new data element to an already existing array. If the element has to be inserted at the end of the existing array, then the task of inserting is quite simple. We just have to add 1 to the upper_bound and assign the value. Here we assume that the memory space allocated for the array is still available. For example, if an array is declared to contain 10 elements, but currently it is having only 8 elements, then obviously there is space to accommodate two more elements. But if it already has 10 elements, then we will not be able to add another element to it.

Figure 5.10 shows an algorithm to insert a new element to the end of the array.

In Step 1, we increment the value of the upper_bound.

In Step 2, the new value is stored at the position pointed by upper_bound.

For example, if we have an array that is declared as

int marks [60];

The array is declared to store marks of all the students in the class. Now suppose there are 54 students and a new student comes and is asked to give the same test. The marks of this new student would be stored in marks [55]. Assuming that the student secured 68 marks, we will assign the value as,

marks [55] = 68;

However, if we have to insert an element in the middle of the array, then this is not a trivial task. On an average, we might have to move as much as half of the elements from their position in order to accommodate space for the new element.

For example, consider an array whose elements are arranged in ascending order. Now, if a new element has to be added, it will have to be added probably somewhere in the middle of the array. To do this, we will have to first find the location where the new element will be inserted and then move all the elements (that have a value greater than that of the new element) one space to the right so that space can be created to store the new value.

Example 5.5

Data [] is an array that is declared as int Data [20]; and contains the following values:

Data[] = {12, 23, 34, 45, 56, 67, 78, 89, 90, 100};

(a) Calculate the length of the array.

(b) Find the upper bound and lower bound.

(c) Show the memory representation of the array.AM

(d) If a new data element with value 75 has to be inserted, find its position.

(e) Insert the new data element and then show the memory representation of the array.

Solution

(a) Length of the array = number of elements Therefore, length of the array = 10

(b) By default, lower_bound

(c)

(d) Since the elements of the array are stored in ascending order, the new data element will be stored after 67, i.e., at the 6th location. So, all the array elements from the 6th position will be moved one location towards the right to accommodate the new value.

(e)

Algorithm to insert an element in the middle of an array

The algorithm INSERT will be declared as INSERT (A, N, POS, VAL). The arguments are

(a) A, the array in which the element has to be inserted (b) N, the number of elements in the array

(c) POS, the position at which the element has to be inserted and

(d) VAL, the value that has to be inserted.

In the algorithm given in Figure 5.11, in Step 1, we first initialize I with the total number of elements in the array. In Step 2, a while loop is executed which will move all the elements that have index greater than POS one position towards right to create space for the new element. In Step 5, we increment the total number of elements in the array by 1 and finally in Step 6, the new value is inserted at the desired position.

Now, let us visualize this algorithm by taking an 1001 example. Initial Data [] is given as shown in Figure 5.12. Calling INSERT (Data, 6, 3, 100) will lead to the following processing in the array:

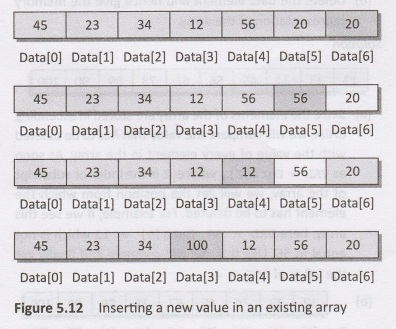
11. Write a program to insert a number at a given location in an array.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, num, pos, arr [10];

clrscr();

printf("\n Enter the number of elements in the array: ");

scanf("%d", &n);

printf("\n Enter the values");

for (i=0;i<n;i++)

{

scanf("%d", &arr[i]);

}

printf("\n Enter the number to be inserted: ");

scanf("%d", &num);

to printf("\n Enter the position at which the number has to be added: ");

scanf("%d", &pos);

for (i=n-1;i>=pos; i--)

arr[i+1] = arr[i];

arr [pos] = num;

n++;

printf("\n The array after insertion of %d is: ", num);

for (i=0;i<n;i++)

printf("\t %d", arr[i]);

getch();

return 0;

}

Output

Enter the number of elements in the array: 5

Enter the values: 1 2 3 4 5

Enter the number to be inserted: 7

Enter the position at which the number has to be added: 3

The array after insertion of 7 is:

1 2 3 7 4 5

12. Write a program to insert a number in an array that is already sorted in ascending order.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, j, num, arr [10];

clrscr();

printf("\n Enter the number of elements in the array: ");

scanf("%d", &n);

printf("\n Enter the array elements: ");

for (i=0;i<n;i++)

scanf("%d", &arr[i]);

printf("\n Enter the number to be inserted: ");

scanf("%d", &num);

for(i=0;i<n;i++)

{                             

if (arr[i] > num)

{

for (j = n-1; j>=i; j--)

arr[j+1] = arr[j];

arr[i] = num;

break;

}

}

n++;

printf("\n The array after insertion of %d is: ", num);

for (i=0;i<n;i++)

printf("\t %d", arr[i]);

getch();

return 0;

}

Output

Enter the number of elements in the array: 5

Enter the array elements:

1 2 3 4 5

Enter the number to be inserted: 6

 The array after insertion of 6 is:

1 2 3 4 5 6

Deleting an Element from an Array

Deleting an element from an array means removing a data element from an already existing array. If the element has to be deleted from the end of the existing array, then the task of deletion is quite simple. We just have to subtract 1 from the upper_bound. Figure 5.13 shows an algorithm to delete an element from the end of the array.

For example, if we have an array that is declared as

int marks [];

The array is declared to store marks of all the students in the class. Now suppose there are 54 students and the student with roll number 54 leaves the course. The marks of this student was therefore stored in marks [54]. We just have to decrement the upper_bound. Subtracting 1 from the upper_bound will indicate that there are 53 valid data in the array.

However, if we have to delete the element from the middle of the array, then this task is not trivial. On an average, we might have to move as much as half of the elements from their position in order to occupy the space of the deleted element.

For example, consider an array whose elements are arranged in ascending order. Now, if an element has to be deleted from somewhere middle of the array. To do this, we will first find the location from where the element has to be deleted and then move all the elements (that have a value greater than that of the element) one location towards the left so that location vacated by the deleted element is occupied by rest of the elements.

Example 5.6

Data [] is an array that is declared as int Data [10]; and contains the following values:

Data[] = {12, 23, 34, 45, 56, 67, 78, 89, 90, 100};

(a) If a data element with value 56 has to be deleted, find its position.

(b) Delete the data element and hence give the memory representation of the array.

Solution

(a) Since the elements of the array are stored in ascending als order, we will compare the value that has to be deleted with the value of every element in the array. As soon as VAL = Data [I], where I is the index or subscript of the array, we will get the position from which the element has to be deleted. For example, if we see this array, here VAL = 56. Data [0] = 12 which is not equal to 56. Like this, we will compare and finally get the value of POS = 4.

Algorithm to delete an element from the middle of an array

The algorithm DELETE will be declared as DELETE (A, N, POS). The arguments are as follows:

(a) A, the array from which the element has to be deleted (b) N, the number of elements in the array

(c) POS, the position from which the element has to be deleted

Figure 5.14 shows the algorithm in which we first initialize I with the position from which the element has to be deleted. In Step 2, a while loop is executed which will move all the elements that have index greater than POS one location towards left to occupy the location vacated by the deleted element. When we say that we are deleting an element, we are actually overwriting the element with the value of its successive element. In Step 5, we decrement the total number of elements in the array by 1.

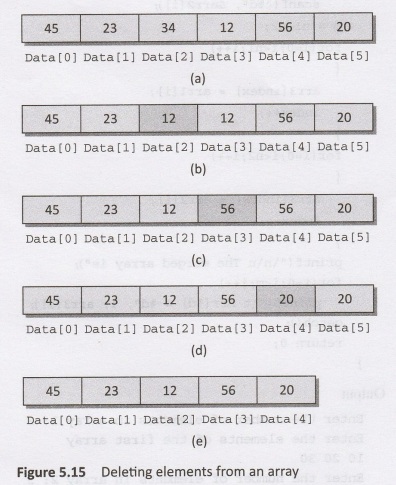
Now, let us visualize this algorithm by taking an example and having a look at Figure 5.15. Initial Data [] is given as shown in Figure 5.15. Calling DELETE (Data, 6, 2) will lead to the following processing in the array:

13. Write a program to delete a number from a given location in an array.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, pos, arr [10];

clrscr();

printf("\n Enter the size of the array: ") i

scanf("%d", &n);

printf("\n Enter the elements of the array: ");

for (i=0;i<n;i++)

scanf("%d", &arr[i]);

printf("\n Enter the position from which the number has to be deleted: ");

scanf("%d", &pos);

for (i= pos; i<n-1;i++)

arr[i] = arr [i+1];

n--;

printf("\n The array after deletion is: ");

for (i=0;i<n;i++)

printf("\n Arr [%d] = %d", i, arr[i]);

getch();

return 0;

}

Ouput

Enter the size of the array: 5

Enter the elements of the array:

1 2 3 4 5

Enter the position from which the number has to be deleted: 3

The array after deletion is:

Arr [0] = 1

Arr [1] = 2

Arr [2] = 3

Arr [3] = 5

14. Write a program to delete a number from an array that is already sorted in ascending order.

#include <stdio.h>

#include <conio.h>

int main()

{

int i, n, j, num, arr [10];

clrscr();

printf("\n Enter the number of elements in the array : ");

scanf("%d", &n);

printf("\n Enter the elements: ");

for (i=0;i<n;i++)

scanf("%d", &arr [i]);

printf("\n Enter the number to be deleted: ");

scanf("%d", &num);

for (i=0;i<n;j++)

{

if (arr[i] = = num)

{

for(j=i; j<n-1;j++)

arr[j] = arr[j+1];

}

}

printf("\n The array after deletion is:");

for (i=0;i<n-1;i++)

printf("\t%d", arr[i]);

getch();

return 0;

}

Output

Enter the number of elements in the array:

5

Enter the elements: 1 2 3 4 5

Enter the number to be deleted: 3

The array after deletion is: 1 2 4 5

Merging Two Arrays

Merging two arrays in a third array means first copying the contents of the first array into the third array and then copying the contents of the second array into the third array. Hence, the merged array contains contents of the first array followed by the contents of the second array.

If the arrays are unsorted then merging the arrays is very simple as one just needs to copy the contents of one array into another. But merging is not a trivial task when the two arrays are sorted and the merged array also needs to be sorted. Let us first discuss the merge operation on unsorted arrays. This operation is shown in Figure 5.16.

15. Write a program to merge two unsorted arrays.

#include <stdio.h>

#include <conio.h>

int main()

{

int arr1 [10], arr2 [10], arr3 [20];

int i, n1, n2, m, index=0;

clrscr();

printf("\n Enter the number of elements in array 1: ");

scanf("%d", &n1);

printf("\n\n Enter the elements of the first array");

for (i=0;i<n1;i++)

scanf("%d", &arr1[i]);

printf("\n Enter the number of elements in array 2: ");

scanf("%d", &n2);

printf("\n\n Enter the elements of the second array");

for (i=0;i<n2;i++)

scanf("%d", &arr2 [i]);

m = n1+ n2;

for(i=0;i<n1;i++)

{

arr3 [index] = arrl [i];

index++;

}

for (i=0;i<n2;i++)

{

arr3 [index] = arr2 [i];

index++;

}

printf("\n\n The merged array is");

for (i=0; i<m; i++)

printf("\t Arr [%d] = %d", i, arr3 [i]);

getch();

return 0;

}

Output

Enter the number of elements in array 1: 3

Enter the elements of the first array 10 20 30

Enter the number of elements in array array 2: 3

Enter the elements of the second array 15 25 35

The merged array is

Arr [0] = 10 Arr [1] = 15 Arr [2] = 30

Arr [3] = 15 Arr [4] = 25 Arr [5] = 35

If we have two sorted arrays and the resultant merged array also needs to be a sorted one, then the task of merging the arrays becomes a little difficult. The task of merging can be explained using Figure 5.17.

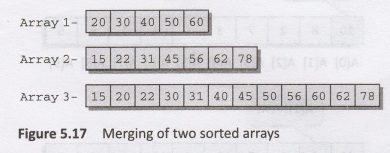
The figure shows how the merged array is formed using two sorted arrays. Here, we first compare the 1st element of array 1 with the 1st element of array 2, put the smaller element in the merged array. Since 20 > 15, we put 15 as the first element in the merged array. We then compare the 2nd element of the second array with the 1st element of the first array. Since 2022, now 20 is stored as the second element of the merged array. Next, 2nd element of the first array is compared with the 2nd element of the second array. Since 30 > 22, we store 22 as the third element of the merged array. Now, we will compare the 2nd element of the first array with 3rd element of the second array. As 30 < 31, we store 30 as the 4th element of the merged array. This procedure will be repeated until elements of both the arrays are placed in the right location in the merged array.

16. Write a program to merge two sorted arrays.

#include <stdio.h>

#include <conio.h>

int main()

{

int arr1 [10], arr2 [10], arr3 [20];

int i, nl, n2, m, index=0;

int index_first = 0, index_second = 0;

clrscr();

printf("\n Enter the number of elements in array1: ");

scanf("%d", &n1);

printf("\n\n Enter the elements of the first array");

for (i=0;i<n1; i++)

scanf("%d", &arr1 [i]);

printf("\n Enter the number of elements in array2: ");

scanf("%d", &n2);

printf("\n\n Enter the elements of the second array");

for (i=0;i<n2; i++)

scanf("%d", &arr2 [i]);

m = n1+n2;

while (index_first < n1 && index_second < n2)

{

if (arr1 [index_first] <arr2 [index_second])

{

arr3 [index] = arr1 [index_first];

index_first++;

}

else

{

arr3 [index] = arr2 [index_second];

index_second++;

}

index++;

}

/* if elements of the first array are over and the second array has some elements */

if (index first = = n1)

{

while (index second<n2)

{

arr3 [index] = arr2 [index_second];

index second++;

index++;

}

}

/* if elements of the second array are over and the first array has some elements */

else if (index_second = = n2)

{

while (index first <n1)

{

arr3 [index] = arr1 [index first];

index_first++;

index++;

}

}

printf("\n\n The contents of the merged array are");

for (i=0;i<m; i++)

printf("\n Arr [%d] = %d", i, arr3 [i]);

getch();

return 0;

}

Output

Enter the number of elements in array1: 3

Enter the elements of the first array 10 20 30

Enter the number of elements in array2: 3

Enter the elements of the second array 15 25 35

The contents of the merged array are

Arr [0] = 10 Arr [1] = 15 Arr [2] = 20

Arr [3] = 25 Arr [4] = 30 Arr [5] = 35

Searching for a Value in an Array

Searching means to find whether a particular value is pres- ent in the array or not. If the value is present in the array then searching is said to be successful and the searching process gives the location of that value in the array. Other- wise, if the value is not present in the array, the searching process displays the appropriate message and in this case searching is said to be unsuccessful.

There are two popular methods for searching the array elements. One is linear search and the second is binary search. The algorithm that should be used depends entirely on how the values are organized in the array. For example, if the elements of the array are arranged in ascending order, then binary search should be used as it is more efficient for sorted list in terms of complexity. We will discuss these two methods in detail in this section.

Linear Search

Linear search, also called sequential search, is a very simple method used for searching an array for a particular value. It works by comparing every element of the array one by one in sequence until a match is found. Linear search is mostly used to search an unordered list of elements (array in which data elements are not sorted). For example, if an array A [] is declared and initialized as

 int A[] = { 10, 8, 2, 7, 3, 4, 9, 1, 6, 5};

and the value to be searched is VAL = 7, then searching means to find whether the value 7' is present in the array or not. If yes, then the search is successful and it returns the position of occurrence of VAL. Here, POS 3 (index starting from 0). Figure 5.18 illustrates this concept.

Obviously, the best case of linear search is when VAL is equal to the first element of the array. In this case, only one comparison will be made.

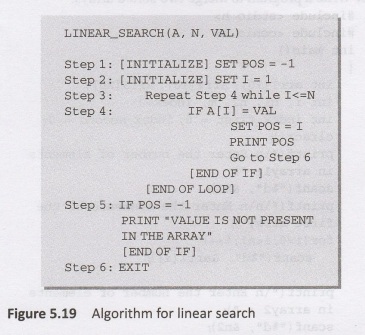
Likewise, the worst case will happen when either VAL is not present in the array or it is equal to the last element of the array. In both the cases, n comparisons will be made. However, the performance of the linear search algorithm (Figure 5.19) can be improved by using a sorted array.

In Step 1 and Sten 2 of the algorithm, we initialize the value of POS and I. Step 3, a while loop is executed that would be executed until I is less than N (total number of elements in the array). In Step 4, a check is made to see if a match is found between the current array element and VAL. If a match is found, then the position of the array element is printed else the value of I is incremented to match the next element with VAL. However, if all the array elements have been compared with VAL, and no match is found then it means that VAL is not present in the array.

17. Write a program to implement linear search.

#include <stdio.h>

#include <conio.h>

int main()

{

int arr [10], num, i, n, found= 0, pos = -1;

 clrscr();

printf("\n Enter the number of elements in the array : ");

scanf("%d", &n);

printf("\n Enter the elements:");

for (i=0; i<n;i++)

scanf("%d", &arr[i]);

printf("\n Enter the number that has to be searched : ");

scanf("%d", &num);

for (i=0;i<n;i++)

{

if (arr[i] = = num)

{

found =1;

pos=i;

printf("\n %d is found in the array at position = %d", num, i);

break;

}

}

if (found = = 0)

printf("\n %d does not exist in the array", num);

getch();

return 0;

}

Output

Enter the number of elements in the array:

5

Enter the elements: 1 2 3 4 5

Enter the number that has to be searched: 7

7 does not exist in the array

Binary Search

We have seen that the linear search algorithm is very slow. If we have an array with 1 million entries then to search a value from that array, we would need to make 1 million comparisons in the worst case. However, if the array is sorted, we have a better and efficient alternative known as binary search.

Binary search is a searching algorithm that works efficiently with a sorted list. The algorithm finds the position of a particular element in the array. The mechanism of binary search can be better understood by using the analogy of a telephone directory. When we are searching for a particular name in the directory, we will first open the directory from the middle and then decide whether to look for the name in the first part of the directory or in the second part of the directory. Again we will open some page in the middle and the whole process will be repeated until we finally find the name.

Now let us consider how this mechanism will be applied to search for a value in a sorted array. Given an array that is declared and initialized as

int A[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10); and the value to be searched is VAL = 9. The algorithm (Figure 5.20) will proceed in the following manner.

BEG = 0, END = 10, MID = (0 + 10)/2 = 5

Now, VAL = 9 and A [MID] = A[5] = 5

A [5] is less than VAL, therefore, we will now search for the value in the latter half of the array. So, we change the values of BEG and MID.

Now, BEG = MID + 1 = 6, END = 10, MID = (6 + 10)/2 =16/2 = 8

Now, VAL = 9 and A [MID] = A[8] = 8

A[8] is less than VAL, therefore, we will now search for the value in the latter half of the array. So, again we change the values of BEG and MID.dol mati)

Now, BEG = MID + 1 = 9, END = 10, MID = ( 9 + 10)/2 = 9

Now VAL 9 and A [MID] = 9.

In this algorithm we see that BEG and END are the beginning and ending positions of the segment that we are looking to search for the element. MID is calculated as (BEG + END) /2. Initially, BEG = lower _bound and END = upper_bound. The algorithm will terminate when A [MID] = VAL. When the algorithm ends, we will set POS = MID. POS is the position at which the value is present in the array.

However, if VAL is not equal to A [MID], then the values of BEG, END, and MID will be changed depending on whether VAL is smaller or greater than A [MID] .

(a) If VAL < A [MID], then VAL will be present in the left segment of the array. So, the value of END will be changed as, END = MID - 1

(b) If VAL A [MID], then VAL will be present in the right segment of the array. So, the value of BEG will be changed as, BEG = MID + 1

Finally, if VAL is not present in the array, then eventually END will be less than BEG. When this happens, the algorithm will terminate and the search will be unsuccessful. Figure 5.20 shows an algorithm for binary search.

In Step 1, we initialize the value of variables-BEG, END and POS. In Step 2, a while loop is executed until BEG is less than or equal to END. In Step 3, value of MID is calculated. In Step 4, we check if the value of A [MID] is equal to VAL (item to be searched in the array). If a match is found then value of POS is printed and the algorithm exits. However, if a match is not found and if the value of A [MID] is greater than VAL, then the value of END is modified otherwise if A [MID] is less than VAL, then value of BEG is altered. In Step 5, if the value of POS = -1, then it means VAL is not present in the array and an appropriate message is printed on the screen before the algorithm exits.

18. Write a program to implement binary search.

#include <stdio.h>

#include <conio.h>

Int main ( )

int arr [10], num, i, n, beg, end, mid,

found =0;

clrscr();

printf("\n Enter the number of elements in the array: ");

scanf("%d", &n);

printf("\n Enter the elements: ");

for (i=0;i<n;i++)

{

scanf("%d", &arr[i]);

}

printf("\n Enter the number that has to be searched: ");

scanf("%d", &num);

beg = 0, end = n-1;

while (beg ≤ end)

{

mid = (beg + end)/2;

if (arr [mid] = = num)

{

printf("\n %d is present in the array at position = %d", num, mid);

found=1;

break;

}

else if (arr [mid] >num)

end = mid-1;

else

beg = mid+1;

}

if (beg > end && found = = 0)

printf("\n %d does not exist in the array", num);

getch();

return 0;

}

Output

Enter the number of elements in the array: 5

Enter the elements: 1 2 3 4 5

Enter the number that has to be searched: 7

7 does not exist in the array