Normal Sub-groups and Cosets - Lagrange's Theorem

NORMAL SUB-GROUP AND COSETS - LAGRANGE'S THEOREM :

Definition 1: Left coset of H in G.

Let (H, *) be a subgroup of (G, *). For any a Є G, the set a H defined by

a H = {a * h/ h Є H} is called the left coset of H in G determined by the element a Є G.

The element a is called the representative element of the left coset a H.

Note: The left coset of H in G determined by a Є G is the same as the equivalence class [a] determined by the relation left coset modulo H.

Definition 2: Index of H in G [i_G (H)]

Let (H, *) be a subgroup of (G, *), then the number of different left (or right) cosets of H in G is called the index of H in G.

Definition 3. Normal sub-group

A subgroup (H, *) of (G, *) is called a normal sub-group if for any a Є G, a H = H a.

Definition 4. Quotient group (or) factor group :

Let N be a normal subgroup of a group (G, *).

The set of all right cosets of N in G be denoted by

G/N = {N_a |a Є G}

Definition 5. Direct product

Let (G, *) and (H, ∆) be two groups. The direct product of these two groups is the algebraic structure (G × H, o) in which the binary operation o on G × H is given by

(g₁, h₁) o (g₂, h₂) = (g₁ * g₂, h₁ o ∆ h₂)

for any (g₁, h₁), (g₂, h₂) Є G × H.

Definition 6. Group homomorphism :

Let (G, *) and (G', .) be two groups. A mapping f: G→ G' is called a group homomorphism if

∀ a, b Є G, f (a* b) = f (a) .f (b)

Definition 7. Kernel of group homomorphism :

Let (G, *) and (G', .) be two groups with e' as the identity element of G'

Let f: G→G' be a homomorphism.

ker f = {a Є G | f (a) = e'}

Statement 1: [Lagrange's theorem] [A.U A/M 2004, 2005, N/D 2004]

The order of a subgroup of a finite group divides the order of the group. (OR) If G is a finite group, then 0(H) | 0(G), for all sub-group H of G.

Statement 2: Fundamental theorem on homomorphism of groups

If f is a homomorphism of G onto G' with kernal k, then G/K ≈ G'.

Theorem 1:

Let (H, *) be a subgroup of (G, *). The set of left cosets of H in G form a partition of G. Every element of G belongs to one and only one left coset of H in G.

Proof: (i) To prove: Every element of G belongs to one and only one left coset of H in G.

Let H be a subgroup of a group G. Let a Є G. Then a H = H if and only if a Є H.

Proof: Let a Є G

a H = H = ae Є H = H⇒ a Є H

Conversely assume that a Є H

Then ah Є H, for all h Є H.

So a H ≤ H … (1)

Given any y Є H, a^-1 y Є H and y = a (a^-1 y) Є H.

So y Є a H for all y Є H.

(i.e.,) H ≤ a H

From (1) and (2) H = a H … (2)

Hence every element of G belongs to one and only one left coset of H in G.

(ii) To prove: The set of left cosets of H in G form a partition of G.

Let a, b Є G and H be a sub group of G.

If a H ∩ H a ≠ ф

Let c Є a H ∩ Н а

As c Є a H we have c H = a H

I. Let H be a subgroup of a group G. Let a, b Є G if  b Є a H, then b H = a H]

As c Є b H, we have c H = b H

So a H = c H = b H

Thus if a H ∩ b Ho, then a H =b H.

Therefore any two distinct left cosets are disjoint. Hence the set of all (distinct) left cosets of H in G forms a partition of G.

Theorem 2: [Lagrange's theorem]       [A.U A/M 2004, 2005, N/D 2004, 2010]

[A.U A/M 2011, June 2011, M/J 2012, M/J 2013, M/J 2014]

The order of a subgroup of a finite group divides the order of the group. (OR) If G is a finite group, then 0(H) | 0(G), for all sub-group H of G.

Solution Statement: If G is a finite group and H is a subgroup of G, then order of H is a divisor of order of G.

Proof :

Let 0(G) = n, (Here n is finite)

Let G = {a₁ = e, a₂, a₃, …, a_n} and let H be a subgroup of G

Consider the left cosets as follows

e * H = {e * h \ Є H}

a₂ * H = {a2 * H \ h Є H}

a_n * H = {a_n * h \ h Є H}

We know that any two left cosets are either identical or disjoint.

Also   0(e * H) = 0(H)

0(a_i *H) = 0(H), ∀ a_i Є G.

Otherwise if a * h_i = a * h_j for i ≠ j, by cancellation laws, we would have h_i = h_j, which is a contradiction.

Let there be k - disjoint cosets of H in K. Clearly their union equals G (i.e.,) G =

 (a₁ * H) U (a₂ * H) U … U (a_k * H)

0(G) = 0 (a₁* H) + 0 (a₂ * H) + … + 0(a_k * H)

= 0(H) + 0(H) + … +0(H)    → K-times

0(G) = K. 0(H)

This implies 0(H) is a divisor of 0(G).

Theorem 3: Let (G, *) and (H, ∆) be groups and g: G H be a homomorphism. Then the Kernel of g is a normal sub-group.    [A.U. N/D, 2004] [A.U A/M 2011, M/J 2012, M/J 2013]

Solution: Let K be the Kernel of the homomorphism g (i.e.,) K= {x Є G\g(x) e', where e' Є H is the identity element of H}

To prove that K is a subgroup:

Let x, y Є K, then g(x) = e' and g(y) = e'.

Claim: x * y^-1 Є K

By definition of homomorphism,

g (x *y^-1) = g (x) ∆  ́g ( y^-1) = g (x) ∆ [g (y) ]^-1

= e' A (e')^-1

= e' A e' = e'.

Hence x * y-1 Є K and this proves K is a sub-group of G by a criterion for sub-groups.

To prove that K is normal: Let x ЄK, f Є G, then g(x) =e'

Claim : f * x * f^-1 Є K

g (f * x *ƒ^-1) = g(f) + g(x) = g (f^-1)

= g(f).e^-1 [g(f)]^-1

= g(f) [g(f)^-1]

= e'

f * x * f^-1 Є K.

Thus K is a normal subgroup of G.

Theorem 4: (Fundamental Thereom on homomorphism of groups) If f is a homomorphism of G onto G' with kernal K, then G/KG'.    [A.U June 2011, N/D 2013]

Proof :

Let f : G→G' be a homomorphism from the group (G, *) to the group (G', A).

Then K Ker (f) = {x Є G | f(x) = e'} is a normal sub-group of (G, *)

ϕ (K a) = f (a), for any a Є G

Since, if K_a = K_b

⇒  a * b^-1 Є K

⇒ ƒ (a * b^-1) = e'

f (a) ∆ f (b) = e'

f (a) ∆ [f (b)^-1] = e'

f (a) ∆ [f (b)^-1 ∆ [f (b)] = e' ∆ f (b)

⇒ f (a) ∆ e' = f (b)

⇒ f (a) = f (b)

⇒ ϕ (Ka) = ϕ (Kb)

ϕ is well defined.

Claim: ϕ is a homomorphism.

Let Ka, K b Є G/K

Now ϕ (Ka o Kb) = ϕ [K (a + b)]

= f [(a * b)]

= f (a) ∆ f (b)

= ϕ (Ka) ∆ (K b)

ϕ is a homomorphism.

Claim: ϕ is one-to-one.

If ϕ (Ka) = ϕ (K b)

then f (a) = f (b)

f (a) ∆ f (b) = f(b) ∆ ƒ(b^-1)

f (a * b^-1) = f (b * b^-1) = f(e) = e'

a * b^-1 Є K ⇒ Ka = K b

ϕ is one-to-one.

Claim: ϕ is onto.

Let y be any element of G'.

Since f: G→G' is a homomorphism from G onto G', therefore there exists an element a Є G such that f(a) = y

For every a Є G, K a Є G/K

We get ø (K a) = f(a), for all f(a) = y Є G'

ϕ is onto.

ϕ : G/K → G' is an isomorphism.

ϕ : G/K = G'

Theorem 5: Prove that the intersection of two normal subgroups is a normal subgroup.      [MCA May, 91, MU] [A.U M/J 2013]

Solution: Let H and K be any two normal subgroups of a group G. We have to prove that H∩K is normal in G.

Since H and K are subgroups of G, e Є H and e Є K.

Hence e Є H∩K. Thus H ∩ K is a non-empty set.

Let a, b Є H∩K

Claim: ab^-1 Є H∩K

Since, a, b Є H∩K, both a, b being to H and K.

Since H and K are subgroups of G, ab^-1 Є H and ab^-1 Є K

so that ab^-1 Є H∩K.

Hence H∩K is a subgroup of G, by a criterion for subgroup.

To prove: H∩K is normal:

Let x Є H∩K, and let g Є H

Since x Є H∩K and x Є H and x Є K

Since x Є H, g Є G, ⇒ g x g^-1 Є K (as H is normal)

Likewise x Є K, g Є G Є ⇒ g x g^-1 Є K (as K is normal)

Hence x Є H∩K and g Є G ⇒ g x g^-1 Є H∩K

This H∩K is a normal subgroup of G.

Theorem 6: Every subgroup of an abelian group is a normal subgroup. [A.U N/M 2013]

Proof: Let (G, *) be an abelian group and (N, *) be a subgroup

Let g be any element in G and let n Є N.

Now, g * n * g^-1 = (n * g) * g^-1     [ G is abelian]

= n (g * g^-1)

= n * e

= n Є N

∀ A g Є G and n Є N, g * n * g^-1 Є Ν

(N, *) is a normal subgroup.

Theorem 7: Let < H, *> be a subgroup of < G, *>. Then show that < H, *> is a normal subgroup iff a * h * a^-1 = H, ∀ a Є G.   [MCA, Nov., 93, May 92, MU]

Solution: Let H be normal in G.

Then by definition a* H = H * a, for all a Є G.

Then a * H * a⁻¹ = a* (a^-1 * H)

 = (a * a^-1) * H

= e * H

= H

Conversely let a^-1 * H * a = H, for all a Є G.

(i.e.,) a * (a^-1 * H * a) = a * H)

(i.e.,) (a * a^-1) * (H * a) = a * H

(i.e.,) e* (H * a) = a * H

(i.e.,) H * a = a * H

Thus H is a normal subgroup.

Theorem 8: Let < A, * > be a group. Let H = {a/a Є G and a * b = b * a ∀ b Є G}. Show that H is a normal subgroup.  [MCA May, 1990, March, 96, MU]

Solution: H = {a Є G | a * b = b * a, ∀ b Є G}.

Since e*a = a*e = a, ∀ a Є G, we have e Є H.

H is non-empty

Let x, y Є H. Then

a*x = x*a, ∀ x Є G and a*y = y*a, ∀ y Є G.

Claim: H is a normal subgroup.

Consider a* (x * y) = (a *x) *y

= (x*a) *y

= x* (a* y)

= x* (y * a)

= (x * y) *a

⇒ x * y Є H.

Let a Є H then a * x = x * a, ∀ x Є G

then a^-1 * (a*x) = a^-1 * (x * a)

⇒ x = a ^-1 + (x *a)

⇒ x * a^-1 = a^-1 * (x * a) * a^-1

= (a^-1 * x) * (a * a^-1)

= a^-1 * x

⇒ x * a^-1 = a^-1 * x, ∀ x Є G

⇒ a^-1 Є Н

Thus H is a sub-group.

To prove :

H is normal

Let x Є H, g Є G

Then a *x = x*a, ∀ a Є G

Then g*x*g^-1 = x*g*g^-1

⇒ x Є H

Thus    g*x*g^-1 Є H ⇒ H is normal.

Theorem 9 : N is a normal subgroup of G if and only if g N g^-1 = N for every g Є G (or g N = N g)

(OR)

Show that the number of right and left cosets are equal in normal subgroups, and every left coset is a right coset.

Proof :

Let N be a normal subgroup of G.

Let x Є g N g^-1 ⇒ x = gng^-1, for some n Є N

x = gng^-1 Є Ν ( N is a subgroup normal)

g N g^-1 ≤ N.

Now, g^-1 N g = g^-1 N (g^-1)^-1 ≤ N

since g^-1 Є G, and g^-1n g Є N

N = g (g^-1 Ng) g^-1 Є g N g^-1

N ≤ g N g^-1

Therefore, N = g Ng^-1

Conversely,

Let g N g^-1 = N, for every g Є G.

We mean g N g^-1 is set of all gng^-1, for n Є N.

Clearly g N g^-1 ≤ N

N is a normal subgroup.

We get, if N is a normal subgroup then g N g^-1 = N (or) g N = N g that is the left and right cosets are equal.

Therefore the number of right and left cosets are equal in normal subgroups, and every left coset is a right coset.

Theorem 10: Let f: G → G' be a homomorphism, then the Ker (f) is a normal subgroup of G.

Solution: We know that Ker (f) {x Є G | f(x) = e'} is a ( subgroup of (G, *)

Now we can prove that ker (f) is a normal subgroup of G.

Let g Є G and n Є = ker (f).

Now ƒ (g* n*g^-1) = ƒ (g) ∆ ƒ (n) ∆ ƒ(g^-1)

= f(g) ∆ e' ∆ f(g^-1)

= f(g) ∆ fg^-1)

= ƒ (g*g^-1) = ƒ (e)

= e'

(g*n*g^-1) Є Ker (f)

(Ker (f), *) is a normal subgroup of (G,. *).

Thereom 11: The direct product of the two groups is a group.

Solution: Let (G₁, *₁) and (G₂, *₂) be two groups. Their direct product is the structure (G₁, G₂, *) in which the binary operation * is defined by (a₁, b₁) * (a₂, b₂) = (a₁ *₁a₂, b₁ *₂ b₂).

Then G₁ × G₂ is a group.

Proof :

(i) Associative of *

Let a, b, c Є G₁ × G₂ and a = (x₁, y₁) b = (x₂, y₂), c = (x₃, y₃) for some x₁, x₂, x₃ Є G₁ and y₁, y₂, y₃ Є G₂.

Now

a * (b*c) = (x₁, y₁) * ((x₂ * y₂) * (x₃, y₃))

= (x₁, y₁) * (x₂ *₁ x₃, y₂ *₂ y₃) by definition of *

= (x₁ *₁ (x₂ *₁ x₃), y₁ *₂ (y₂ *₂ y₃))   by definition of *

= (x₁ *₁ x₂ ) *₁ x₃, (y₁ *₂ y₂ ) *₂ y₃))   by associative law for *1, *2

= (x₁ *₁ x₂, y₁ *₂ y₂ ) * (x₃, y₃))  

= (x₁, y₁) * (x₂, y₂ ) * (x₃, y₃))  

= (a*b) *c

So associative axiom is satisfied in G for *.

(ii) Identity for *.

As we can expect, if e₁ and e₂ are identities for G₁ and G₂ respectively, then e = (e₁, e₂) is the identity for G₁ x G₂.

Let a = (x₁, y₁) Є G₁ x G₂

a *e = (x₁, y₁) * (e₁, e₂)

= (x₁*₁ e₁, y₁ *₂ e₂)

= (x₁, y₁) = a

Similarly, e*a = a

So a*e = e*a = a

Hence e = (e₁, e₂) is the identity element in G.

(iii) Inverse in G₁ × G₂.

The inverse of an element e in G1 × G2 is determined compotent wise.

(i.e.,) a' = (x₁, y₁) ' = (x₁', y₁')

This can be verified as follows :

= (x₁, y₁) (x₁', y₁')

= (x₁ *₁ x₁', y₁ *₂ y₁') by definition of *

= (e₁, e₂) = e.

Similarly a' *a = (e₁, e₂) = e

So, (x₁, y₁)' = (x₁',y₁')

From (i), (ii) and (iii) it follow that G = G₁ × G₂ is a group.

Theorem 12: Every group of prime order is cyclic (and hence abelian).

Solution :

Let G be a group with O (G) = P, a prime.

Let a≠e Є G and H = <a> be the cyclic subgroup of G generated by a.

By Lagrange's theorem. O (H) | p. So O (H) = 1 or p.

Since O (H) ≠ 1, (as a≠ e and a, e Є H, O(H) ≥ 2), we have O (H) = p.

So G = H<a>, a cyclic group, (as every cyclic group is a abelian, G is abelian).

Example 1: Let G = {1, a, a², a³} (a⁴ = 1), be a group and H = {1, a²} is a subgroup of G under multiplication. Find all the cosets of H.

Solution:

Let us find the right cosets of H in G.

H1 = {1, a₂} = H

Ha = {a, a³}

H a² = {a², a⁴] = {a², 1} = H

and H a³ = {a³, a⁵} = {a³, a} = Ha

H.1 = H = Ha² = {1, a²} and Ha = Ha³ = {a, a³}

are two distinct right cosets of H in G. Similarly, we can find the left cosets of H in G.

Example 2: Find the left cosets of {[0], [2]} in the group (Z₄, +₄).

Solution :

Let Z₄ = {[0], [1], [2], [3]} be a group and H= {[0], [2]} be a sub-group of Z₄ under +₄ (addition mod 4).

The left cosets of H are

[0] + H = {[0], [2]} = H;

[1] + H = {[1], [3]} ;

[2] + H = {[2], [4]} = {[2], [0]} = {[0], [2]} = H

and [3] + H = {[3], [5]} = {[3], [1]} = {[1], [3]} = [1] + H.

[0] + H = [2] + H = H and [1] + H = [3] + H

are the two distinct left cosets of H in Z₄.

Example 3: Let (G, *) be a group of order 2 in which G = {e, a}. Find the direct product of (G, *) with itself.

Solution :

The composition table of (G, *) is

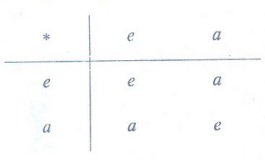
From this composition table, we can easily write the direct product. The direct product of G with itself is (G x G, o) where o is defined by (a₁, b₁) o (a₂, b₂) = (a₁ * a₂) (b₁ * b₂) for any (a₁, b₁) (a₂, b₂) Є G × G.

G = {e, a}

G ˟ G = {(e, e), (e, a), (a, e), (a, a)}

The Cayley's table for o is given below:

Example 4 Let G be a group and a Є G The map f: G → G defined by f (x) = axa^-1 for all x Є G, is an isomorphism.    [A.U N/D 2010]

Solution :

The map ƒ is a homomorphism if x, y Є G, then

f (x) f (y) = (axa^-1) (aya^-1)

= ax (a^-1a) ya^-1

= axya^-1

= a (xy) a^-1

= f (xy).

So f is a homomorphism.

f is one-to-one : If f (x) = f(y), then axa^-1 = aya^-1 so by left cancellation, we have xa^-1 = ya^-1, again by right cancellation we get x = y.

f is onto : Let y Є G, then a^-1 ya Є G and f (a^-1 ya)

= a (a^-1 ya) a^-1

= (aa^-1) y (aa^-1)

= y.   So f (x) = y for some x Є G.

Thus f is an isomorphism.

Example 5: Any two infinite cyclic groups are isomorphic to each other.

Solution :

Let G₁ = <a> and G₂ = <b> be two cyclic group of infinite order.

G₁ = {aⁿ | is an integer} and G₂ {bⁿ | is an integer}.

Define a map f: G₁ → G₂ by f (aⁿ) = bⁿ

Let x, y Є G₁, then x=aⁿ, y=a^m for some integers n and m.

f(x) f(y) = f (aⁿ) .ƒ (a^m) = bⁿ b^m = b^n+m = f (a^n+m)

= ƒ (aⁿ a^m) = f(xy).

So f is a homomorphism.

If f(x) = f(y), then ƒ (aⁿ) ƒ (a^m), (i.e.,) bⁿ = b^m.

Then b^n-m = e' in G₂. As G₂ is an infinite cyclic group generated by, there is no non-zero integer k such that b^k = e'. Hence from b^{n- m} = e', we have n-m = 0, (i.e.,) n = m and x= aⁿ = a^m = y. Thus f is one-to-one.

Let z Є G₂. Then z=bⁿ for some integer n. Now take x = aⁿ.

Then f(x) = f (aⁿ) = bⁿ = z. So the map ƒ is onto.

Then f is one-to-one, onto homomorphism. (i.e.,) it is an isomorphism.

Example 6: Determine all the proper subgroups of the symmetric group (S_S, ◊) described in table.

Solution: From the table it is clear that {P₁, P₂}, {P₁, P₃}, {P₁,P₄} and {P₁, P₅, P₆} are subgroups of (S_S, ◊). The left cosets of {P₁, P₂} are {P₁, P₂}, {P₃, P₆}, and {P₄, P₅}, while the right cosets of {P₁, P₂} are (P₁, P₂}, {P₃, P₅} and {P₄, P₆}. Hence (P₁, P₂} is not a normal subgroup.

Similarly, we can show that {P₁, P₃} and {P₁, P₄} are also not normal subgroups. On the other hand, the left and right cosets of {P₁, P₅, P₆} are {P₁, P₅, P₆} and {P₂, P₃, P₄}. Hence {P₁, P₅, P₆} is a normal subgroup.

Example 7: How many generators are there in a cyclic group of order 10?

Solution:

We have a is the generator then am is also generator if and only if

(m, n) = 1

Now, we have

(1, 10) = 1

(3, 10) = 1

(7, 10) = 1

(9, 10) = 1 (and (2, 10) = 2 (5, 10) = 5 ...)

There are 4 generators, which are a, a³, a⁷, a⁹ whenever a is a generator.