Normal Forms

NORMAL FORMS

-Principal conjunctive and disjunctive normal forms

Normal forms

By constructing and comparing truth tables we can determine whether two statement formulas A and B are equivalent. But this method is very tedious and difficult to solve even on a computer because the number of entries increases very rapidly as n increases.

A better method is to transform the statement formulas A and B to some standard forms A's and B' such that a simple comparison of A and B shows whether A ⇔ B.

The standard forms are called canonical forms or normal forms.

Let A (P₁, P₂, … P_n) be a statement formula where P₁, P₂, ... P_n are the primitive variables. If A has the truth value T for atleast one combination of truth values assigned to P₁, P₂, … P_n then A is said to be staisfiable. The process of determining, in a finite number of steps, whether a given statement formula is a tautology or a contradiction or atleast satisfiable is known as a decision problem. But decision problem of a formula which involves more number of variables is quite different, even with the help of a computer. Therefore we are in need of other procedures known as reduction to normal forms.

Note: It will be convenient to use the word "product" in place of "conjunction" and "sum" in place of "disjunction".

Definition: Elementary product

A product of the variables and their negations in a formula is called an elementary product. (product means conjunction).

Example: Let P and Q be any two atomic variables. Then P, ┐P^Q, ┐Q^P, P^┐P and Q^┐P are elementary products.

Definition: Elementary sum

A sum of the variables and their negations in a formula is called an elementary sum. (Sum means disjunction).

Example: Let P and Q be any two variables. Then P, ┐PVQ, ┐QVP, PV┐P and QV┐P are elementary sums.

Definition: Factor

Any part of an elementary product or elementary sum, which is itself an elementary product of sum is a factor of the product or sum.

Example: Q v P is a factor of ┐QvQVP

Note 1: An elementary product is identically false if it contains atleast one pair of factors in which one is negation of the other.

Example: P^┐P ↔ F

Note 2: An elementary sum is identically true if it contains atleast one pair of factors in which one is negation of the other.

Example: Pv┐P ↔T.

Disjunctive Normal Form (DNF)

Definition

A formula which is equivalent to a given formula and which consists of a sum of elementary products is called a disjunctive normal form (DNF) of the given formula.

Procedure to obtain DNF

1. An equivalent formula can be obtained by replacing → and ↔ with ^, V and ┐.

2. Apply negation to the formula or to a part of the formula and not to the variables.

3. Using DeMorgan's law, apply negation to variables.

4. Repeated application of distributive laws will give the required DNF.

Remark :

1. A given formula may not have unique DNF. We may get different DNF's if we apply distributive law in different ways.

2. A given formula is false if every elementary product in DNF is identically false.

Example 1: Obtain disjunctive normal forms of P ^ (P → Q)"

Solution Let S ↔ P^(P→Q)

↔  P ^ (┐PVQ)  [ P→Q ↔ ┐PVQ]

↔ (P^┐P) V (PɅQ)

[by distributive law]

Example 2: Obtain disjunctive normal forms of ┐(PVQ) ↔  PɅQ.

Solution: Let S ↔  ┐(PVQ) ↔  PɅQ

↔ [┐(PVQ)^(PɅQ)] V [┐┐(PVQ)^( ┐P^Q)]

[ R↔S↔ (RɅS) V (┐RɅ┐S)}

↔ [┐ (PVQ) Ʌ (PɅQ)] V [(PVQ) Ʌ ┐(P Ʌ Q)] [ by negation law]

↔ [(┐P ^ ┐Q) ^ (P^Q)] v [(P v Q) ^ (┐P v ┐Q)] [ by DeMorgan's law]

↔ [┐P Ʌ ┐Q) ^ (P^Q)] v [[(P v Q) ^ ┐P] v [(P v Q) ^ ┐Q)] ['. by distributive law]

↔ [(┐P^7Q) ^ (P^Q)] v [[(P^┐P) v Q^┐P)] V (PɅ┐Q) V (QɅ┐Q)]] [ by distributive law]

↔ [(┐P Ʌ ┐Q) Ʌ (P^Q)] V (P Ʌ ┐P) v (Q Ʌ ┐P) V (P Ʌ ┐Q) V(Q ^ ┐Q)

Example 3: Obtain a disjunctive normal form of P→ ((P→ Q) ^ ┐ (┐QV ┐P))

Solution :

Let $  ⇔ P→ ((P→ Q) ^ ┐ (┐Q V ┐P))

↔ ┐P v ((P→ Q) ^ ┐ (┐Q V ┐P))

['.' (P→Q) ⇔  (┐PVQ)]

↔ ┐P V [(┐PVQ) ^ (Q^P)]

['.' (P→Q) ⇔ (┐PVQ) and Demorgan's law]

↔ ┐P V [(┐P ^ (Q^P)) v (Q ^ (Q ^ P))]  ['.' Distributive law]

↔ ┐P V (┐P ^ (Q ^ P)] v [Q ^ (Q^P)]

↔ ┐P V [┐P ^ (Q ^ P)] V [Q^Q) ^ P]  ['.' Associative law]

↔ ┐P V [┐P ^ (Q ^ P)] V [Q^P] 

['.' Q^Q ⇔ Q]

Example 4: Obtain a disjunctive normal form of

PɅ┐(Q V R)) V (((P Ʌ Q) v ┐R) ^ P)

Solution: PɅ┐(Q V R)) V (((P Ʌ Q) v ┐R) ^ P) Reasons

↔ (P^ (┐Q ^ ┐R)) v (((P^Q)V ┐R)^P) De Morgan's law

↔ (P^┐Q ^ ┐R)) v ((P^Q) ^P) V (┐R^P) Distributive law

↔ (P^ ┐Q ^ ┐R) v ((P^ (Q^P)) V (┐R^P)) Associative law

↔ (P^ ┐Q ^ ┐R) v ((P^ (P^Q)) V (┐R^P)) Commutative law

↔ (P^ ┐Q ^ ┐R) v ((P^ P)^Q)) V (┐R^P)) Associative law

↔ (P^ ┐Q ^ ┐R) v (P^Q) V (┐R^P) Idempotent laws

This is the required DNF, as it is a sum of elementary products.

Example 5: Obtain a disjunctive normal form of (Q V (P ^ R)) ^ ((PVR) Ʌ Q) [A.U N/D 2012]

Solution: (Q V (P ^ R)) ^ ((┐PVR) Ʌ 'Q) Reason

↔ (Q v (P^R)) ^ ((┐PVR) v ┐Q) De Morgan law

↔ (Q v(P^R)) ^ ((┐P ^ ┐R) v ┐Q) De Morgan law

↔ (Q ^ (┐P ^ ┐R)) v (Q ^ ┐Q) v ((P ^ R) ^ ┐P ^ ┐R) v ((P ^ R) Ʌ ┐Q) extended distributive law

↔ (┐P ^ Q ^ ┐R) v F V (F ^ R) V (P ^ ┐Q ^ R) Negation law

↔ (┐р ^ Q ^ ┐R) V (P ^ ┐Q^R) Domination law

This is the required DNF, as it is a sum of elementary products.

Example 6: Obtain the DNF for (P→(Q^R))^(( ┐P→7 Q)^ ┐R)) [A.U N/D, 2003]

Solution :

P→(Q^R))^(( ┐P→ ┐Q)^ ┐R) Reasons

↔ (┐P v(Q^R))^(( P v ┐Q) ^ ┐R) De Morgan and Double negation

↔ (┐P v(Q^R))^(( P ^ ┐R) v(┐Q ^ ┐R) Distributive law

↔ (┐P ^ (P ^ ┐R)) V (┐P ^ (┐Q ^ ┐R)) v ((Q^R) ^ (P ^ ┐R)) V ((Q^R) ^ (┐Q ^ ┐R)) extended distributive law

((┐P^P) ^ ┐R) V (┐P^ (┐Q ^ ┐R)) V ((Q ^ R) ^ (P ^ ┐R)) V ((Q^R) ^ (┐Q^┐R)) Associative law.

 ↔ (F ^ ┐R) v (┐P ^ (┐Q ^ ┐R)) V ((Q ^ R) ^ (P ^ ┐R)) V ((Q^R) ^ (┐Q^┐R)) Negation law

↔ (F v (┐P ^ (┐Q ^ ┐R)) V ((Q ^ R) ^ (P ^ ┐R)) V ((Q ^ R) ^ (┐Q ^ ┐R)) Domination law

↔ (┐P ^ (┐Q ^ ┐R)) V ((Q ^ R) ^ (P ^ ┐R)) V ((Q ^ R) ^ (┐Q ^ ┐R)) Identity law

This is the required DNF, as it is a sum of elementary products.

Example 7: Obtain the disjunctive normal form of

(┐P v ┐Q) → (┐P ^ R).

Solution: (┐P v ┐Q) → (┐P ^ R)   Reasons

↔ (┐P v ┐Q) v (┐P ^ R)    since P→ Q ↔ ┐P V Q

↔ (P ^ Q) v (┐P ^ R)   De Morgan law

which is the required DNF

Example 8: Obtain the disjunctive normal form of

(┐P→ ┐Q) v (P↓ Q)

Solution (┐P→ ┐Q) v (P↓ Q)   Reasons

↔ (P v ┐Q) v (P v Q)    (P → Q) ↔ ┐P v Q

                                         (P↓ Q) ↔ ┐ (P v Q)

↔ ┐ (┐P ^ Q) v (┐P ^ ┐Q)   De Morgan law

which is the required DNF.

Conjunctive Normal Form :

A formula. which is equivalent to a given formula and which consists of a product of elementary sums is called a conjunctive normal form of the given formula.

Remarks:

(1) Again CNF is not unique for a formula.

 (2) A given formula is identically true if every elementary sum in CNF is identically true.

Example 1: Obtain a conjunctive normal form of P Ʌ (P→Q).

Solution : P Ʌ (P→Q)    Reason

↔ P Ʌ ( ┐P v Q)   

which is in CNF as P, ┐P v Q are elementary sums.

Example 2: Obtain a conjunctive normal form of  ┐ (PVQ) ↔ (P^Q).

Solution: ┐(P v Q) ↔ (P Ʌ Q)   Reasons

↔ (┐(P v Q) → (P Ʌ Q)) Ʌ ((P Ʌ Q) → ┐(P v Q))     R ↔ S ↔ (R→ S) ^ (S→R)

↔ (P V Q) V (P Ʌ Q) Ʌ ┐ (P ^ Q) v ┐(P V Q)      R→S ↔ ┐RVS

↔ P v Q v (P ^ Q) ^ (┐P v ┐Q v (┐ P ^ ┐Q))  De Morgan's law

↔ (P v Q v P) ^ (P v Q v Q) ^ (┐P v ┐Q v ┐P) ^ (┐P v ┐Q v ┐Q) using distributive law

This is the required CNF, as each of P v Q v P, ┐P v ┐Q v ┐P, ┐P v ┐Q v ┐Q is an elementary sum.

Example 3: Obtain a CNF for Q V (P Ʌ ┐Q) V (┐P ^ ┐Q)

Solution :

Q V (P Ʌ ┐Q) V (┐P Ʌ ┐Q)          Reasons

↔ (Q V ((P V ┐P)   ┐Q)       (P Ʌ ┐Q) V (┐P ^ ┐Q) ↔ (P V ┐P) Ʌ ┐Q)   distributive law

↔ (Q V (P V ┐P)) Ʌ (Q v ┐Q)    distributive law

↔ (Q V (P V ┐P) Ʌ (Q v ┐Q)

This is a CNF, as Q V P V ┐P, Q v ┐Q are elementary sums.

Example 4: Obtain a CNF for (P → (Q^R)) ^ (┐P → ┐Q ^ ┐R))  [A.U N/D 2003]

Solution : (P→(Q^R)) ^ (┐P → ┐Q ^ ┐R))     Reasons

↔ (┐P v (Q^R)) ^ (P v (┐Q ^ ┐R))     P→R ↔ ┐PVR

↔ ((┐P v Q)^( ┐PVR))^((P v ┐Q)^(P V┐R))     distributive law

This is a CNF, as it is a product of elementary sums.

Example 5: Obtain a conjunctive normal form of the formula.

P → ((P →Q) ^ ┐(┐Q v ┐P))  [A.U N/D 2003]

Solution :

P → ((P → Q) ^ ┐ (┐Q v ┐P))   Reasons

↔ ┐P v ((P → Q) ^ ┐(┐Q v ┐P))    P→R ↔ ┐PVR

↔ ┐P v ((┐P v Q) ^ ┐(┐Q v ┐P))    P→R ↔ ┐PVR

↔ ┐P v ((┐P v Q) ^ (Q ^ P))    De Morgan's law  

↔ (┐P v (┐P v Q)) ^ ((┐P  v (Q ^ P)))     Distributive law

↔ ((┐P v ┐P ) v Q) ^ ((┐P  v Q )^ (┐P v P))    associative law

↔ (┐P v Q) ^ (┐P v Q) ^ T      Negation law

↔ (┐P v Q) ^ (┐P v Q)        identity law

This is a CNF, as it is a product of elementary sums.

Example 6: Find a conjunctive normal of (Q V (P Ʌ R)) ^ ┐ ((P v R) ^ Q)

Solution :

(Q V (P Ʌ R)) ^ ┐ ((P v R) ^ Q)   Reasons

↔ (Q V (P Ʌ R)) ^  (┐(P v R) v ┐Q)     De Morgan's law

↔ (Q V (P Ʌ R)) ^  ((┐(P Ʌ ┐R) v ┐Q)     De Morgan's law

↔ (Q V P) Ʌ (Q v R) ^ (┐P v ┐Q) ^  (┐R v ┐Q)     Distributive law

Example 7: Show that the formula Q Ʌ (P Ʌ ┐Q)  V (┐P Ʌ ┐Q) is a tautology, by obtaining a conjunctive normal form, of the formula :

Solution: We first obtain a CNF of the given formula

Q Ʌ (P Ʌ ┐Q) V (┐P Ʌ ┐Q)

Q v ((P v ┐P) Ʌ ┐Q using the distributive law

(Q v (P v ┐P)) ^ (Q v ┐Q) again by distributive law

(Q v P v ┐P) ^ (Q v ┐Q)

This is a CNF, as Q v P V ┐P, Q V ┐Q are elementary sums.

A CNF is identically true (i.e.,) a tautology.

Min terms

Let P and Q be two statement variables. Construct all possible formula which consist of conjunctions of P or its negation and conjuctions of Q or its negation. None of the formula should contain both a variable and its negation. Delete a formula if it is the commutative of any one of the remaining formulae. Such conjunctions of P and Q are called the min terms of P and Q.

Example :

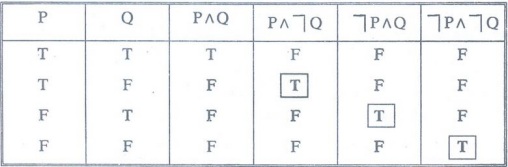
Minterms of P and Q are PɅQ, PɅ┐Q, ┐PɅQ and ┐PɅ┐Q

Note:

(i) PɅQ or QɅP is included but not both.

(ii) PɅ┐P and QɅ┐Q are not allowed.

(iii) No two minterms are equivalent.

(iv) Each minterm has the truth value T for exactly one combination of the truth values of the variables P and Q.

Minterms of P and Q.

Note :

1. No two minterms are equivalent.

2. Minterms for three variables P, Q, R are

P^Q^R, P^Q^┐R, P^┐Q^R, P^┐Q^┐R, ┐р^Q^R, ┐P^Q^┐R, ┐P^┐Q^R, ┐P^┐Q^┐R .

For a given formula an equivalent formula consisting of disjunctions of minterms only is known as its principal disjunctive normal form or the sum of products normal form.

3. In general for given n-number of variables there will be 2ⁿ minterms.

Principal Disjunctive Normal Form (PDNF)

The sum of products normal form

A formula which is equivalent to a given formula and which consists of sum of its min terms is called "principal disjunctive normal form" (or) "sum of product of canonical form" of the given formula. Construction of PDNF without truth tables:

(i) to replace conditionals and biconditionals by their equivalent formula involving Ʌ, V, ┐only.

(ii) to use De Morgan's laws and distributive laws.

(iii) to drop any elementary product which is a contradiction.

(iv) to obtain minterms in the disjunctions by introducing missing factors.

(v) to delete identical minterms keeping only one, that appear in the disjunctions.

Maxterms

For a given number of variables, the maxterm consists of disjunctions in which each variable or its negation, but not both, appears only once.

Remarks:

(i) The max terms are the duals of minterms.

(ii) Either from the duality principle or directly from the truth tables, it can be ascertained that each of the maxterms has the truth value F for exactly one combination of the truth values of the variables.

(iii) Different maxterms have the truth value F for different combinations of the truth values of the variables.

Maxterms of P and Q.

Principal Conjunctive Normal Form (or) Product - of - sums canonical form :

An equivalent formula consisting of conjunctions of max terms only is known as its principal conjunctive normal form or the product-of-sums canonical form.

Remark :

Every formula which is not a tautology has an equivalent PCNF which is unique except for the rearrangement of the factors in the maxterms as well as in the conjunctions.

Note: 1. To find pcnf from the pdnf

S ↔ (PɅQ) V (┐PɅQ) (pdnf)

(i) Write negation S that is nothing but the disjunction of the remaining minterms.

The minterms of P and Q are

P^Q, P^┐Q, ┐P^Q, ┐P^┐Q

Given : P^Q, ┐P^Q

Remaining term: P^┐Q, ┐P^┐Q

┐S ↔ (P^┐Q) V (┐P^┐Q)

(ii) Negation of the disjunctive normal form ┐S apply duality principle.

┐(┐S) ↔ (┐PvQ) Ʌ (PVQ)

S ↔ (┐PvQ) Ʌ (PVQ) (pcnf)

Note 2. To find pdnf from the pcnf.

S ↔ (PvQ) Ʌ (┐PVQ) (pcnf)

(i) Write the negation S that is nothing but the conjunction of the remaining maxterms.

The maxterms of P and Q are

PVQ, ┐PVQ, PV┐Q, ┐PV┐Q

Given: PVQ, ┐PVQ

Remaining terms: PV┐Q, ┐PV┐Q

┐S ↔ (PV┐Q) Ʌ (┐PV┐Q)

 (ii) Negation of the conjunctive normal form by using duality principle.

┐ (┐S) ↔ (┐P Ʌ Q) V (P Ʌ Q) (pdnf)

S ↔ (┐P Ʌ Q) V (P Ʌ Q) (pdnf)

Note 3 : S ↔ (P^Q) V (┐P^Q) V (┐P^┐Q) V (P^┐Q)

┐S ↔ There is no remaining minterms

Pcnf ↔ no pcnf for the given formula.

Note 4 : S ↔ (P V Q) Ʌ (┐P V Q) Ʌ (┐P V ┐Q) Ʌ (P V ┐Q)

┐S ↔ There is no remaining maxterms

Pdnf ↔ no pdnf for the given formula.

Example 1. Obtain the principal disjunctive normal form of

┐PVQ (or) P→ Q. Also find p.c.n.f

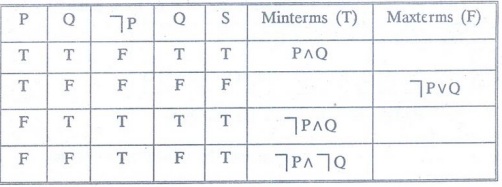
Solution: Let S ↔ ┐PVQ

Method 1. Truth table method

S ↔ (P^Q) V (┐P^Q) V (┐P^┐Q)     [(p.d.n.f) = disjunctions of minterms]

S ↔ ┐PVQ         [p.c.n.f = conjunction of maxterms]

Method 2:

Let S ↔ ┐PVQ

↔ (┐P Ʌ T) V (Q Ʌ T)       PɅT ↔ P, ┐PɅT ↔ ┐P, QɅT ↔ Q

↔ [┐P Ʌ (Q V ┐Q)] V [Q Ʌ (P V ┐P)]      QV┐Q ↔ T, PV┐P ↔ T

↔ [(┐PɅQ) V (┐PɅ┐Q)] V [(QɅP) V (QɅ┐P)]    distributive law.

↔ (┐PɅQ) V (┐PɅ┐Q) V (QɅP) V (QɅ┐P)

↔ (┐PɅQ) V (┐PɅ┐Q) V (QɅP)       ┐PɅQ ↔ QɅ┐P

S ↔ (┐PɅQ) V (┐PɅ┐Q) V (PɅQ)    p.d.n.f  PɅQ ↔ QɅP

Here we have used 3 minterms out of 4 to form p.d.n.f

The minterms of P and Q are

P^Q, P^┐Q, ┐P^Q, ┐P^┐Q

Here P^Q, ┐P^Q, ┐P^┐Q are in S.

┐S is nothing but the remaining minterms.

┐S ↔ PɅ┐Q

┐(┐S) ↔ ┐PVQ [Apply duality principle]

i.e.,  S ↔ ┐PVQ [p.c.n.f]

Example 2. Obtain the pdnf of P ↔ Q. Also find pcnf.

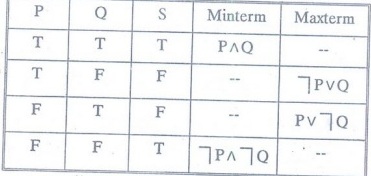
Solution: Let S ↔ P ↔ Q

Method 1.    Truth table

S ↔ (PɅQ) V (┐PɅ┐Q)           pdnf by using minterms

S ↔ (┐P V Q) Ʌ (P V ┐Q)       pcnf by using maxterms.

Method 2:

S ↔ P ↔ Q

↔ (P → Q) Ʌ (Q → P)

 (P ↔ Q) ↔ (P → Q) ^ (Q → P)

↔ (┐PVQ) ^ (┐QVP)

P → Q ↔ ┐PVQ

↔ (┐P^ ┐Q) v (┐P^P) v (Q^┐Q) v (Q^P)    extended distributive lave

↔ (┐P^ ┐Q) v (Q^P)           ┐P^P, Q^┐Q terms droped.

↔ (┐P^ ┐Q) v (P^Q)             P^Q ↔ Q^P

S ↔ (┐P^ ┐Q) v (P^Q)      (pdnf)

┐S ↔ The remaining minterms

↔ (┐P^Q) v (P^┐Q)

Since the minterms of P and Q are

P^Q, P^┐Q, ┐P^Q, ┐P^┐Q

┐(┐S) ↔ Apply duality principle to ┐S

S ↔ (PV┐Q) ^ (┐PVQ)     (pcnf)

Example 3. Obtain PDNF of (PɅQ) V (┐PɅR) V (QɅR) Also find PCNF.  [MCA A/M 2003]

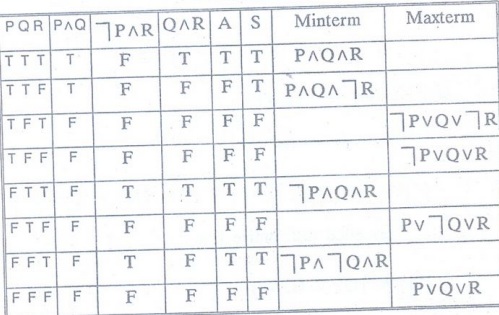
Solution: ↔ Let S (PɅQ) V (┐PɅR) V (QɅR)

Let A = (┐PɅR) V (QɅR)

Truth table

S ⇔ (P^Q^R) V (P^Q^┐R) V (┐P^Q^R) v (┐р^┐Q^R)  (pdnf)

S ⇔ (┐P v Q v ┐R) ^ (┐PVQVR) Ʌ (PV┐QVR) Ʌ (PVQVR)   (pcnf)

Example 4. Without constructing the truth table obtain the product of sums canonical form of the formula.

(┐P → R) Ʌ (Q↔P). Hence find the sum of products canonical form.

[A.U. N/D 2004] [A.U. A/M. 2004]

[A.U. A/M. 2003, A/M 2005, N/D 2005, M/J 2003]

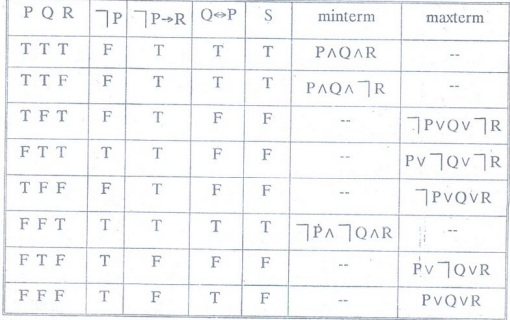
Solution: Let S ↔ (P→R) ^ (Q↔P)

Method 1.  Truth table method

S ⇔ (P^Q^R) V (P^Q^┐R) V (┐р^┐Q^R)  (pdnf)

S ⇔ (┐P v Q v ┐R) Ʌ (PV┐QV┐R) Ʌ (┐PVQVR) Ʌ (PV┐QVR) Ʌ (PVQVR)    (pcnf)

Method 2.

Let S ↔ (P→R) ^ (Q↔P)

 [┐(┐P) VR] ^ [(Q→P) ^ (P→Q)]

P→Q ↔ ┐PVQ, Q↔P ↔ (Q→P) ^ (P→Q)

↔ (PVR) ^ [(┐QVP) ^ (┐PVQ)]

↔ (PVR) ^ (┐QVP) ^ (┐PVQ)

↔ [(PVR) v F] ^ [(┐QVP) v F] ^ [(┐PVQ) VF]    [PVF ↔ P]

↔ [(PVR) v (Q^┐Q) ^ [(┐QVP) V (R Ʌ ┐R)] ^ [(┐PVQ) V (R Ʌ ┐R)]

[QɅ┐Q↔F, RɅ ┐R↔F]    

↔ [(PVRVQ) ^ (PVRV┐Q)] ^ [(┐QVPVR) ^ (┐QVPV┐R) ^ [(┐PVQVR) ^ (┐PVQV┐R)]           by distributive law

↔ [(PVRVQ) ^ (PVRV┐Q) ^ (┐QVPVR) ^ (┐QVPV┐R) ^ (┐PVQVR) ^ (┐PVQV┐R)            PVRV┐Q ↔ ┐QVPVR

S ↔ [(PVQVR) ^ (PV┐QVR) ^ (PV┐QV┐R) ^ (┐PVQVR) ^ (┐PVQV┐R)           pcnf

┐S ↔ The remaining maxterms of P, Q and R

Maxterms of P, Q, R are

(PVQVR), (PvQV┐R), (Pv┐QvR), (┐PVQVR), (Pv┐Qv┐R), (┐PvQv┐R), (┐Pv┐QvR), (┐Pv ┐Qv┐R)

┐S ↔ (PVQV┐R) Ʌ (┐PV┐QVR) Ʌ (┐PV┐QV┐R)

┐ ┐ (S) ↔ Apply duality principle to S

S ↔ (┐PɅ┐Q ɅR) V (PɅQɅ┐R) V (P Ʌ Q Ʌ R) pdnf

Example 5. Obtain the product of sums canonical form for

(PɅQɅR) V (┐PɅQɅR) V (┐PɅ┐QɅ┐R) [A.U. Nov/Dec. 2007]

Solution: Let S ↔ (PɅQɅR) V (┐PɅQɅR) V (┐PɅ┐QɅ┐R pdnf is given.

┐S ↔ The remaining minterms.

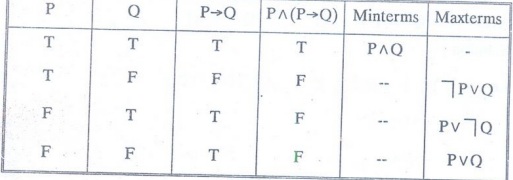
Example 6. Obtain the pcnf and pdnf for PɅ(P→Q)

Solution: Method 1. Truth table

Pdnf = PɅQ by using minterms

Pcnf = (┐PVQ) Ʌ (PV┐Q) Ʌ (PVQ) by using maxterms.

Method 2.

S ↔ P^ (P→Q)

↔ P^ [┐PVQ]

(P→Q) ↔ ┐PVQ

↔ (P^┐P) V (P^Q)   by distributive law

↔ F V (P^Q)

P^┐P ↔ F

↔ P^Q

FVP ↔ P [pdnf]

┐S ↔ The remains minterm

↔ (P^┐Q) V (┐P^Q) V (┐P^┐Q)

┐ (┐S) ↔ Apply duality principle to ┐S

↔ (┐PVQ) Ʌ (PV┐Q) Ʌ (PVQ)

Example 7. Obtain the principal disjunctive and conjuctive normal forms [P→ (QɅR)] ^ [┐P → (┐Q^┐R)]

Solution :

Let S ↔ [P→ (QɅR)] ^ [┐P → (┐Q^┐R)]

A ↔ P→ (QɅR)

B ↔ ┐Q ^ ┐R

C ↔ ┐P → (┐Q^R)]

i.e., ↔ A ^ C

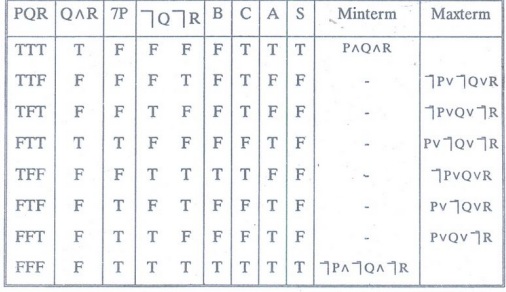
Pdnf = (PɅQɅR) v [┐P ^ ┐Q ^ ┐R)] by using minterms

Pcnf = (┐P v ┐Q v R) ^ (┐P v Q v ┐R) ^ (P v ┐Q v ┐R) ^ (┐P v Q v R) ^ (P v ┐Q v R) ^ (P v Q v ┐R) by using maxterms.

EXERCISE

1. Obtain a d.n.f of the following:

(a) (P ^ ┐(Q ^ R)) v (P→ Q)

(b) (┐P v ┐Q) → (┐P ^ R)

(c) P v (┐Р ^ ┐Q v R)

(d) P→ ((P → Q) ^ ┐(┐Q ^ ┐P)

(e) (Q ^ (P → Q)) → P

(f) (R v ┐P) → ┐(Q → P)

(g) (P → Q) V (P ^ ┐R)

2. Obtain a c.n.f. of the following formulas.

(a) P→ ((P→Q) ^ ┐(┐Q v ┐P))

(b) (P ^ ┐(Q v R) V (((P ^ Q) V┐R) ^ P)

(c) PV (┐P→ (Q v (┐Q → R))

(d) (┐P → R) ^ (Q ↔ P)

(e) Q v (P ^ ┐Q) v (┐P ^ ┐Q)

3. Obtain the p.d.n.f of

(a) P→ ((P → Q) ^ ┐ ( ┐Q v ┐P))

(b) PV (┐P → (Q v (┐Q → R)))

(c) (P^Q) v (┐P^ R) v (Q ^ R)

(d) S↔ (┐PVQVR) Ʌ (P v ┐Q V R) ^ (P V ┐QV ┐R)

(e) P v (┐P V ┐Q V R)

(f) (Q ^ ┐R ^ ┐S) V (R^S)

4. Obtain the p.c.n.f of

(a) (Q → P) ^ ( ┐P ^ Q)

(b) (┐Q ^ R) v (┐Q ^ ┐R ^ P)

(c) (┐P → R) ^ (P ↔ Q)

(d) (┐Р → R) ^ (Q ↔ P)

S: P v (┐P → (Q v (┐Q → R)))

5. Obtain the PCNF and PDNF of

(a) (P→ (Q^R)) ^ (┐р→ (┐Q Ʌ ┐R)

(b) (P Ʌ Q) V (┐P Ʌ Q) V (Q Ʌ R)

(c) (P V Q) Ʌ (┐P v Q V R)

Normal Forms: Order, Uniqueness

Normal forms: PCNF, PDNF are unique except for the rearrangements of the factors in the disjunctions / conjunctions as well as in each of the minterms / maxterms.

Now, we can get a unique normal form by imposing a certain order in which the variables appear in the minterms (maxterms) as well as definite order in which minterm (maxterms) appear in the disjunction (conjuction)

 (1) Let us assume that n variables are given and are arranged in a particular order. The 2ⁿ minterms corresponding to the n variables can be designated m₀, m₁, … m(2ⁿ) - 1.

Thus each of m₀, m₁, ..., m(2ⁿ)-1 corresponds to a unique minterm, which can be determined from the binary representation of its subscript (the number of digit in the subscript is exactly n). We can obtain minterm is the following ma^er :

If 1 appears in the i^th location from the left, then the i^th variable appears in the conjunction.

If 0 appears in the i^th location from the left, then the negation of the i^th variable appears in the conjunction forming the minterm.

Conversely, given any minterm, one can find which of m₀, m₁, ..., m(2ⁿ)-1 designates it.

Example 1. Let P, Q and R be three Variables arranged in that order. The corresponding minterms are denoted by m₀, m₁, …. m₇(2³-1=7)

Consider m₅, the subscript 5 in binary as 101 and the minterm m₅ is PɅ┐QɅR. Similarly m₀ corresponds to ┐P Ʌ ┐Q Ʌ ┐R. To obtain the minterm m₃, we write the subscript 3 in binary as 11 and append a zero on the left to get 011 and m₃ is ┐PɅQɅR.

With the above notation for the representation of the minterms we designate the disjunction (Sum) of minterms by the compact notation Σ.

Using such a notation, the sum-of-products canonical form representing the disjunction of m_i, m_j and m_k can be written down as Σ i,j,k.

Example 2. The p.d.n.f of (P^Q)v(┐P^R)v(QVR) is (┐P^┐Q^R) v (┐P^Q^R) V(P^QɅ┐R)V(P^Q^R), From the previous notation: we denote the p.d.n.f as Σ 1, 3, 6, 7.

II. The 2ⁿ maxterms corresponding to the n statement Variables can be designated by M₀, M₁,… M(2ⁿ)-1. Here also the maxterms corresponding to M_j is obtained by writing j in binary and appending the required number of zeros to the left in order to get n digits.

If 0 appears in the i^th location from the left of this binary number, then the i^th variable appears in the disjunction. If 1 appears in the i^th location, then the negation of the i^th variable appears.

Thus the binary representation of the subscript uniquely determines the maxterm. Conversely every binary representation of numbers between 0 and 2ⁿ-1 determines a maxterm.

Note that the convention regarding 1 and 0 here is the opposite of what was used for minterms.

Example 3. The maxterms M₀, M₁, ..., M₇ corresponding to three variables P, Q and R are

PVQVR   PVQV┐R   PV┐QVR    PV┐QV┐R

┐PVQVR    ┐PVQV┐R    ┐PV┐QVR    ┐PV┐QV┐R

with the above notation for the representation of the maxterms we designate the conjunction (product) of maxterms by the compact notation ∏.

Thus ∏ i,j,k represents the conjuction of maxterms M_i, M_j, M_k.

Example 4. The PCNF of (P^Q)v(┐P^R): (┐PɅQVR) Ʌ (┐PVQV┐R) ^ (PVQVR)^(PV┐QVR) it can be represented as ∏ 0, 2, 4, 5.