NOR-NOR Implementation

NOR-NOR Implementation    AU: May-11

• The NOR function is a dual of the NAND function. For this reason, the implementation procedures and rules for NOR-NOR logic are the duals of the corresponding procedures and rules developed for NAND-NAND logic.

• The implementation of a Boolean function with NOR-NOR logic requires that the function be simplified in the product of the sum form.

• In product of sum form, we implement all sum terms using Or gates.This constitutes the first level.

• In the second level all sum terms are logically ANDed using AND gate. The relationship between OR-AND logic and NOR-NOR is explained using following example.

• Consider the Boolean function : Y =(A + B + C) (D + E) F

• This Boolean function can be implemented using OR-AND logic, as shown in the Fig. 1.9.1 (a).

• Fig. 1.9.1 (b) shows the OR gates are replaced by NOR gates and the AND gate is replaced by a bubbled AND gate. The implementation shown in Fig. 2.16.1 (b) is equivalent to implementation shown in Fig. 2.16.1 (a), because two bubbled on the same line represent double inversion (complementation) which is equivalent to having no bubble on the line.

• In case of single variable, F, the complemented variable again complemented by bubble to produce the normal value of F.

• In Fig. 1.9.1 (c), the output NOR gate is redrawn with the conventional symbol. The NOR gate with same inputs gives complemented result, therefore, is replaced by NOR gate with F input to its both inputs. Thus all the three implementations of Boolean function are equivalent.

Rules for obtaining the NOR-NOR logic diagram

1. Simplify the given Boolean function and express it in product of sum form (POS form).

2. Draw a NOR gate for each sum term of the function that has two or more literals. The inputs to each NOR gate are the literals of the term. This constitute a group of first level gates.

3. If Boolean function includes any single literal or literals, draw NOR gate for each single literal and connect corresponding literal as an input to the NOR gate.

4. Draw a single NOR gate in the second level, with inputs coming from outputs of first level gates.

Illustrative Examples

Example 1.9.1 Implement the following Boolean function with NOR-NOR logic

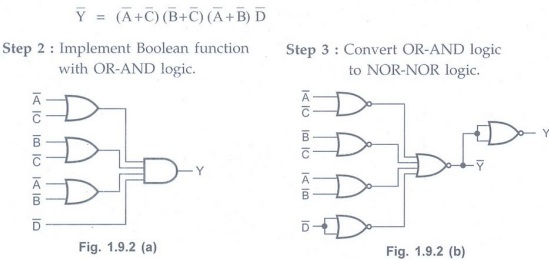
Y=AC+BC+ A B+ D.

Solution: Step 1: Express Boolean function in POS form.

Using duality theorem we get,

Example 1.9.2 Implement the following Boolean function with NOR-NOR logic. F = (A, B, C) = II M (0, 2, 4, 5, 6)

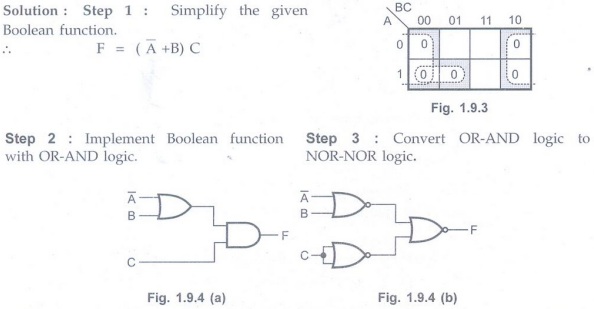
Note It is possible to directly go to step 3 skipping step 2. Here, step 2 is included for clear understanding.

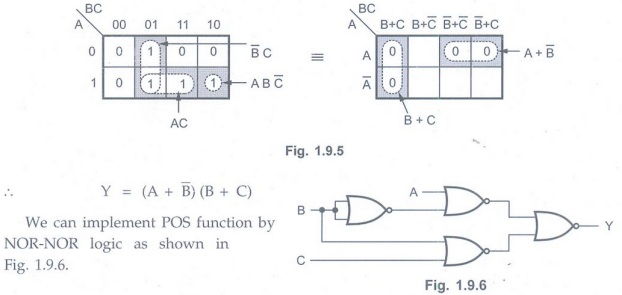
Example 1.9.3 Design a combinational circuit that comprises only of NOR gates for the following expression giving the input output relation.

Y = ABC' + AC + B'C.      AU May-11, Marks 10

Solution :