Theory of Computation: Unit I: Automata and Regular Expressions
Non-deterministic Finite Automata (NFA)
Automata and Regular Expressions - Theory of Computation
The concept of Non-deterministic Finite Automata is exactly reverse of Deterministic Finite Automata. The Finite Automata is called NFA when there exists many paths for a specific input from current state to next state.
Non-deterministic
Finite Automata (NFA)
AU: May-09,12, Marks 8
•
The concept of Non-deterministic Finite Automata is exactly reverse of Deterministic
Finite Automata. The Finite Automata is called NFA when there exists many paths
for a specific input from current state to next state. The NFA can be shown as
in Fig. 1.7.1
•
Note that the NFA shows from q0 for input a there are two next
states q1 and q2. Similarly, from q0 for input
b the next states are q0 and q1.
•
Thus it is not fixed or determined that Fig. 1.7.1 Non-deterministic finite automata
with a particular input where to go next. Hence this FA is called
non-deterministic finite automata.

•
Consider the input string bba. This
string can be derived as
Input
b
b a
Path
q0 q0 q1
Input
b
b a
Path q0 q0 q2
Input
b
b a
Path q0 q1 q1
Thus
you cannot take the decision of which path has to be followed for deriving the
given string.
Definition of NFA
The
NFA can be formally defined as a collection of 5-tuples.
1)
Q is a finite set of states.
2)
Σ is a finite set of inputs.
3)
δ is called next state or transition function.
4)
q0 is initial state.
5)
F is a final state where F![]() Q.
Q.
There
can be multiple final states. Thus the next question might be what is the use
of NFA. The NFA is basically used in theory of computations because they are
more flexible and easier to use than the DFAs.
Difference between NFA and DFA

Example 1.7.1
Construct a NFA for a language L which
accepts all the strings in which the third symbol from right end is always a.
Over Σ= {a, b}.
Solution:
•
Logic: The strings in such a
language are of the form

Thus
we get third symbol from right end as 'a' always. The NFA then can be
• Design:
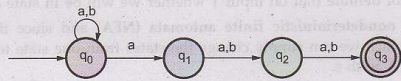
The
above figure is a NFA because in state q0 with input 'a' we can go
to either state q0 or state q1.
Example 1.7.2
Draw state transition diagram for FA over
{a, b} containing substring aabb.
AU: May-09, Marks 4
Solution:
The FA can be

Example 1.7.3
Construct NFA accepting binary strings
with two consecutive 0's. AU:
May-12, Marks 8
Solution:
For constructing this NFA the input set Σ ={0,1}. The NFA will be -
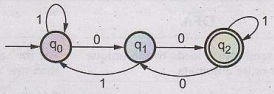
Theory of Computation: Unit I: Automata and Regular Expressions : Tag: : Automata and Regular Expressions - Theory of Computation - Non-deterministic Finite Automata (NFA)
Related Topics
Related Subjects
Theory of Computation
CS3452 4th Semester CSE Dept | 2021 Regulation | 4th Semester CSE Dept 2021 Regulation
