Minimization of DFA

Minimization of DFA

AU Dec.-18, May-13, 14, 16, Marks 10

The minimization of FSM means reducing the number of states from given FA. Thus we get the FSM with redundant states after minimizing the FSM.

While minimizing FSM we first find out which two states are equivalent we can represent those two states by one representative state.

The two states q₁ and q₂ are equivalent if both δ (q₁, x) and δ (q₂, x) are final states or both of them are non final states for all x ϵ Σ* (Σ* indicate any string of any length) we can minimize the given FSM by finding equivalent states.

Example 1.12.1 Minimize the DFA as given below. AU May-16, Marks 8

Solution :

We will build the transition table for given DFA, as follows:

Step 1: We will build a table in following format for finding equivalent states and mark final and non-final states with x

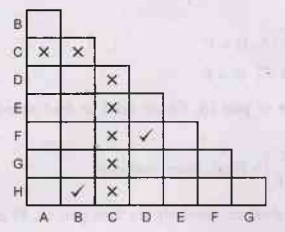
Step 2: The states that need to be marked are (A, B), (A, D), (A, E), (A, F), (A, G), (A, H), (B, D), (B, E), (B, F), (B, G), (B, H), (D, E), (D, F), (D, G), (D, H), (E, F), (E, G), (E, H), (F, G), (F, H), (G, H).

If we observe transition table then

δ (B, 0) = G

δ (B, 1) = C

δ (H, 0) = G

δ (H, 1) = C

Similarly

δ (D, 0) = C

δ (D, 1) = G

δ (F, 0) = C

δ (F, 1) = G

Thus pairs (B, H) and (D, F) are equivalent

Step 3:

Step 4:

Now, consider pair (A, E)

Pair (A, E) is equivalent

Step 5: i) Pair (A, B)

δ (A, 0) = B    δ (A, 1) = F → Final, Non Final states

δ (B, 0) = G    δ (B, 1) = C → Final, Non Final states

Pair (A, B) is not equivalent

ii) Pair (A, D)

Pair (A, F) is not equivalent.

iv) Pair (A, G)

δ (A, 0) = B     δ (A, 1) = F

δ (G, 0) = G     δ (G, 1) = E

To decide equivalence of pair (A, G) we need to find equivalence of pair (B, G) and (E, F)

δ (B, 0) = G     δ (B, 1) = C → Final, Non-Final pair

δ (G, 0) = G     δ (G, 1) = E → Final, Non Final pair

Pair (B, G) is not equivalent. Similarly we find pair (E, F) and ultimately pair (A, G) are not equivalent.

v) Pair (A, H)   

δ (A, 0) = B     δ (A, 1) = F → Final, Non-Final pair

δ (H, 0) = G     δ (H, 1) = C → Final, Non-Final pair

Pair (A, H) is not equivalent

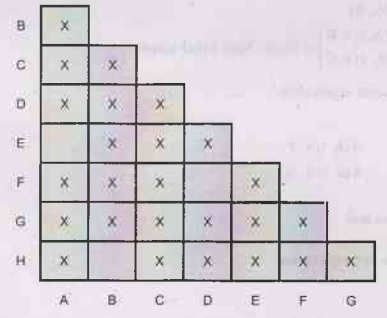
Step 6: In this way, we find pairs (A, E), (B, H) and (D, E) are only equivalent pairs and all other remaining pairs are not equivalent.

Thus we get equivalent pairs as (A, E), (B, H), (D, F). Hence the minimized DFA will be,

Example 1.12.2 Minimize the

AU Dec.-18, Marks 7

Solution: We will construct table as follows

We will mark final and non-final state by x

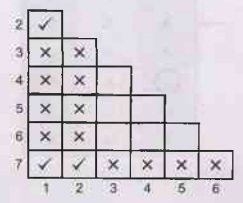
Now we will find the equivalence of the pairs (3, 4), (3, 5), (3, 6), (4, 5), (4, 6),(5, 6),

Pair (3, 4)

δ (3, a) = 6      δ (3, b) = 7    → Final, Non Final Pair

δ (4, a) = 5      δ (4, b) = 4    → Final, Non Final Pair

Hence put x in (3, 4)

Pair (3, 5)

δ (3, a) = 6     δ (3, b) = 7 → Final, Non Final Pair

δ (5, a) = 7     δ (5, b) = 5 → Final, Non Final Pair

Hence put x in (3, 5)

Pair (3, 6)

δ (3, a) = 6    δ (6, a) = 2 → Final, Non Final Pair

δ (3, b) = 7    δ (6, b) = 7

Hence put x in (3, 6)

Pair (4, 5)

δ (4, a) = 5    δ (5, a) = 7  → Final, non final pair

δ (4, b) = 4   δ (5, b) = 5

Hence put x in (4, 5)

Pair (4, 6)

Pair (5, 6)

δ (5, a) = 7     δ (5, b) = 5 → Final, Non Final Pair

δ (6, a) = 2     δ (6, b) = 7 → Final, Non Final Pair

Hence put x in (5, 6)

Thus we do not get any of the mentioned pairs as equivalent pair.

The only equivalent pairs are (1, 2), (1, 7), (2, 7)

We assume state 1 = 2 = 7. We eliminate state 2 and 7 by replacing them by 1.

The minimized DFA can be given by following transition table.

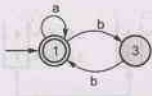
But, since state 4 and 5 are not reachable from start state 1, we eliminate them. Also, state 6 is a dead state. Hence, minimizes DFA is

Example 1.12.3 Define distinguishable and indistinguishable states. Using table filling method, minimize the following DFA. Draw the transition diagram of resulting DFA.

Solution: Distinguishable and indistinguishable states: If for some input string w, δ (p w) gives an accepting state and δ (q, w) gives a non-accepting state or vice versa then states p and q are called distinguishable states or non-equivalent states.

If for some input string w, δ (p, w) and δ (q, w) both produces either accepting states or non-accepting states, then states p and q are called indistinguishable or equivalent states.

We will apply a table filling method for minimizing the given DFA.

We will mark X in a final and non-final pairs. Now we will consider each pair and check for its equivalence consider pair G, H.

δ (G, 0) = H and δ (G, 1) = B

δ (H, 0) = I and δ (H, 1) = C

Since pairs (H, I) and (B, C) are already marked X, pair (G, H) is not equivalent so we will mark X in pair (G, H).

Now, consider pair (E, H),

 δ (E, 0) = F and δ (E, 1) = I

δ (H, 0) = I and δ (H, 1) = C

As (F, I) and (I, C) both are final states, hence pair (E, H) is said to be equivalent and we won't put X in the pair (E, H).

Now, consider pair (E, G),

δ (E, 0) = F and δ (E, 1) = I

δ (G, 0) = H and δ (G, 1) = B

As pairs (F, H) and (I, B) have X, we put X in (E, G).

Consider pair (E, F),

δ (E, 0) = F and δ (E, 1) = I

δ (F, 0) = G and δ (F, 1) = B

Put X in pair (E, F). Hence table will be

Consider pairs (D, H), (D, G), (D, F), (D, E) out of which

δ (D, 0) = E and δ (D, 1) = H

δ (H, 0) = I and δ (H, 1) = C

Hence put X in (D, H),

δ (D, 0) = E    δ (D, 1) = H

δ (G, 0) = H   δ (G, 1) = B

Pair (E, H) is equivalent. For pair (H, B) we will find their input transitions. Both state H and state B yield final states we say pair (D, G) is equivalent at the same time we find pair (H, B) as equivalent.

δ (D, 0) = E and δ (D, 1) = H

δ (F, 0) = G and δ (F, 1) = B

As pair (E, G) is having X we will put X in (D, F).

Consider pair (D, E),

δ (D, 0) = E   δ (D, 1) = H

δ (E, 0) = F    δ (E, 1) = I

Pair (D, E) is not matching, put X in (D, E).

Consider pair (B, G),

δ (B, 0) = C    δ (B, 1) = F

δ (G, 0) = H    δ (G, 1) = B

As pair (C, H) is not equivalent put X in (B, G).

Consider pair (B, F),

δ (B, 0) = C    δ (B, 1) = F

δ (F, 0) = G    δ (F, 1) = B

As pair (C, G) is having X, we put X in (B, F).

Consider pair (B, E),

δ (B, 0) = C    δ (B, 1) = F

δ (E, 0) = F     δ (E, 1) = I

As (C, F) and (F, I) are both final states we say pair (B, E) is equivalent.

Consider pair (D, B),

δ (B, 0) = C    δ (B, 1) = F

δ (D, 0) = E    δ (D, 1) = H

As pair (E, C) have X, we put X in pair (D, B).

Consider pair (A, H),

δ (A, 0) = B    δ (A, 1) = E

δ (H, 0) = I     δ (H, 1) = C

As X is in pair (B, I) we put X in (A, H).

Consider pair (A, G),

δ (A, 0) = B    δ (A, 1) = E

δ (G, 0) = H    δ (G, 1) = B

As pairs (B, H) and (B, E) are equivalent.

We can say pair (A, G) is equivalent.

Consider pair (A, E),

δ (A, 0) = B     δ (A, 1) = E

δ (E, 0) = F      δ (E, 1) = I

As (B, F) have X we will put X in (A, E) pair (A, D) is already equivalent.

Consider pair (A, B),

δ (A, 0) = B    δ (A, 1) = E

δ (B, 0) = C    δ (B, 1) = F

As pair (B, C) have X, we will put X in (A, B).

Hence finally table will be,

The blank entries represent equivalent states

State A = G = D

State B = H = E

State C = I = F

Hence reduced DFA will be,

Example 1.12.4 Minimize the Finite automaton Fig. 1.12.2 below and show both the given and the reduced one are equivalent.

AU May-14, Marks 10

Solution: We will first construct the transition table for given DFA -

Now we will partition the states Q in Q₁⁰ and Q₂⁰. The state q₄ is a final state. Hence

Q₁⁰= F = {q₄}

Q₂⁰ = Q – Q₁⁰ = {q₀, q₁, q₂, q₃)

П₀ = {{q₄}, {q₀, q₁, q₂, q₃}}

Now we will compare q₀ with q₁. We find that under 0 column we get q₁ and q₂. And q₁ and q₂ lie in the same set i.e. Q₂. But under 1-column of q₀ and q₁ we get q₃, q₄ respectively. But q₃ ϵ Q₂⁰ and q₄ ϵ Q₁⁰. Hence they are not 1- equivalent.

Similarly compare q₀ and q₂. We will find that under 0 column of q₀ and q₂ we get q₁ only. But under 1-column of q₀ and q₂ we get q₃ and q₄. The q₃ ϵ Q₂ and q₄ ϵ Q₁.

Hence q₀ and q₂ are not 1 - equivalent. Similarly q₀ is not 1 - equivalent to q₃ because of 1 column entries.

Q'₁ = {q₄}

Q'₂ = {q₀}

Q'₃ = {q₁, q₂, q₃}

Hence, II₁ = {{q₄}, {q₀}, {q₁, q₂, q₃}}

Now in set (q₁, q₂, q₃) we compare q₁ with q₂ under 0-column we get q₂ and q₁ which are in the same set, and under 1 - column we get q₄. And for state q₁ and q₃ we get same entries under 0 column and under 1 - column. Hence we can group them {q₂, q₃}.

The equivalence class becomes,

П₂ = {{q₄}, {q₀}, {q₁}, {q₂, q₃}}

Now further we cannot partition any of the set. We get

П₃ = {{q₀}, {q₂}, {q₄}, {q₁, q₃}}

Review Question

1. Discuss on the relation between DFA and minimal DFA. AU: May-13, Marks 6