Min-Max Algorithm

Mini-Max Algorithm

AU: Dec.-03, 04, May-09, 10, 17, 19

The minimax algorithm computes the minimax decision from the current state. It is used as a searching technique in game problems. The minimax algorithm performs a complete depth-first exploration of the game-tree.

Concept of Mini-Max Algorithm

1. The start node is MAX (player 1) node with current board configuration.

2. Expand nodes down (play) to some depth of look-ahead in the game.

3. Apply evaluation function at each of the leaf nodes.

4. "Back up" values for each non-leaf nodes until computed for the root node.

5. At MIN (player 2) nodes, the backed up value is the minimum of the values associated with its children.

6. At MAX nodes, the backed up value is the maximum of the values associated with its children.

Note The process of "backing up" values gives the optimal strategy, that is, both players assume that your opponent is using the same static evaluation function as you are.

Properties of Mini-Max

1. Minimax provides a complete solution for finite tree.

2. Minimax provides optimal strategy against an optimal opponent.

3. The time complexity is O(b^m).

4. The space complexity is O(b^m) for depth-first exploration where algorithm generates all successor at once, or O(m) for an algorithm that generate successors one at a time.

Problem Associated with Mini-Max

This algorithm explores whole search space. If we have a game with huge search spaces it will take long time.

In such cases then exact solution is completely infeasible.

Game Playing with Mini-Max-Tic-Tac-Toe [Noughts and crosses] Example

1. Assume that two players named MIN and MAX who are playing the game.

2. MAX is playing first.

3. As you can see initially MAX has nine possbile moves.

4. Play alternates between MAX and MIN until we reach leaf nodes corresponding to terminal states such that one player has 3 in a row or all the squares are filled.

5. The number on each leaf node indicates the utility value of the terminal state from the point of view of MAX.

6. High values are assumed to be good for MAX and bad for MIN.

7. It is MAX's job to make use of search tree to determine best move.

8. Static evaluation. Criteria + 1' for a win, '0' for draw.

Example to show how Mini-Max Algorithm Works

Consider game of tic-tac-toe with the initial state -

Step 1:

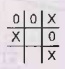
Start: MAX (player 1) moves (MAX is making X)

Step 2: Next: MIN (player 2) moves.

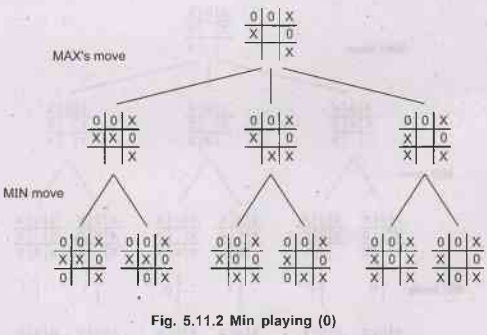
Step 3: Again: MAX's moves

Step 4: +1' for a win, '0' for a draw. Criteria '+ 1' for a win, '0' for a draw.

Step 5: Level by level, on the basis of opponents turn UP: One level

Step 6: UP: Two levels

Step 7: Choose best move which is maximum

The 'made-up' Games and Concept of 'ply'

For study purpose we can form a game a tree which is constructed up to certain level (i.e. upto certain depth). This is called as a made-up game. The term ply refers to depth of the tree.

For example - ply 4 is level at depth 4 below the root node.

Example

A two ply game tree, for game of tic-tac-toe.

1. Assume that two players named MIN and MAX who are playing the game.

2. MAX is playing first.

3. The possible moves for MAX at the root node are labeled a1, a2 and a3.

4. The possible replies to a 1 for MIN are b1, b2, b3 and so on.

5. This particular game ends after one move each by MAX and MIN.

6. In game parlance, we say that this tree is one which, moves deep consisting of two-half-moves, each of which is called a ply.

Example

A three-ply game tree, for game of tic-tac-toe

Mini-Max Algorithm for Playing Multiplayer Games

1. There are many multiplayer games like cricket, football, etc.

2. The multiplayer game can be played with minimax concept.

3. Here the single value for each node is replaced with a vector of values. For example, in a three-player game with players A, B, and C a vector (V_A , V_B , V_C) is associated with each node.

4. For terminal states, this vector gives the utility of the state from each player's viewpoint. (In two player, zero-sum games, the two-element vector can be reduced to a single value because the values are always opposite.

5. In this implementation UTILITY function return a vector of utilities.

6. For non-terminal states we can calculate utility function value as explain below - Consider following diagram,

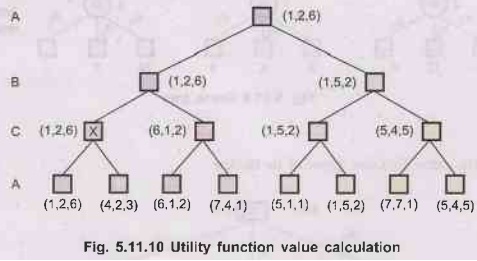
7. For non-terminal states vector values should be calculated as explained. Consider the node marked X in the game tree shown in above diagram. In this state, player C choose what to do. The two choices lead to terminal states with utility vector (V_A = 1, V_B = 2, V_C  = 6) and  (V_A = 4, V_B = 2, V_C  = 3). Since 6 is bigger than 3, C should choose the first move. This means that if state X is reached subsequent play will lead to a terminal state with utilities  (V_A = 1, V_B = 2, V_C  = 6).  Hence the backed-up value of X is this vector.

8. In general, the backed-up value of a node 'n' is the utility vector of whichever successor has the highest value for the player choosing at 'n'.