Merge Sort

Merge Sort

AU Dec.-15, 18, May-19, Marks 13

Merge sort is a sorting algorithm in which array is divided repeatedly. The sub arrays are sorted independently and then these subarrays are combined together to form a final sorted list.

Merge sort on an input array with n elements consists of three steps:

Divide: partition array into two sub lists s1 and s2 with n/2 elements each.

Conquer: Then sort sub list s1 and sub list s2.

Combine merge s1 and s2 into a unique sorted group.

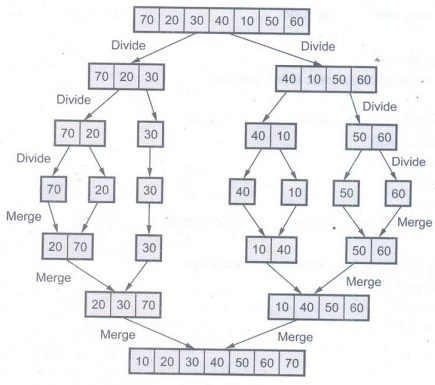
Ex. 6.8.1: Consider the following elements for sorting using merge sort

70, 20, 30, 40, 10, 50, 60

Sol. Now we will split this list into two sublists.

Algorithm

Algorithm MergeSort(int A[0...n-1],low,high)

 //Problem Description: This algorithm is for

//sorting the elements using merge sort

//Input: Array A of unsorted elements, low as //beginning

 //pointer of array A and high as end pointer of array A

//Output: Sorted array A[0...n-1]

if(low < high)then

{

mid←(low+high)/2  //split the list at mid

MergeSort(A,low,mid) //first sublist

MergeSort(A,mid+1,high) //second sublist

Combine(A,low,mid,high) //merging of two sublists

}

Algorithm Combine(A[0...n-1],low, mid, high)

{

K←low; //k as index for array temp

i← low;//i as index for left sublist of array A

j← mid+1 //j as index for right sublist of array A

 while(i <= mid and j <= high)do

{

if(A[i]<=A[j])then

//if smaller element is present in left sublist

{

//copy that smaller element to temp array

temp[k] ← Ali]

i←i+1

k←k+1

}

else //smaller element is present in right sublist

{

//copy that smaller element to temp array

temp[k] ← Alj]

j←j+1

k←k+1

}

}

//copy remaining elements of left sublist to temp

 while(i<=mid)do

{

temp[k] ←A[i]

i←i+1

k←k+1

}

//copy remaining elements of right sublist to temp

while(j<=high)do

{

temp[k] ←A[j]

j←j+1

k←k+1

}

Logic Explanation

To understand above algorithm consider a list of elements as

Consider that at some instance we have got two sublits 20, 30, 40, 70 and 10, 50, 60, then

Finally we will copy all the elements of array temp to array A. Thus array A contains sorted list.

C Function

void MergeSort(int A[10], int low, int high)

{

int mid;

void Combine(int A[10]; int low, int mid, int high);

if(low high)

{

mid = (low+high)/2; //split the list at mid

MergeSort (A,low,mid); //first sublist

MergeSort(a,mid+1,high); //second sublist

 Combine(A,low,mid, high); //merging of two

sublists

}

}

void Combine(int A[10], int low, int mid, int high)

{

int i,j,k;

int temp[10];

k=low;

i=low;

j=mid+1;

while(i <= mid && j <= high)

{

if(A[i]<=A[j])

{

temp[k] =A[i];

i++;

k++;

}

else

{

temp[k]=A[j];

j++;

k++;

}

}

while(i<=mid)

{

temp[k] =A[i];

i++;

k++;

}

while (j<=high)

{

temp[k]=A[j];

j++;

k++;

}

//copy the elements from temp array to A

for(k=low;k<=high;k++)

A[k]=temp[k];

}

C Program

/***************************************************************

This program is for performing Merge Sort.

***************************************************************/

#include <conio.h>

#include<stdio.h>

#include<stdlib.h>

int n;

void main()

{

int i,low,high;

int A[10];

void MergeSort(int A[10], int low,int high);

void Display(int A[10]);

clrscr();

printf("\n\t\t Merge Sort \n");

printf("\n Enter the length of list :");

scanf("%d",&n);

printf("\n Enter the list elements:");

for(i=0;i<n;i++)

scanf("%d", &A[i]);

low=0;

high=n-1;

MergeSort(A,low,high);

Display(A);

getch();

}

/*

This function is to split the list into sublists

*/

void MergeSort(int A[10], int low,int high)

{

int mid;

void Combine(int A[10], int low, int mid,int high);

if(low < high)

{

Mid=(low+high)/2;//split the list at mid

MergeSort(A,low,mid);//first sublist

MergeSort(A,mid+1,high);//second sublist

Combine(A,low,mid,high);//merging of two sublists

}

}

/* This function is for merging the two sublists

*/

void Combine(int A[10], int low,int mid,int high)

{

int i,j,k;

int temp[10];

k=low;

i=low;

j=mid+1;

while(i<= mid && j <= = high)

{

if(A[i]<=A[j])

{

temp[k]=A[i];

i++;

k++;

}

else

{

temp[k]=A[j];

j++;

k++;

}

}

while(i<=mid)

{

temp[k]=A[i];

i++;

k++;

}

while(j<=high)

{

temp[k] =A[j];

j++;

k++;

}

//copy the elements from temp array to A

for(k=low;k<=high;k++)

A[k]=temp[k];

}

/* function to display sorted array */

void Display(int A[10])

{

int i;

printf("\n\n The Sorted Array Is ...\n");

for(i=0;i<n;i++)

printf("%d\t",A[i]);

}

Output

 Merge Sort

Enter the length of list :7

Enter list elements

70

20

30

40

10

50

60

The Sorted Array Is

10 20 30 40 50 60 70

Ex. 6.8.2 Sort the following numbers using merge sort algorithm 11, 8, 55, 22, 33, 27, 62, 35, 71. Obtain the worst case and average case time complexity

Sol. :

Time Complexity

The recurrence relation for merge sort is as given below -

T (n)  =  T (n/2)                +  T(n/2)                 +         cn

        Time taken by           Time taken by     Time taken for         

         Left sublist to             right sublist to   combining two

         Get sorted                   get sorted              sublists

where n > 1, T (1) = 0

Let, the recurrence relation for Merge Sort be,

T(n)=T(n/2) + T(n/2) + cn    for n > 1

i.e.  T(n)= 2T(n/2) + cn        for n > 1   …..(1)

T(1)= 0  …..(2)

Let us apply substitution on equation (1). Assume n = 2^k.

T(n)=2T(n/2) + cn

T(n)=2T(2^k/2) + c2^k

It we put k = k - 1 then,

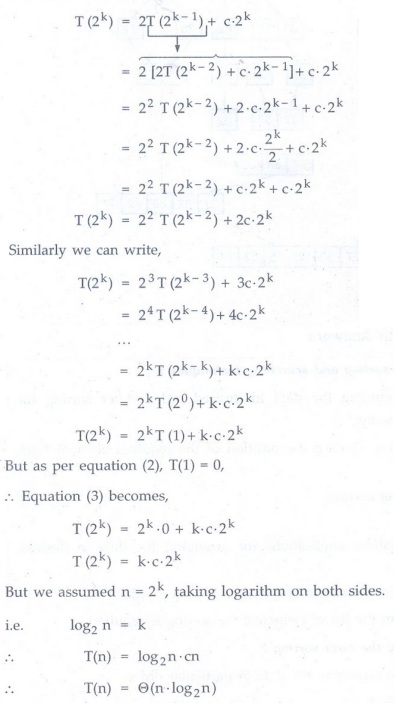
Hence the average and worst case time complexity of merge sort is Ɵ(n log₂n)

Review Question

1. Write a function to perform merge sort. Give example.

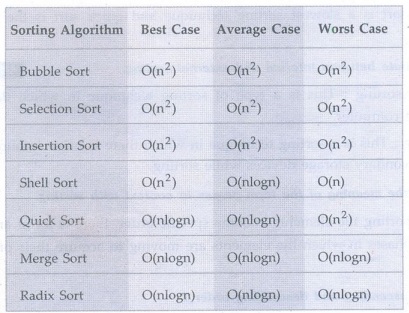
Time Complexity Analysis