Maximum Margin Classifier: Support Vector Machine

Maximum Margin Classifier: Support Vector Machine

Support Vector Machines (SVMs)are a set of supervised learning methods which learn from the and used for dataset classification. SVM is a classifier derived from statistical learning theory by Chervonenkis.

• An SVM is a kind of large-margin classifier: It is a vector space based machine learning method where the goal is to find a decision boundary between two classes that is maximally far from any point in the training data

• Given a set of training examples, each marked as belonging to one of two classes, an SVM algorithm builds a model that predicts whether a new example falls into one class or the other. Simply speaking, we can think of an SVM model as representing the examples as points in space, mapped so that each of the examples of the separate classes are divided by a gap that is as wide as possible.

• New examples are then mapped into the same space and classified to belong to the class based on which side of the gap they fall on.

Two Class Problems

• Many decision boundaries can separate these two classes. Which one should we choose?

• Perceptron learning rule can be used to find any decision boundary between class 1 and class 2.

• The line that maximizes the minimum margin is a good bet. The model class of "hyper-planes with a margin of m" has a low VC dimension if m is big.

• This maximum-margin separator is determined by a subset of the data points. Data points in this subset are called "support vectors". It will be useful computationally if only a small fraction of the data points are support vectors, because we use the support vectors to decide which side of the separator a test case is on.

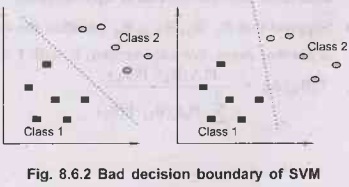
Example of Bad Decision Boundaries

• SVM are primarily two-class classifiers with the distinct characteristic that they aim to find the optimal hyperplane such that the expected generalization error is minimized. Instead of directly minimizing the empirical risk calculated from the training data, SVMs perform structural risk minimization to achieve good generalization.

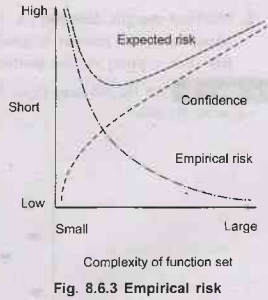
• The empirical risk is the average loss of an estimator for a finite set of data drawn from P. The idea of risk minimization is not only measure the performance of an estimator by its risk, but to actually search for the estimator that minimizes risk over distribution P. Because we don't know distribution P we instead minimize empirical risk over a training dataset drawn from P. This general learning technique is called empirical risk minimization.

• Fig. 8.6.3 shows empirical risk.

Good Decision Boundary: Margin Should Be Large

• The decision boundary should be as far away from the data of both classes as possible. If data points lie very close to the boundary, the classifier may be consistent but is more "likely" to make errors on new instances from the distribution. Hence, we prefer classifiers that maximize the minimal distance of data points to the separator.

1. Margin (m): the gap between data points & the classifier boundary. The Margin is the minimum distance of any sample to the decision boundary. If this hyperplane is in the canonical form, the margin can be measured by the length of the weight vector.The margin is given by the projection of the distance between these two points on the direction perpendicular to the hyperplane.

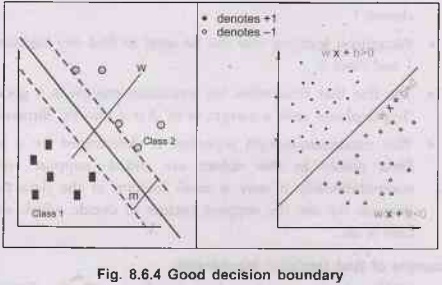
Margin of the separator is the distance between support vectors.

Margin (m)= 2/|w|||

2. Maximal margin classifier: a classifier in the family F that maximizes the margin. Maximizing the margin is good according to intuition and PAC theory. Implies that only support vectors matter; other training examples are ignorable.

Example 8.6.1 For the following figure find a linear hyperplane (decision boundary) that will separate the data.

Solution:

1. Define what an optimal hyperplane is : maximize margin

2. Extend the above definition for non-linearly separable problems have a penalty term for misclassifications

3. Map data to high dimensional space where it is easier to classify with linear of by decision surfaces: reformulate problem so that data is mapped implicitly to this space

Key Properties of Support Vector Machines

1. Use a single hyperplane which subdivides the space into two half-spaces, one which is occupied by Class 1 and the other by Class 2

2. They maximize the margin of the decision boundary using quadratic optimization techniques which find the optimal hyperplane.

3. Ability to handle large feature spaces.

4. Overfitting can be controlled by soft margin approach

5. When used in practice, SVM approaches frequently map the examples to a higher dimensional space and find margin maximal hyperplanes in the mapped space, obtaining decision boundaries which are not hyperplanes in the original space.

6. The most popular versions of SVMs use non-linear kernel functions and map the attribute space into a higher dimensional space to facilitate finding "good" linear decision boundaries in the modified space.

SVM Applications

• SVM has been used successfully in many real-world problems,

1. Text (and hypertext) categorization

2. Image classification

3. Bioinformatics (Protein classification, Cancer classification)

4.Hand-written character recognition

5. Determination of SPAM email.

Limitations of SVM

1. It is sensitive to noise.

2. The biggest limitation of SVM lies in the choice of the kernel.

3. Another limitation is speed and size.

4. The optimal design for multiclass SVM classifiers is also a research area.

Soft Margin SVM

• For the very high dimensional problems common in text classification, sometimes the data are linearly separable. But in the general case they are not, and even if they are, we might prefer a solution that better separates the bulk of the data 1st while ignoring a few weird noise documents.

• What if the training set is not linearly separable? Slack variables can be added to allow misclassification of difficult or noisy examples, resulting margin called soft.

• A soft-margin allows a few variables to cross into the margin or over the hyperplane, allowing misclassification.

• We penalize the crossover by looking at the number and distance of the misclassifications. This is a trade off between the hyperplane violations and the margin size. The slack variables are bounded by some set cost. The farther they are from the soft margin, the less influence they have on the prediction.

• All observations have an associated slack variable,

1. Slack variable = 0 then all points on the margin.

2.Slack variable > 0 then a point in the margin or on the wrong side of the hyperplane

3. C is the trade off between the slack variable penalty and the margin.

Comparison of SVM and Neural Networks

Example 8.6.2 From the following diagram, identify which data points (1, 2, 3, 4, 5) are support vectors (if any), slack variables on correct side of classifier (if any) and slack variables on wrong side of classifier (if any). Mention which point will have maximum penalty and why?

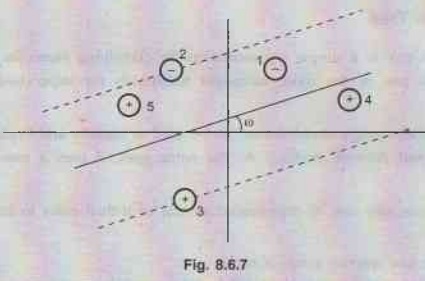
Solution:

• Data points 1 and 5 will have maximum penalty.

• Margin (m) is the gap between data points & the classifier boundary. The margin is the minimum distance of any sample to the decision boundary. If this hyperplane is in the canonical form, the margin can be measured by the length of the weight vector.

• Maximal margin classifier: A classifier in the family F that maximizes the margin. Maximizing the margin is good according to intuition and PAC theory. Implies that only support vectors matter; other training examples are ignorable.

• What if the training set is not linearly separable? Slack variables can be added to allow misclassification of difficult or noisy examples, resulting margin called soft.

• A soft-margin allows a few variables to cross into the margin or over the hyperplane, allowing misclassification.

• We penalize the crossover by looking at the number and distance of the misclassifications. This is a trade off between the hyperplane violations and the margin size. The slack variables are bounded by some set cost. The farther they are from the soft margin, the less influence they have on the prediction.

• All observations have an associated slack variable

1. Slack variable = 0 then all points on the margin.

2.Slack variable > 0 then a point in the margin or on the wrong side of the hyperplane.

3. C is the tradeoff between the slack variable penalty and the margin.