Mathematical Induction

UNIT II: COMBINATORICS

SYLLABUS

Mathematical inductions - Strong induction and well ordering - The basics of counting - The pigeonhole principle - Permutations and combinations - Recurrence relations  - Solving Linear recurrence relations - generating functions - inclusion and exclusion and applications.

Mathematical Induction

The word induction means the method of inferring a general statement from the validity of particular cases. Mathematical induction is a technique by which one can prove mathematical statements involving positive integers.

Principle of Mathematical Induction

Let P (n) be a statement or proposition involving for all positive integrs n. Then we complete two steps.

Basis step: If P (1) is true.

Inductive step: If P (k+1) is true on the assumption that P (k) is true.

Example 1: Prove by induction

1 + 2 + 3 + ….. + n = n(n+1)/2, n ≥ 1.

Solution: Let P (n); 1+ 2+ 3+ ….. + n = n (n + 1)/2, n ≥ 1

Step 1: To prove P(1) is true.

For n = 1, we have

1 = 1(1+1) /2

1 = 1

So P (1) is true.

Step 2: Assume that P (k) is true for any positive integer k.

(i.e.,) 1 + 2 + 3 + ... + k = k (k+1)/2

Step 3: To prove : P (k+1) is true.

(i.e.,) To prove P (k+1) = (k+1) (k+2)/2

[1+2+3+...+k] + k +1 = [k (k + 1)/2] + k + 1

= k (k+1)+2(k + 1)/2

= (k+1) (k+2)/2

= (k+1) [(k+1) + 1]/2

which is P (k+ 1).

That is P (k+1) is true whether P (k) is true.

By the principle of mathematical induction P (n) is true for all positive integer n.

Example 2: Show that 1² + 2² + 3² +...+n² = n(n + 1) (2n + 1)/6, n≥1 by mathematical induction.

Solution: Let P (n): 1² + 2² + 3² + ….. + n² = n (n+1) (2n+1)/6

Step 1: To prove P (1) is true.

For n = 1

1² = 1(1+1) (2+1)/6

1 = 1

So P (1) is true.

Step 2: Assume that P (k) is true.

(i.e.,) 1² + 2² + 3² + …. + k² = k (k+1) (2k+1) /6

Step 3: To prove P (k+1) is true.

 (i.e.,) To prove P (k+1) = (k+1) (k + 2) (2k + 3)/6

[1² + 2² + 3² + ... + k²] + (k+1)² = [ k (k+1) (2k+1)/6 ] + (k+1)²

= k (k + 1) (2k + 1) + 6(k + 1)²/6

= (k + 1) [ 2k² + k + 6k + 6 ]/6

= (k + 1) [ 2k² + 7k + 6 ]/6

= (k + 1) (k + 2) (2k + 3)/6

which is P(k+1).

That is P(k+1) is true whenever P (k) is true.

By the principle of mathematical induction P (n) is true for all positive integer n.

Example 3 Conjecture a formula for the sum of the first n positive odd integers. Then prove by using mathematical induction.

Solution : The sums of the first n positive odd integers for

n = 1, 2, 3, 4, are

1 = 1 = 1²

1+ 3 = 4 = 2²

1 + 3 + 5 = 9 = 3²

1 + 3 + 5 + 7 = 16 = 4²

From these values it is reasonable to conjecture that the sum of the first n positive odd integers is n².

(i.e.,) 1 + 3 + 5+ 7 + ….. + (2n − 1) = n².

Let P (n) 1 + 3 + 5 + ….. + (2n − 1) = n²

Step 1: To prove : P (1) is true.

1 = 1²

So P (1) is true.

Step 2: Assume that P (k) is true.

(i.e.,) 1 + 3 + 5 + ... + (2k − 1) = k²

Step 3: To prove P (k+1) is true.

(i.e.,) To prove P (k + 1) (k + 1)².

[1 + 3 + 5 + …. (2k - 1)] + 2k + 1 = [k²] + 2k + 1

= (k + 1)²

which is P (k+1)

That is P (k+1) is the whenever P (k) is true.

By the principle of mathematical induction P (n) is true.

Example 4: Show that 1/1.2 + 1/2.3 + …. + 1/n(n+1) = n/n+1

Solution: Let P (n): 1/1.2 + 1/2.3 + …. + 1/n(n+1) = n/n+1

Step 1: To prove P (1) is true.

(i.e.,) 1/1.2 = 1/1+1

½ = ½

Hence P (1) is true.

Step 2: Assume that P (k) is true.

 (i.e.,) 1/1.2 + 1/2.3 + …. + 1/k(k+1) = k/k+1

Step 3: To prove P (k+1) is true.

(i.e.,) P (k+1) = k+1/ (k+1)+1 = k+1/ k+2

[1/1.2 + 1/2.3 + …. + 1/k(k+1)] + 1 / (k+1) (k+2) = [ k/k+1] + [ 1/(k+1)(k+2) ]

= k(k+2)+1 / (k+1)(k+2)

= k²+2k+1 / (k+1)(k+2)

= (k+1)² / (k+1)(k+2)  = k+1 / k+2

which is P (k+1)

That is P (k+1) is true whenever P (k) is true.

By the principle of mathematical induction P (n) is true.

Example 5: Prove by mathematical induction that 2ⁿ > n for all n ϵ N. (or) n < 2ⁿ for all positive integers n. [A.U N/D 2012]

Solution: Let P (n): n < 2ⁿ

Step 1: To prove P (1) is true. 1 < 2¹

⇒ 1 < 2

Hence P (1) is true.

Step 2: Assume that P (k) is true.

(i.e.,) k < 2^k

Step 3: To prove : P (k+1) is true

 (i.e.,) To prove : P (k + 1) = 2^k+1

(i.e.,) k < 2^k

⇒ k + 1 < 2^k+1

⇒ k + 1 < 2^k + 2^k       ['.' 1 ≤ 2^k]

⇒ k + 1 < 2 (2^k)

⇒ k + 1 < 2^k +1

which is P (k + 1)

That is P (k+1) is true whenever P (k) is true.

Example 6: Show that aⁿ - bⁿ is divisible by (a - b) for all, n Є N

Solution: Let P (n) (aⁿ - bⁿ) is divisible by (a - b)

Step 1: To prove P (1) is true.

(a¹ - b¹) = (a - b) is divisible by (a - b)

Hence P (1) is true.

Step 2: Assume that P (k) is true.

Let (a^k - b^k) = c (a - b)

⇒ a^k = b^k + c (a - b) ... (1)

Now   a^k+1 - b^k+1 = a^ka – b^kb

= a[ b^k + c (a - b)] - b^kb by (1)

= ab^k + ac (a - b) - b^kb

= b^k (a - b) + ac (a - b)

= (a - b) (b^k + ac)

which is divisible by (a - b)

(ie.,) That is P (k+1) is true whenever P (k) is true.

By the principle of mathematical induction,

P (n) is true for all n Є N.

Example 7: Prove the formula for the sum of first n cubes using the mathematical induction.

S_n = [ n(n + 1)/2]²

Solution: Let P (n) : 1³ + 2³ + …. + n³ =  [ n(n + 1)/2]²

Step 1: To prove P (1) is true.

1³ =  [ 1(1 + 1)/2]

1 = 1

Hence P (1) is true.

Step 2: Assume that P (k) is true.

(i.e.,) 1³ + 2³ + …. + k³ =  [ k(k + 1)/2]²

Step 3: To prove : P (k + 1) is true.

That is P (k+1) is true whenever P (k) is true.

Example 8: If A₁, A₂ …. A_n are any n sets, show by mathematical induction that  

Solution : Let P (n) be the statement that the equality holds for n sets.

Step 1: To prove P (1) is true.

Hence P (k+1) is true.

So by the principle of mathematical induction P (n) is true for all n ≥ 1.

Example 9: Sums of Geometric progressions : Prove that a + ar + ar² +….+ arⁿ = arⁿ⁺¹ - a / r-1; r ≠ 1 by mathematical induction, where n is a non negative integer.

Solution: Let P (n): a + ar + ar² +….+ arⁿ = arⁿ⁺¹ - a / r-1

Step 1: To prove P (0) is true.

a = ar-a / r-1

= a.

Hence P (0) is true.

Step 2: Assume that P(k) is true.

Hence P (k+1) is true.

So by the principle of mathematical induction P(n) is true for all non-negative integers.

Example 10: Use mathematical inductin to show that H₂ⁿ ≥ 1+ n/2 whenever n is a non-negative integer.

Solution: Let P (n): H₂ⁿ ≥ 1+ n/2

Step 1: To prove P (0) is true.

H₂⁰ = H₁ = 1 ≥ 1+ 0/2      [H₄ = 1 + ½ + 1/3 + ¼ ]

Hence P (0) is true.

Step 2: Assume that P (k) is true.

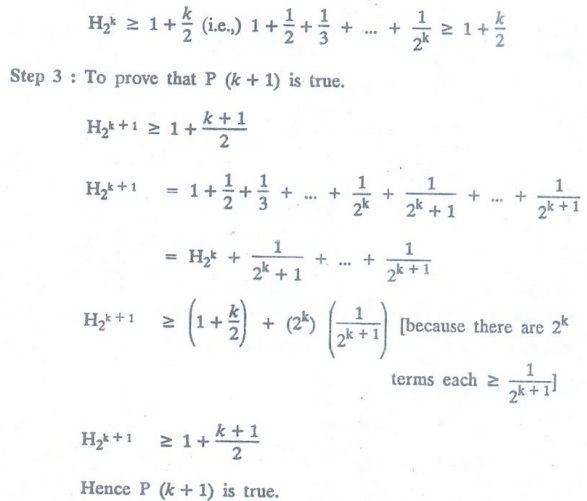
Hence P (k+1) is true.

This establishes the inductive step of the proof.

Example 11: Use mathematical induction to show that 2ⁿ <n! for every positive integer n with n ≥ 4.

Solution: Let P (n): 2ⁿ < n!, n ≥ 4

Step 1: To prove P (4) is true.

(i.e.,) 2⁴ < 4!

⇒ 16 < (1, 2, 3, 4)

⇒ 16 < 24

Hence P (4) is true.

Step 2: Assume that P (k) is true.

(i.e.,) 2 <k!, k ≥ 4

Step 3: To prove P (k+1) is true.

(2^k) 2 < 2 (k!)

2^k+1 < (k!) (k + 1)      [ 2 < (k + 1)]

2^k+1 < (k+1)!

Hence P (k+1) is true.

This completes the inductive step of the proof.

Example 12: Use mathematical induction to prove that n³ - n is divisible by 3 whether n is a positive integer.

Solution: Let P (n) : (n³ – n) is divisible by 3.

Step 1: To prove P (1) is true.

1-1= 0 is divisible by 3.

Hence P (1) is true.

Step 2: Assume that P (k) is true.

(i.e.,) (k³ – k) is divisible by 3.

Step 3: To prove P (k+1) is true.

(i.e.,) To prove (k + 1)³ − (k + 1) is divisible by 3.

(k + 1)³ - (k + 1) = (k³ + 3k² + 3k + 1) − (k + 1)

= (k³ −k) + 3(k² + k)

which is divisible by 3.

Hence P (k+1) is true.

This completes the inductive step.

EXERCISE 2.1

1. Use mathematical induction to show that n! ≥ 2^n-1 for n = 1, 2, 3...

12. 3ⁿ <n!, n>6

13. (n² + n) is divisible by 2, n is a positive integer.

14. (n⁵ - n) is divisible by 5, n is a positive integer.

15. (n³ - n) is divisible by 6, n is a positive integer.