Magnitude Comparator

Magnitude Comparator 

AU: Dec.-14, May-07,08,11,19

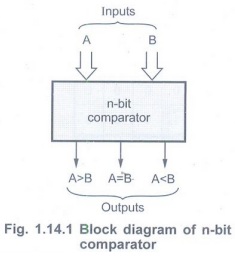
A comparator is a special combinational circuit designed primarily to compare the relative magnitude of two binary numbers. Fig. 1.14.1 shows the block diagram of an n-bit comparator. It receives two n-bit numbers A and B as inputs and the outputs are AB, A = B and A < B. Depending upon the relative magnitudes of the two number, one of the outputs will be high.

Example 1.14.1 Design 2-bit comparator using gates.  AU Dec.-14, Marks 8

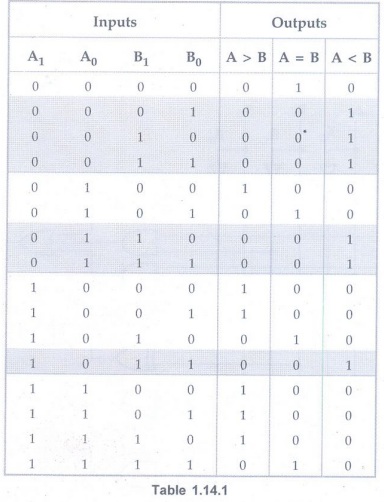
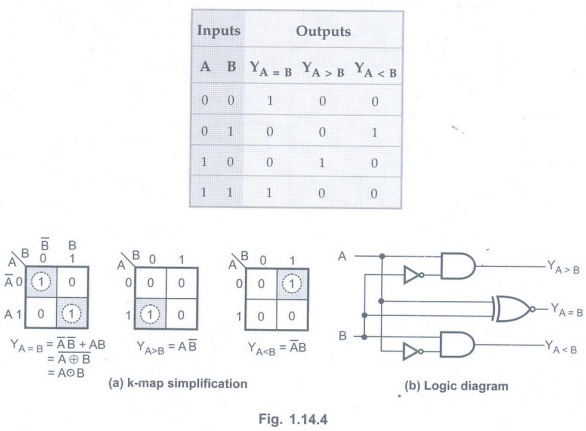
Solution: The truth table for 2-bit is given in Table 1.14.1.

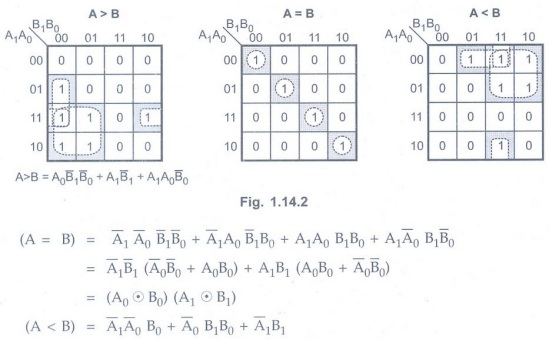
K-map simplification

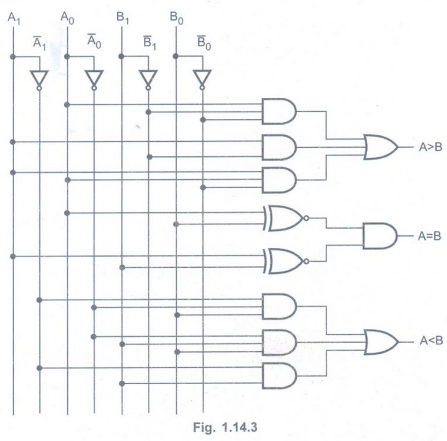
Logic diagram

Example 1.14.2 Design a 1-bit comparator using basic gates. AU May-11, Marks 2

Solution: Consider two one bit number A and B. The truth table is as shown.

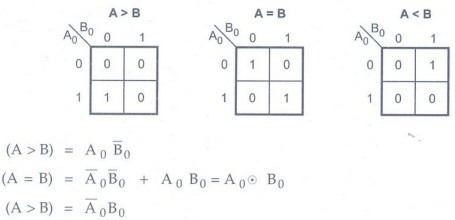
4-bit Magnitude Comparator

Consider two binary numbers, A and B with four digits each.

A = A₃, A₂, A₁, A₀

 and B = B₃, B₂, B₁, B₀

When the numbers are binary, the digits are either 0 or 1, and the equality of each pair of bits can be expressed logically with an exclusive-NOR function as

x_i = A_i B_i +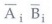

for i = 0, 1, 2, 3

where x_i = 1 only if the pair of bits in position i are equal. This can be expressed as

(A = B) = x₃, x₂, x₁, x₀

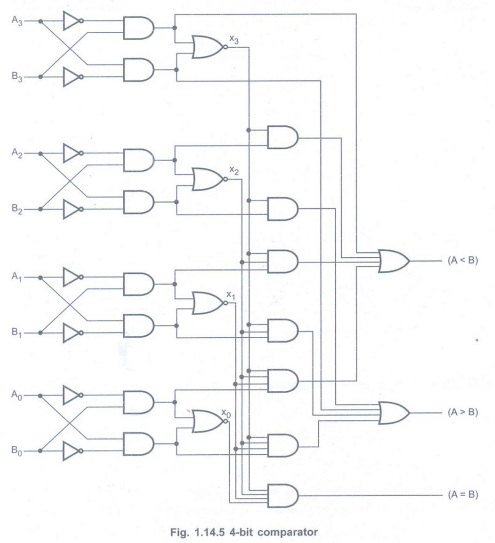
To determine whether A is greater or less than B, we check the relative magnitudes of pairs of significant digits, starting from the most significant position. If the two digits of a pair are equal, we compare the next lower significant pair of digits. The comparison continues until a pair of unequal digits is reached. If corresponding digit of A is 0 and that of B is 1, we can say that A < B. If the corresponding digit of A is 1 and that of B is 0, we can say that A > B.

The above sequential comparison can be expressed logically by the two Boolean functions.

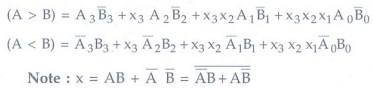
IC 7485 (4-bit Comparator)

IC 7485 is a 4-bit comparator. It can be used to compare two 4-bit binary words by grounding I (A < B), and I (A > B), and connector input I (A = B) to V_cc. These ICs, can be cascaded to compare words of almost any length. Its 4-bit inputs are weighted (A₀ – A₃) and (B₀ – B₃), where A₃ and B₃ are the most significant bits.

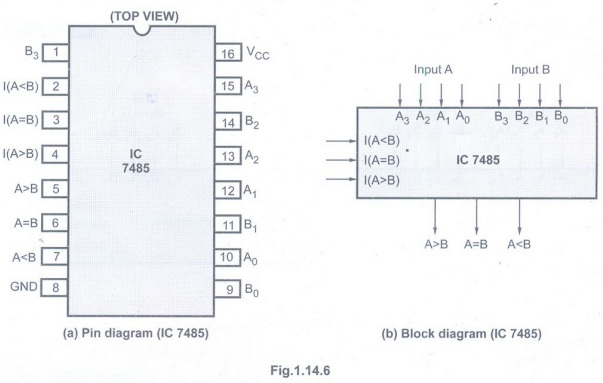
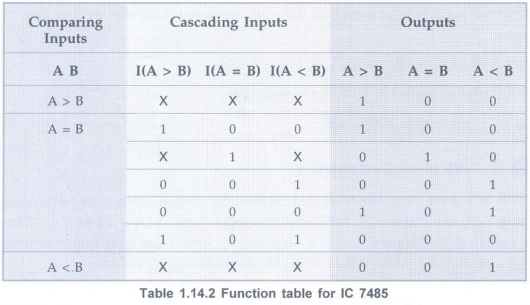
Fig. 1.14.6 shows the logic symbol and pin diagram of IC 7485. The operation of IC 7485 is described in the function table, showing all possible logic conditions.

Example 1.14.3 Design an 8-bit comparator using two 7485 ICs. AU: May-07

Solution :Fig. 1.14.7 shows an 8-bit comparator using two 7485 ICs.

Example 1.14.4 Design a 5-bit magnitude comparator using comparator IC 7485.  AU May-08, Marks 8

Solution: Truth Table

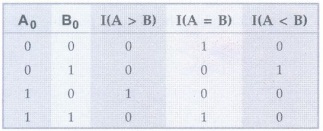
K-map Simplification

Implementation

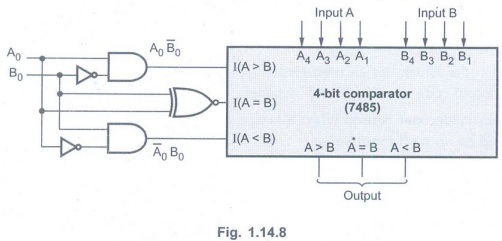
Examples for Practice

Example 1.14.5 Design a 4-bit magnitude comparator to compare two 4-bit numbers.  AU May-19, Marks 7

Example 1.14.6 Explain comparison of n-bit binary numbers.

Review Question

1. Draw the schematic of a magnitude comparator and give its truth table.  AU: May-11, Marks 6