Logical Equivalences and Implications - De Morgan`s Laws

LOGICAL EQUIVALENCES AND IMPLICATIONS - De MORGAN'S LAWS

Compound propositions that have the same truth values in all possible cases are called logically equivalent.

16 different truth tables of compound propositions involve the propositions P and Q.

Definition: The propositions P and Q are called logically equivalent if P Q is a tautology.

Note: The notation P = Q denotes that P and Q are logically equivalent. (or) We use P <->Q also.

Example 1: Show that P is equivalent to the following formulae.

(i) ┐┐P

(ii) P^ P

(iii) P V P

(iv) PV (P^  Q)

(v) P^  (PV Q) [MCA, 1996, M.U]

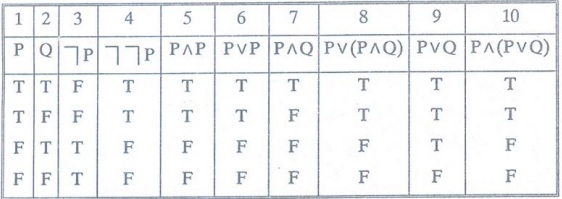
Here the 4th, 5th, 6th, 8th, 10th columns give the truth values of the formulas. The columns 1, 4, 6, 8, 10 have the identical truth values. Hence P is equivalent to all the given formulas.

Example 2 : Show that P is equivalent to the following formulas.

(i) (PɅ Q) V (PɅ ┐Q)

(ii) (P VQ) Ʌ (PV ┐Q) [MCA, M.U May, 1995]

Solution :

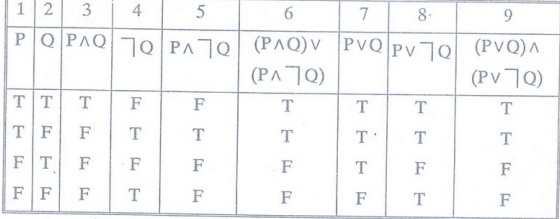
Columns 1, 6, 9 have identical truth values.

Hence P↔ (P^Q) V (P^┐Q)

↔ (PVQ)^(PV┐Q)

Example 3: Show that the propositions are logically equivalent.

P →Q and ┐PV Q

Solution :

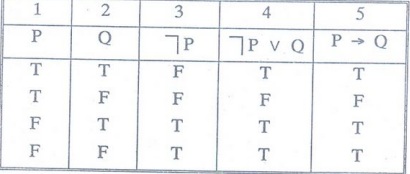
Columns 4 and 5 have identical truth values. Hence ┐PVQ↔P→Q.

Example 4: Show the following equivalences.

(a) ┐ (P ^ Q) ↔ ┐P v ┐Q

 (b) ┐ (P v Q) ↔ ┐р^ ┐Q

(c) ┐ (P → Q) ↔ P ^┐Q

(d) ┐ (P ↔ Q) ↔ (P ^┐Q) V (┐P ^ Q)                       

Solution :

(a) Column 6 and 9 are equal.

┐ (P^ Q) ┐↔ P v ┐Q

 (b) Column 8 and 10 are equal.

┐ (P VQ) ↔ ┐р ^ ┐Q

(c) Column 12 and 13 are equal.

┐ (P->Q) ↔ (P ^ ┐Q)

(d) Column 15 and 17 are equal

┐ (P ->Q) ↔ (P ^ ┐Q) v (┐р^ Q)

Table logic equivalences

Replacement Process

Consider the formula A: P→ (Q → R)

Here Q →R is a part of the formula A.

If we replace Q→R by an equivalent formula ┐QVR in A, we get another formula

B: P→ (┐QVR). We can easily verify that the formulas A and B are equivalent to each other.

This process of obtaining B from A is known as the replacement process.

Tautological Implications

A statement A is said to tautologically imply a statement B if and only if A → B is a tautology. In this case, we write A ⇒ B, read as "A implies B".

Table Implications

1. P^Q ⇒ P

2. P^Q⇒Q

3. P ⇒ P V Q

4. ┐ P⇒P → Q

5. Q ⇒ P→ Q

6. ┐ (P →> Q) ⇒ P

7. ┐ (P → Q) ⇒┐Q

8. P^ (Р → Q) = Q

9. ┐Q ^ (Р→Q) ⇒ ┐P

10. ┐p ^ (P v Q) ⇒ Q

11. (P →Q) ^ (Q →R) ⇒ P→R

12. (P v Q) ^ (P→R) ^ (Q→R) ⇒ R

Example 1: Show that (┐P^(┐Q^R)) v (Q^R) v (P^R) ↔ R [A.U. N/D, 2003]

Solution :

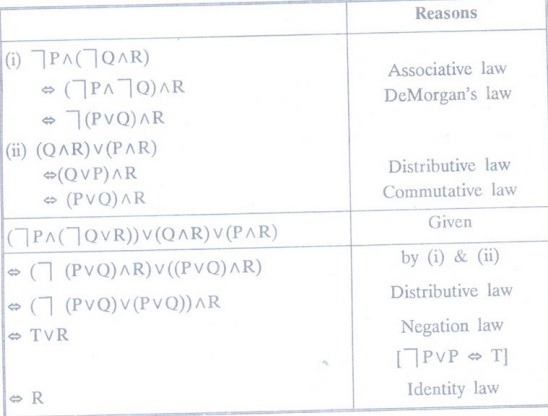
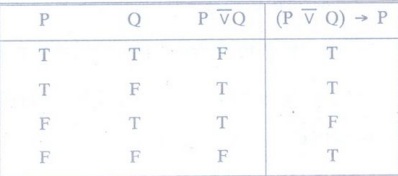
Example 2: Show that (PVQ) ^ ┐(┐P^Q) → P

Solution :

Example 3 : Show that ┐ [┐ [[P v Q] ^ R] v ┐Q] ↔ Q ^ R.

Solution :

Example 4: Simplify the statement using the laws of logic (PVQVR) A (P v T V ┐Q) ^ (P v┐T v R)

Solution :

Example 5: Show that ┐ (P v (┐P^Q)) and ┐P ^ ┐Q are logically equivalent.

Solution :

Consequently, ┐ (P v (┐P^Q)) and ┐P ^ ┐Q are logically equivalent.

Example 6: Show that ┐ (P^Q)→( ┐Pv(┐PvQ)) ↔ (┐PvQ)

(use only the laws) [A.U. A/M 2004]

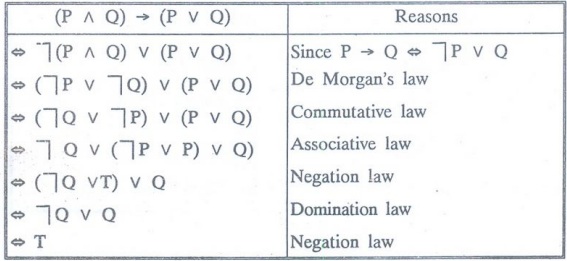
Example 7: Show that (P^Q) → (P v Q) is a tautology.

Solution :

Example 8 : Show that (P V Q) Ʌ ┐P ↔ ┐P ^ Q.

Solution :

Example 9: Show that (PVQ) Ʌ (┐P^(┐P^Q)) ↔  (┐P^Q) [MCA, M.U May, 1995]

Solution :

Example 10: Show that ((P v Q) ^ ┐ (┐P ^ (┐Q v ┐R))) V (┐P ^ ┐Q) v (┐P^┐R) is a tautology.

Solution :

┐P ^ ┐Q  ↔ ┐(P v Q) De Morgan's law

┐P ^ ┐R  ↔ ┐(P v R) De Morgan's law

(i) (┐P ^ ┐Q) v (┐P^┐R) ↔ ┐(P v Q) v ┐(P v R)  ↔ ┐((P v Q) ^ (P v R)) De Morgan's law

Also

(ii) ┐ (┐P ^ (┐Q v ┐R))

┐ (┐P v ┐(Q v R)) De Morgan's law

P v (Q ^ R)      since ┐(P ^ R) ↔ ┐P  v ┐R 

(P v Q) ^ (P v R) Distributive law

from (i) and (ii) we get

((P v Q) ^ (P v R) v ┐((P v Q) ^ (P v R))

↔ T           [P v ┐P↔ T]

Example 11: Show that P→(Q→R) ↔ (P^Q)→R ↔ P→(┐Q v R) [MCA, MU Dec, 92, May, 93, Nov., 94, May, 95]

Solution :

Example 12: Show that P→ (Q→P) ↔ ┐P → (P→Q) [MCA, M.U May, 1995]

Solution :

from (i) and (ii) we get P→ (Q→P) ↔ ┐P→ (P. → Q)

Example 13 : Show that P → (Q v R) ↔ (P →Q) V (P→R) [M.C.A, M.U, May 1995]

Solution :

Example 14: Show that (P →Q) Ʌ (R → Q) ↔ (PVR) → Q. [MCA N/D 2002]

Solution :

Example 15: Show that  ┐ (P↔Q) ↔ (P v Q) Ʌ ┐(P Ʌ Q).

Solution :

Tautological Implications

A statement A is said to tautologically imply a statement B if and only if AB is a tautology. In this case, we write A ↔ B, read as "A implies B".

Example 1: Show that (P ^ Q) => (P Q).

Solution To prove (P ^ Q) → (P → Q) is a tautology.

Example 2: Show the following implication P⇒ (Q→P)

Solution : To prove P→ (Q→P) is a tautology.

Example 3 : Show that the following is an implication.

(P → (Q→R) ⇒ (P→ Q)→(P→R).

Solution : To prove (P → (Q→R)→ (P→ Q)→(P→R) is a tautology.

Example 4: Show that the following formula is an implication.

P → Q ⇒ P→ (PɅ Q)

Solution :  Reason

(i) P→ (PɅ Q)

↔ ┐P v  (P Ʌ Q) since P → Q ⇒ ┐P V Q

↔ (┐P V P) Ʌ (┐P v Q)

↔ T Ʌ (┐P v Q)

↔ ┐P v Q

 (ii) (P→ Q) → (┐P v Q)

↔ (┐P V Q) →  (┐P v Q)

↔ ┐ (┐P V Q) →  (┐P v Q)

↔ T

(P → Q) → (P → (P v Q)

Example 5: Show that the formula is an implication.

(P → Q)  → Q ⇒ P V Q

Solution : To prove : ((P → Q) → Q) → (PV Q) is a tautology.

 (i) (P → Q) → Q  Reason

↔ ┐ (P → Q) v Q   since P→ Q ↔ ┐P V Q

↔ ┐ (┐P v Q) v Q  since P→ Q ↔ ┐P V Q

↔ (┐ (┐P )^ ┐Q) v Q  since P→ Q ↔ ┐P V Q

 ↔ (P ^ ┐Q) v Q  since P→ Q ↔ ┐P V Q

↔ (P v Q) ^ (7Q v Q)  Distributive law

↔ (P V Q) ^ T  Negation law

↔ P V Q  Identity law

(ii) (P v Q) → (P V Q) Reason

↔ ┐(P v Q) V (P v Q)   since P→ Q ↔ ┐P V Q

↔ T     ┐P V P ↔ T

Hence the proof.

Example 6 : Show that the given formula is an implication ((P v ┐Q) → Q) → ((P v ┐P) → R) ⇒ (Q → R)

Solution : To prove ((P v ┐Q) → Q) → ((P v ┐P) → R) ⇒ (Q → R) is a tautology.

(i) (P v ┐Q) → Q Reason

↔  ┐ (P v ┐ Q) v Q  since P → Q  ┐P VQ

↔  (┐P ^ ┐(┐Q)) v Q  De Morgan

↔ (┐P ^ Q) V Q  Double negation

↔ (┐P V Q) ^ (Q V Q) Distributive law

↔ (┐PV Q) ^ Q Idempotent law

 (ii) (Pv┐P) → R Reason

T→R  Negation law

↔ ┐T V R      P → Q↔ ┐P VQ

↔ ┐ (TɅ ┐R)  De Morgan

↔ ┐(T)   Dominative law

↔ F

(iii) ((┐(P v Q) ^ Q) → F

↔ ┐ ((┐P v Q) ^ Q) V F

↔ (┐ (┐ P V Q) v ┐Q) v F

↔ ((┐ (┐P) ^ ┐Q) v ┐Q) v F

↔ ((P ^ ┐Q) v 7Q) v F

(iv) ((P Ʌ ┐Q) v ┐Q) v F→ (Q→ R)

↔┐((P Ʌ ┐Q) v ┐Q) v F) v (┐Q v R)

↔ (┐((P Ʌ ┐Q) v ┐Q)  Ʌ ┐F) v (┐Q v R)

↔ ((┐P V ┐ (┐Q)) v ┐Q)  Ʌ T) v (┐Q v R)

↔ (┐P v Q) v ┐Q v (┐Q v R)

↔ (┐P v (Q v ┐Q) v (┐Q v R)

↔ (┐P v T) v (┐Q v R)

↔ T v (┐Q v R)

↔ T

Hence the proof.

 Theorem 1 :

If H₁, H₂, … H_m and P imply Q, then

H₁, H₂ ... H_m imply P → Q

Proof: Given (H₁ ^  H₂ ^ ... ^ H_m ^ P) ⇒ Q

 (i.e.,) (Н₁ ^  Н₂ ^ … ^  H_m ^  P)→ Q is a tautology.

↔ (Н₁ ^ Н₂ ^ … Ʌ H_m) → (P→Q) is also a tautology.

since (P^Q) → R ↔ P→ (Q → R)

(Н1 ^ Н2 ^  ... ^  H_m) ↔ (P → Q)

Duality

The dual of a compound proposition that contains only the logical operators v, ^ and ┐ is the proposition obtained by replacing each v by  ^  , each  ^  by v, each T by F and each F by T. The dual of proposition A is denoted by A*.

Examples

(i) The dual of (P ^ ┐Q) v R is (P v ┐Q) ^ R

(ii) The dual of (T v P) ^ Q is (F^ P) v Q

(iii) The dual of (P → Q) Ʌ (R V F) ↔ (┐P v Q) ^ (RV F) is (┐P ^ Q) V (R ^ T)

Theorem 2: Duality principle theorem

If A and A* be dual formulas and if P₁, ….P_n be the atomic variables that occur in A and A*

(i.e.,)

A = A (P₁, ... P_n) and A* = A *(P1, P2, ... Pn) then

┐A (P₁,… P_n) ↔ A* (┐P₁, ... P_n) and

A (┐P₁, ... ┐P_n) ↔ ┐A* (P₁, ... P_n)

That is the negation of a formula is equivalent to its dual in which every variable is replaced by its negation.

Note: If any two formulas A and B are equivalent, then their duals A* and B* are also equivalent.

Example 1: Write the equivalent form of

A (P, Q, R) ↔ P V (┐QɅR)

The dual of A (P, Q, R) is

A* (P, Q, R) = PɅ (┐Q VR)

A* (┐P, ┐Q, ┐R) = ┐PɅ (Q V ┐R)

↔ ┐A (P, Q, R) ↔  ┐ (P v ┐Q ^ R)

↔ ┐PɅ (Q V ┐R)

Hence ┐A (P, Q, R) ↔ A* (┐P, ┐Q, ┐R)

Example 2 : Show that A↔B  if and only if A* ↔ B*

Solution: Let A (P₁, P₂, …. P_n) ↔ B (P₁, P₂, ... P_n)

Then A(P₁, P₂, … P_n) ↔ B (P₁, P₂, ... P_n) is a tautology.

A (┐P₁, ┐P₂, ... ┐P_n) ↔ B (┐P₁, ┐P₂, ... ┐P_n)  is a tautology.

By duality principle theorem

┐A* (P₁, P₂, …. P_n) ↔ ┐B* (P₁, P₂, ... P_n) is a tautology.

┐A*↔ ┐B*

Hence A* ↔ B*.

Functionally complete sets of connectives [A.UA/M 2005]

Any set of co^ectives in which every formula can be expressed as another equivalent formula containing connectives from this set is called functionally complete set of connective.

(or)

 A collection of logical operators is called functionally complete if every compound proposition is logically equivalent to a compound proposition involving only these logical operators.

Example :

The set of connectives { Ʌ, ┐} and {V, ┐} are functionally complete.

{┐}, { Ʌ }, {V} or {V, Ʌ } are not functionally complete.

Note: From the five co^ectives Ʌ, V, ┐, →, ↔ we have obtained atleast two sets of functionally complete co^ectives.

Example 1: Write an equivalent formula for P Ʌ (Q↔R) V (R↔P) which does not contain the biconditional.

Solution :

P Ʌ (Q↔R) V (R ↔P)

↔P Ʌ  ((Q→R) Ʌ (R→ Q)) V ((R→P) Ʌ (P→ R))

Thus the equivalent formula is

P Ʌ ((Q→R) Ʌ (R →Q)) V ((R→P) Ʌ (P→R))

Example 2: Write an equivalent formula for P Ʌ (Q↔R) which contains neither the biconditional nor the conditional.

Solution :

P Ʌ (Q↔R) P Ʌ ((Q→R) Ʌ (R →Q))

↔P Ʌ ((┐Q V R) Ʌ (┐R v Q))

Thus the required formula is P Ʌ ((┐Q V R) Ʌ (┐R v Q))

Example 3 : Prove that {┐, v} is a functionally complete set of connectives.

Solution

To prove {┐, v} is a functionally complete set of coɅectives, we have to show for all formulas with other coɅectives, there exists a equivalent formula which contains ┐ and V only.

For example

P↔Q  ↔ (P→Q) Ʌ (Q → P)

↔ (┐PVQ) Ʌ (┐Q V P)

P→Q  ↔ ┐P VQ

P Ʌ Q ↔ ┐(┐P v ┐Q)

If we apply the above three equivalent rules in the given formula, then the resultant is free from biconditional, conditional and conjunction.

[First replace all the biconditionals, then the conditionals and finally are conjunctions.]

Hence {┐, v} is a functionally complete set of connectives.

Note: In the same way we have to prove {┐, ^} is a functionally complete set of connectives.

Example 4: Show that {V, A} is not functionally complete.

[A.U. N/D 2004]

Solution : ┐ caɅot be expressed using the connectives {V, Ʌ }. Since no such contribution of statement exist with {V, Ʌ } as input is T and the output is F.

THE OTHER CONNECTIVES

Exclusive OR

Table

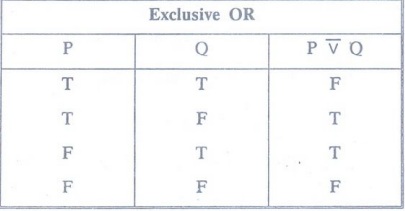
The following equivalences follow from its definition.

NAND (↑)

"NAND" is a word which is a combination of the words "NOT" and "AND" when NOT stands for negation and "AND" stands for conjunction. It is denoted by the symbol "↑ ".

Let P and Q be any two statement formulas, then "P NAND Q" is denoted by "P ↑ Q" and is defined as P ↑ Q

♦ NOR (↓)

The word "NOR" is a combination of "NOT" and "OR" where NOT stands for negation and "OR" stands for disjunction. It is denoted by "↓".

Let P and Q be any two statement formulas, then "P NOR Q" is denoted by "P↓Q" and is defined as P↓Q ↔ ┐(P v Q).

Some basic properties of NAND and NOR.

1. P ↑ Q ↔ Q ↑ P, P↓ Q ↔ Q ↓ P (commutative)

2. P ↑ (Q ↑ R) ↔ P ↑ ┐ (Q Ʌ R)

↔  ┐(P ^ ┐ (Q ^ R))

↔ ┐PV (Q Ʌ R)

(P ↑ Q) ↑ R ↔ (P Ʌ Q) V ┐R (not associative)

Similarly, P ↓ (Q↓R) also not associative.

Note: The operators ↑ and ↓ are called the sheffer stroke and the pierce arrow after H.M. Sheffer and C.S. Peirce, respectively.

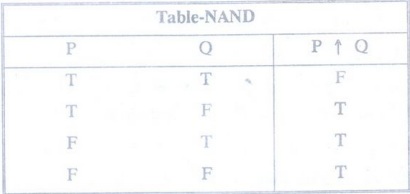
Example 1: Construct the truth table for NAND.

Solution :

Example 2: Construct the truth table for "NOR".

Solution :

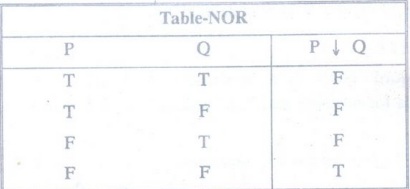
Example 3: Construct the truth table for

Example 4: Show that (i) (P ↑ Q) ↔ ┐P↓ ┐Q

(ii) ┐ (P↓Q) ↔ ┐P ↑ ┐Q

Solution: (i)(P. ↑ Q) ⇔ ┐ (┐ (P Ʌ Q))

⇔р Ʌ Q ……… (1)

┐P  ↓  ┐Q ⇔ ┐ (┐ (P v ┐Q))

⇔ ┐ ┐P Ʌ ┐ ┐ Q by De Morgan's law

⇔ P Ʌ Q ………..(2)

From (1) and (2) we get

(P ↑ Q) ↔ ┐P↓ ┐Q

(ii) ┐ (P↓Q) ⇔ ┐ (┐ (P v Q))

 ⇔ P v Q ………..(3)

and  ┐P ↑ ┐Q ⇔ ┐ (┐ (P  Ʌ ┐Q))

⇔ ┐ ┐P v ┐ ┐Q

⇔ P V Q ………..(4)

Hence ┐ (P↓Q) ⇔ ┐P ↑ ┐Q by (3) and (4).

Example 5: Express P ↑ Q interms of  ↓ only.

Solution: P ↑ Q ⇔ ┐ (P ^ Q)

⇔┐P v ┐Q

⇔ (P↓P) V (Q ↓ Q)    [(P↓P) ⇔ ┐ P]

⇔  [(P↓P) ↓  (Q ↓ Q) ]  ↓ [ (P↓P) V (Q ↓ Q) ] 

Example 6 : Express P → (┐P → Q) interms of ↑ only.

Proof : P → (┐P → Q) ⇔  ┐P v (┐P → Q)

⇔  ┐P v (┐┐P v Q)

⇔  ┐P v (P v Q)

⇔  (┐P v P )v Q

⇔ T v Q

⇔ (T ↑ T) ↑ (Q ↑ Q)

Example 7: Prove that {↑ } and ↓ are functionally complete sets of coɅectives. They are also known as minimal functionally complete set.

Solution: In order to prove, it is sufficient to show that the sets of co^ectives {A, ┐} and {v, ┐} can be expressed either in terms of ↑ alone or in terms of ↓ alone.

I: To prove ↑ is a functionally complete set.

(i) ┐P  ⇔  ┐P v ┐P

⇔  ┐(P Ʌ P)

⇔ P ↑ P ……(1)

(ii) PɅ Q ⇔ ┐ (P ↑ Q)

⇔ (P ↑ Q) ↑ (P ↑ Q) ……(2)

 (iii) P V Q ⇔ ┐(┐P Ʌ ┐Q)

⇔ ┐P ↑ ┐Q

 (P ↑ P) ↑ (Q ↑ Q) ……..(3)

By (1), (2) and (3) ↑ is a functionally complete set.

II. To prove is a functionally complete set.

(i) ┐P  ⇔ ┐P ^ ┐P

⇔  ┐ (P v P)

⇔ P ↓ P ……...(1)

(ii) P V Q  ⇔ ┐(P↓Q)

(P↓ Q) ↓ (P↓ Q) …….(2)

(iii) P^Q   ⇔ ┐P ↓ ┐Q

(P↓P) ↓ (Q ↓ Q) ..….(3)

By (1), (2) and (3) we get {↓} is a functionally complete set.

EXERCISE

I. Prove that the following equivalences.

1. P→Q ↔ ┐P VQ

2. PV (P^Q) ↔ P

3. P→ (Q→R) ↔ P→ (┐Q v R).

4. (P→Q) ^ (R →Q) ↔ (P v R) → Q

5. (P^Q) → R ↔ (P→R) V (Q → R)

6. ┐(P ⇔ Q) ↔ (P ^ ┐Q) V (┐         P ^ Q)

II. Show that implications without constructing the truth tables.

1. ┐(P ^ Q) → (┐P v (┐P v Q)) → ┐P v Q

2. ┐ (P→Q) → P

3. P ^ (P→Q) => Q

4. (P→ (Q→R)) => (P → Q) → (P→R)

5. ┐Q ^ (Р →Q) => ┐P

6. (P v Q) ^ (┐P) =>Q

7. P → Q => P → (P ^ Q)

8. (P →Q) → Q => P VQ

9. (Q → (P ^ ┐P)) → (R→ (P ^ ┐P) ⇒ (R → Q)

10. ((P v ┐P) → Q) v ((P v ┐P) →R) => (Q→R)

11. Q => P → R

12. (P ^ Q) => P→ Q

III. Show that

(i)  ┐ (P↓ Q) => ┐P ↑ ┐Q

(ii) ┐ (P↓Q) => ┐P ↓ ┐Q)

IV. Show that (┐P ^ (┐Q ^ R)) V (Q ^ R) V (P ^ R) => R

****