Logical Connectives

LOGICAL CONNECTIVES – COMPOUND PROPOSITIONS - CONDITIONAL AND BICONDITIONAL PROPOSITIONS - TRUTH TABLES.

The area of logic that deals with propositions is called the propositional calculus or propositional logic.

FIVE BASIC CONNECTIVES

Molecular [compound] [composite] statements

Definition :

Molecular (compound) (composite) statements

New statements can be formed from atomic statements through the use of connectives such as 'and', 'but', 'or' etc. The resulting statements are called molecular or compound statements.

Example :

Niranjan is a boy and Sita is a girl.

Note : Atomic statements do not contain connectives.

Definition :

• Compound propositions :

Many mathematical statements are constructed by combining one or more propositions, new propositions, called compound propositions, are formed from existing propositions using logical operators.

Definition: Truth Table

A table, giving the truth values of a compound statement interms of its component parts, is called a "Truth table'.

Note: A 'Truth table' displays the relationships between the truth values of propositions. Truth tables are especially valuable in the determination of the truth values of propositions constructed from simpler propositions.

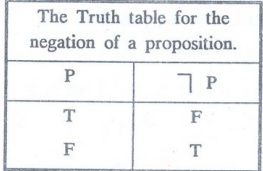
Definition: Negation [┐ or ~] [Not]

The negation of a statement is generally formed by introducing the word 'not' at a proper place in the statement.

If 'P' denotes a statement, then the negation of P is written as `┐p' and read  as 'not P'.

If the truth values of P is T, then

the truth value of  ┐ p is. F.

Also the truth value of P is F, then

the truth value of  ┐ p is T.

Table 1

Example 1: P: To day is Monday [True]

┐ p: Today is not Monday. [False]

Example 2: P: x<y

┐ p: x not < y or x ≥ y

Example 3: P: 3<2 [False]

┐ p: 3 > 2 [True]

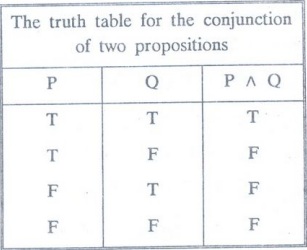
Definition: Conjunction [^] [AND]

The conjunction of two statements P and Q is the statement P˄Q which is read as "P and Q".

The statement P˄Q has the truth value T whenever both P and Q have the truth value T; otherwise it has the truth value F.

Table 2

Example 1: P: It is snowing [True]

Q: I am cold [True]

P ^ Q: It is snowing and I am cold [True]

Example 2: P: 4+3<5 [False]

Q : -3>-5 [True]

P ^ Q : 4+3<5 and -3> - 5 [False]

Example 3: P : 2 < 6 [True]

Q : 2+6 = 9 [False]

P ^ Q : 2<6 and 2 + 6 = 9 [False]

Example 4: P: 3+5 = 6 [False]

Q : 3 – 5 = 4 [False]

Р ^ Q : 3 + 5 = 4 and 3 – 5 = 4 [False]

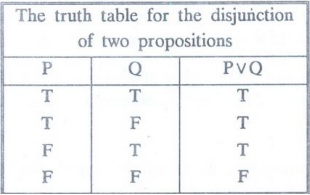
Definition: Disjunction [V] [or]            

The disjunction of two statements P and Q is the statement PVQ which is read as "P or Q".

The statement PVQ has the truth value F only when both P and Q have the truth value F; otherwise it is true.

Table 3

Example 1: P : 2 is a positive integer. [True]

Q : √2 is a rational number [True]

P ˅ Q 2 is a positive integer or √2 is a rational number. [True]

Example 2 : P : 2+3 = 5 [True]

Q : 3<2 [False]

P ˅ Q : 2 + 3= 5 or 3 < 2 [True]

Example 3 : P : 3+4 = 6 [False]

Q : London is the capital of India [False]

P ˅ Q: 3 + 4 = 6 or London is the capital of India.[False]

Note:

1. I left for India on Monday or I left for India on Friday. Exactly one of the two possibilities could have occurred. So the connective or is being used in an exclusive sense.

2. I passed mathematics or I failed science. In this case, atleast one of the two possibilities occured. So the connective or is being used in an inclusive sense.

3. In mathematics and computer science we agree to use the connective or always in the inclusive manner.

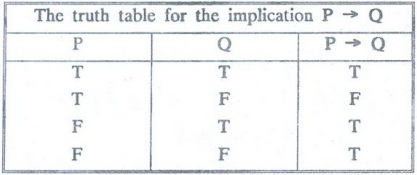
Conditional Statement: [If, ... then] [→]

If P and Q are any two statements, then the statement P→ Q which is read as "If P, then Q" is called a conditional statement.

The statement P→ Q has a truth value F when Q has the truth value F and P the truth value T, otherwise it has the truth value T.

Note :

1. In this implication P is called the hypothesis (or antecedent or premise) and Q is called the conclusion (or consequence).

2. It is not necessary that there by any kind of relation between P and Q in order to form P→ Q.

Table 4

Example 1: P : I am hungry [True]

Q : I will eat [True]

P -> Q : If I am hungry, then I will eat. [True]

Example 2: P : The sun is shining today. [True]

Q : 2+8 = 6 [False]

P -> q : If the sun is shining today, then 2 + 8 = 6 [False]

Example 3: P : 2+5 = 8 [False]

Q : 7+3 = 9 [False]

P -> q: If 2 + 5 = 8, then 7+ 3 = 9 [True]

Example 4: P : I do not get the money. [False]

Q: I shall buy the car. [True]

P -> q: If I do not get the money, then I shall buy the car. [True]

Biconditional [equivalence] statement [<->] [if and only if]

If P and Q are any two statements, then the statement P <-> Q, which is read as, "P if and only if Q" and abbreviated as "P iff Q", is called a biconditional statement.

The statement P <-> Q has the truth value T whenever both P and Q have identical truth values.

Table 5

Note: P <-> Q has exactly the same truth value as (P→Q)^(Q→P).

Example 1: P : You can take the flight. [True]

Q: You buy a ticket. [True]

P<->Q: You can take the flight if and only if you buy

a ticket. [True]

Example 2: P : You cannot take the flight. [False]

Q: You do not buy a ticket. [False]

P<->Q: You cannot take the flight if and only if you do not buy a ticket. [True]

Example 3: P : 3 > 2 [True]

Q : 0 < 3-2 [True]

P<->Q : 3 > 2 if and only if 0 < 3-2

Example 4: P : 5 < 6 [True]

Q :7> 8 [False]

P<->Q : 5 < 6 if and only if 7 > 8 [False]

Example 5: P : 2 > 3 [False]

Q : 4 < 5 [True]

P<->Q : 2 > 3 if and only if 4 < 5 [False]

Exclusive or of P and Q [P ⊕ Q]

Let P and Q be propositions. The exclusive or of P and Q, denoted by P⊕Q, is the proposition that is true when exactly one of P and Q is true and is false otherwise.

Table 6

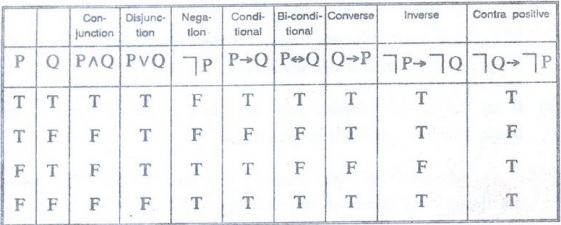
Converse, Contrapositive, Inverse

1. The proposition Q → P is called the converse of P→ Q

2. The proposition ┐Q → ┐P is called the contrapositive of P→ Q

3. The proposition ┐P →  ┐Q is called the inverse of P → Q.

Contrapositive

If P→ Q is an implication, then the converse of P→ Q is the implication Q→ P, and the contrapositive of P→ Q is the implication ┐Q → ┐P.

Example 1: Give the converse and the contrapositive of the implication "If it is raining, then I get wet". [A.U. April/May, 2004]

Solution : P: It is raining.

Q: I get wet.

Q→ P: (converse) If I get wet, then it is raining.

┐Q→ ┐P: (contrapositive) If I do not get wet, then it is not raining.

Example 2: Consider the following conditional statement.

P: "If the flood destroys my house or the fire destroys my house, then my insurance company will pay me".

(a) Which of the following is the converse of P ?

(b) Which of the following is the contrapositive P ?

(i) If my insurance company pays me, then the flood destroys my house or the fire destroys my house.

(ii) If my insurance company pays me, then the flood destroys my house and the fire destroys my house.

(iii) If my insurance company does not pay me, then the flood does not destroy my house or the fire does not destroy my house.

(iv) if my insurance company does not pay me, then the flood does not destroy my house and the fire does not destroy my house. [Ans. (a) (i), (b) (iii)]

Example 3:  State the converse, contrapositive, and inverse of "A positive integer is a prime only if has no divisors other than 1 and itself".

Solution :

(i) Converse: "A positive integer is a prime if it has no divisors other than 1 and itself."

(ii) Contrapositive: "If a positive integer has a divisor other than 1 and itself, then it is not prime".

(iii) Inverse: "If a poisitive integer is not prime, then it has a divisor other than 1 and itself".

Example 4. State the converse, contrapositive, and inverse of "If it snows today. I will ski tomorrow".

Solution :

(i) Converse: "I will ski tomorrow only if it snows to-day".

(ii) Contrapositive: "If I do not ski tomorrow, then it will not have snowed today".

(iii) Inverse: "If it does not snow today, then I will not ski tomorrow".

Table-7

Well-formed Formulas

1. A well-formed formula can be generated by the following rules:

1. A statement variable standing alone is a well-formed formula.

2. If A is a well-formed formula, then A is a well-formed formula.

3. If A and B are well-formed formulas, then (A^B), (A˅B), (A→B), and (A ↔ B) are well-formed formulas.

4. A string of symbols containing the statement variables, connectives, and parenthesis is a well-formed formula, iff it can be obtained by finitely many applications of the rules 1, 2 and 3.

2. According to this definition, the following are well-formed formulas.

1. ┐ (P Ʌ Q)

2. ┐ (P ˅ Q)

3. (P → (P ˅ Q))

4. (P → (Q → R))

5. (((P → Q) ^ (Q → R)) ↔ (P → R))

3. The following are not well-formed formulas.

1. ┐P˄Q correct form is (P˄ Q) or (P˄ Q)

2. (P→ Q) → (˄ Q). This is not a wff because ˄ is Q is not

3. (P → Q. correct form is (P → Q)

4. (PA Q) → Q) correct form is ((PA Q) → Q)

Note: For the sake of convenience we shall omit the outer parenthesis. Thus we write P˄Q in the place of (P˄Q)

 (P˄Q) → Q in the place of ((P ^ Q) → Q)

Precedence of Logical Operators

We can construct compound propositions using the negation operator and the logical operators defined so far. We will generally use parenthesis to specify the order in which logical operators in a compound proposition are to be applied.

Table 8

Translating English Sentences

There are many reasons to translate English sentences into expressions involving propositional variables and logical connectives. In particular, English is often ambiguous. Translating sentences into logical expressions removes the ambiguity. Moreover, once we have translated sentences from English into logical expressions we can analyze these logical expressions to determine their truth values, we can manipulate them, and we can use rules of inference to reason about them.

Example 1: How can this English sentence be translated into a logical expression? [MCA A/M 2003]

"You can access the Internet from campus only if you are a computer science major or you are not a freshman".

a: You can access the Internet from campus.

b: You are a computer science major.

c: You are a freshman.

┐c: You are not a freshman.

a → (bv ┐c)

Note : only if represents the symbol →

or represents the symbol ˅

not represents the symbol ˄

Example 2: Write the following statement in symbolic form. If either Ram takes calculus or Krishna takes sociology, then Sita will take English.

a: Ram takes calculus.

b: Krishna takes sociology.

c: Sita takes English.

(a v b) → c

Example 3: State the truth value of "If tigers have wings then the earth travels round the sun". [A.U. A/M, 2003]

Solution: Let

P: Tigers have wings "F"

Q: The earth travels round the sun "F"

The given statement is P → Q, has the truth value "T"

Boolean searches :

In Boolean searches, the connective AND is used to match both of two search terms, the connective OR is used to match one or both of two search terms, and the connective NOT is used to exclude a particular search term.

Logic Puzzels :

Using logical reasoning puzzles can be solved are known as logic puzzles.

Example 4: Write the following statement in symbolic form

"You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old".

Solution: Let

a: You can ride the roller coaster

b: You are under 4 feet tall

c: You are older than 16 years old.

Then the sentence can be translated to

(b˄┐c) → a

Example 5: Let p and q be the propositions "Swimming at the Chennai shore is allowed" and "Sharks have been spotted near the shore", respectively. Express each of these compound propositions as an English sentence.

(a) ┐ q

(b) ┐p v q

(c) p ^ q

(d) 7 q → p

(e) p → ┐q

(f) ┐P ^ (P V ┐q)

Solution :

(a) Sharks have not been spotted near the shore

(b) Swimming at the Chennai shore is not allowed, or sharks have been spotted near the shore.

(c) Swimming at the Chennai shore is allowed, and sharks have been spotted near the shore.

(d) If sharks have not been spotted near the shore, then swimming at the Chennai shore is allowed.

(e) If swimming at the Chennai shore is allowed, then sharks have not been spotted near the shore.

(f) Swimming at the Chennai shore is not allowed, and either swimming at the Chennai shore is allowed or sharks have not been spotted near the shore.

Example 6: Let Р and q be the propositions

p: It is below freezing.

q: It is snowing

Write the following statements in symbolic form.

(i) It is below freezing but not snowing.

(ii) It is below freezing and snowing.

(iii) It is either snowing or below freezing (or both)

(iv) It is not below freezing and it is not snowing

(v) It is either below freezing or it is snowing, but it is not snowing if it is below freezing.

(vi) If it is below freezing, it is also snowing.

(vii) That it is below freezing is necessary and sufficient for it to be snowing.

Solution :

(i) р Ʌ ┐q

(ii) p Ʌ q

(iii) p v q

(iv) ┐p Ʌ ┐q

(v) (p v q) ^ (p → ┐q)

(vi) p → q

(vii) q ↔ p

Example 7: Let p, q and r be the propositions

p: Bears have been seen in the area

q: Hiking is safe on the trial.

r: Berries are ripe along the trial.

Write these propositions using p, q and r and logical connectives.

(i) Bears have not been seen in the area and hiking on the trial is safe, but berries are ripe along the trail.

 (ii) If berries are ripe along the trial, hiking is safe if and only if bears have not been seen in the area.

(iii) It is not safe to hike on the trial, but bears have not been seen in the area and the berries along the trial are ripe.

(iv) Hiking is not safe on the trial whenever bears have been seen in the area and berries are ripe along the trail.

(v) For hiking on the trial to be safe, it is necessary but not sufficient that berries not be ripe along the trial and for bears not to have been seen in the area. Ʌ ┐

Solution: (i) ┐p Ʌ q Ʌ r

(ii) r→ (q ↔ ┐p)

(iii) ┐qɅ ┐p Ʌ г

(iv) (p Ʌ r) → ┐ q

(v) (q→ (┐ṛ^ ┐p)) ^ ┐((┐r^ ┐p) → q)

Example 8: Write each of these statements in the form "if p then q" in English.

(a) It snows whenever the wind blows from the north-east

(b) The apple trees will bloom if it stays warm for a week.

(c) If you drive more than 500 miles, you will need to buy gasoline.

(d) Your guarantee is good only you bought your CD player less than 80 days ago.

Solution :

(a) If the wind blows from the north east, then it snows.

(b) If it stays warm for a week, then the apple tree will bloom.

(c) If you drive more than 500 miles, then you will need to by gasoline.

(d) If your guarantee is good, then you must have bought your CD player less than 80 days ago.

Logic and Bit Operations

Computers represent information using bits.

A bit has two possible values, namely 0 (zero) and 1 (one). We will use a 1 bit to represent true and a 0 bit to represent false. That is, 1 represents T, 0 represents F.

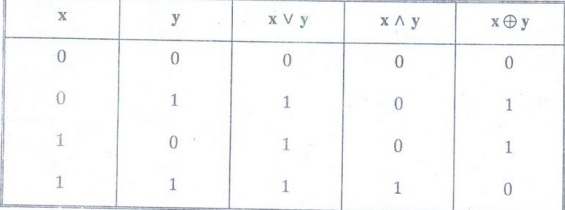
Table 9

We will use the notation OR, AND, and XOR for the operators V, A and⊕

Table 10

Definition :

A bit string is a sequence of zero or more bits. The length of this string is the number of bits in the string.

Example (1) 11 1011 1111 is a bit string of longer ten.

Example (2) Find the bitwise OR, bitwise AND and bitwise XOR of the bit strings 01 1011 0110 and 11 0001, 1101

Example 3: Find the bitise OR, bitwise AND, and bitwise XOR of the bit strings 11 1111 1111, 00 0000 0000

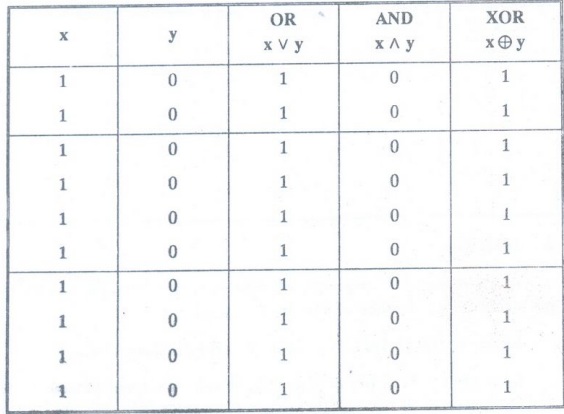
i.e., Bitwise

OR is 11 1111 1111

AND is 00 0000 0000

XOR is 11 1111 1111

TRUTH TABLE

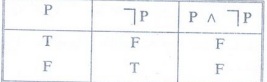
Example 1: Construct the truth table for P˄┐P

Solution :

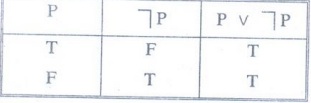
Example 2: Construct the truth table for P c ┐P

Solution :

Example 3 : Construct the truth table for P ˄ P.

Solution :

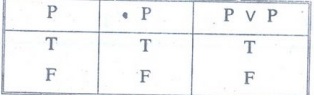
Example 4: Construct the truth table for PV P

Solution :

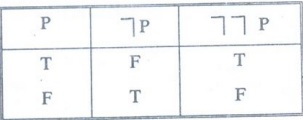
Example 5: Construct the truth table for ┐┐P

Solution :

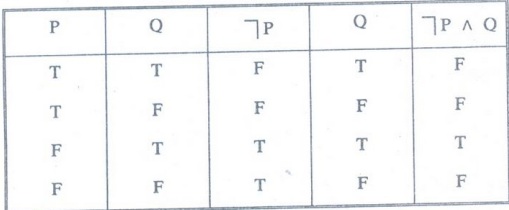
Example 6: Construct the truth table for ┐P˄Q

Solution: Since there are two variables, therefore there are 2² possible truth values.

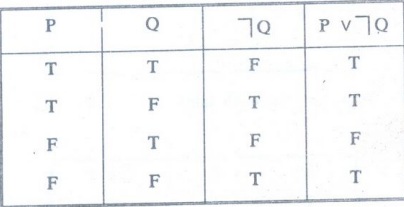
Example 7: Construct the truth table for PV ┐Q [MCA 1995, M.U]

Solution :

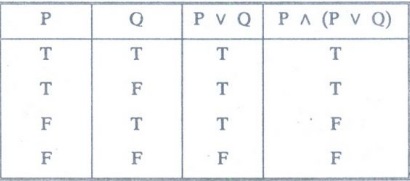
Example 8: Construct the truth table for P˄ (P v Q) [M.C.A] [M.U. 94]

Solution :

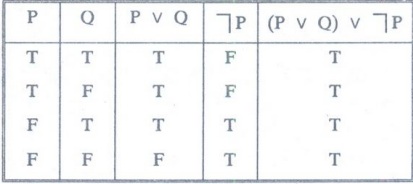
Example 9: Construct the truth table for (P v Q) v ┐P [M.C.A] [M.U.94]

Solution :

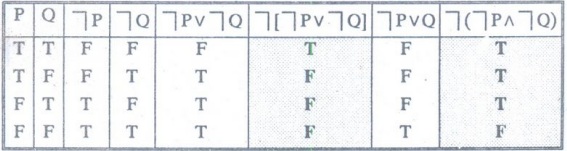
Example 10 : Construct the truth table for the following:

(a) ┐ (┐P v ┐Q)

(b) ┐ (┐р ˄┐Q)[M.C.A, 95, M.U]

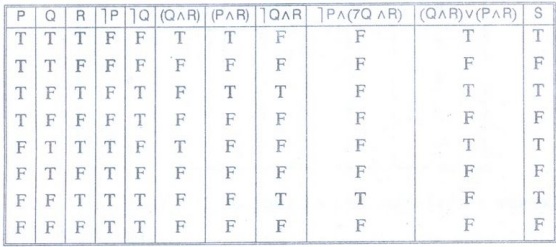
Example 11: (┐P^ (┐Q^ R)) V ((Q ^ R) V (P ^ R)) [A.U A/M 2003]

Sol. Let S = (┐p ^ (┐Q^ R)) V ((Q ^R) V (P^R))

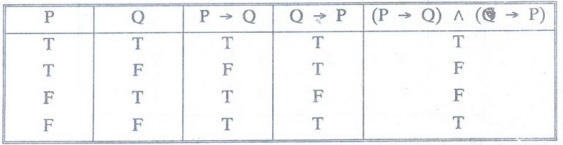
Example 12: Construct the truth table for (P -> Q) Ʌ (Q→ P) [1991, MCA, M.U]

Solution :

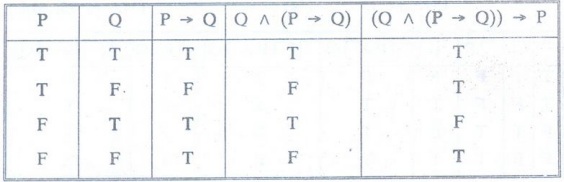
Example 13: Construct the truth table for (Q^ (P → Q)) -> P [MCA, 93, M.U]

Solution :

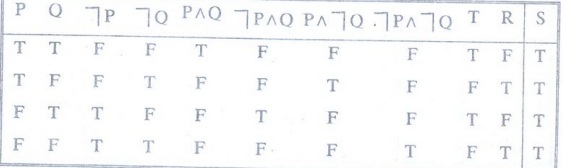
Example 14: Construct the truth table for

(P^Q) V (┐P^Q) v (P^┐Q) V (┐P^┐Q) [MCA 96, MU]

Solution: Let S = (P^Q) V (┐P^Q) V (P ^ ┐Q) v. (┐P^┐Q)

R = (P ^ ┐Q) v. (┐P^┐Q)

T = (P^Q) V (┐P^Q)

Example 15: Construct the truth table for ┐(P^Q) ↔ (┐P V┐Q) [MCA, MU 1990]

Solution :

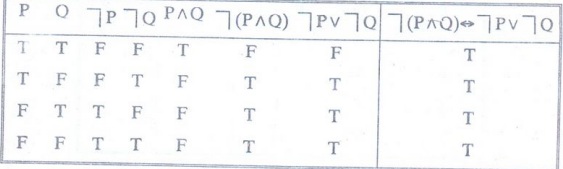
Example 16: Construct the truth table for (P → Q) ↔ (P v Q)

Solution :

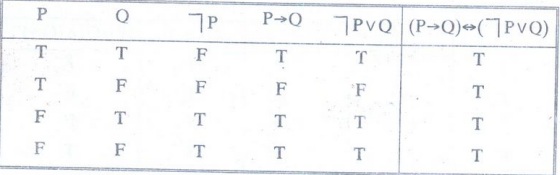
Example 17: Construct the truth table for ┐ (P v Q) ^ (PVR)

Solution :

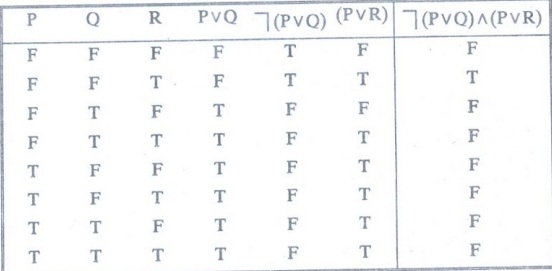
Example 18: Construct the truth table for (P →Q) → P

Solution :

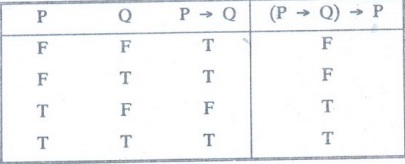
Example 19: Construct the truth table for the statement formula.

(P→Q) ^ (Q→ P) [MCA 1991, MU]

Solution :

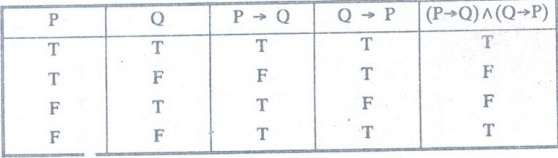
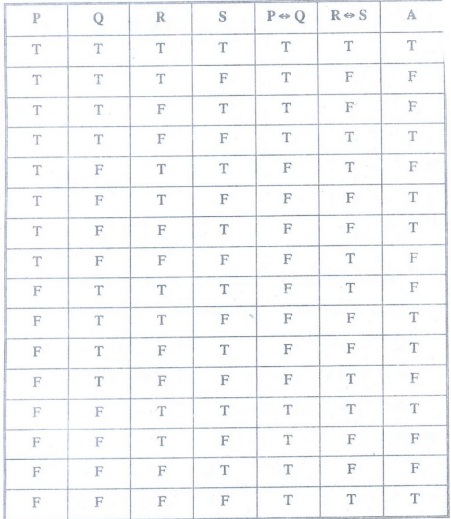
Example 20: Construct a truth table for (P ↔ Q) ↔ (R ↔ S)

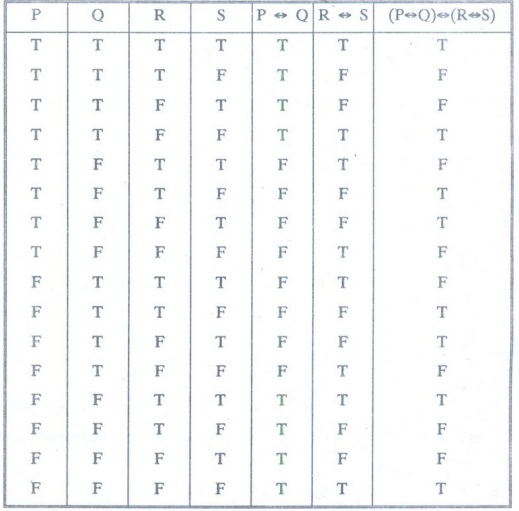
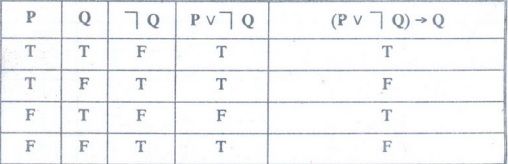
Example 21 : Construct the truth table for (P V ┐ Q) → Q

Solution :

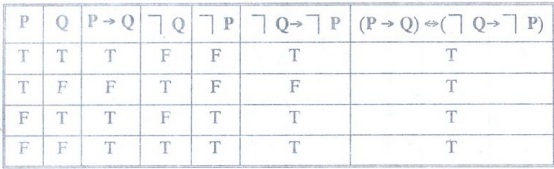
Example 22 : Construct the truth table for (P→ Q) ↔ (┐ Q→ ┐ P)

Solution :

Example 23 : Construct the truth table for (P→ Q) → (Q→ P)

Solution :

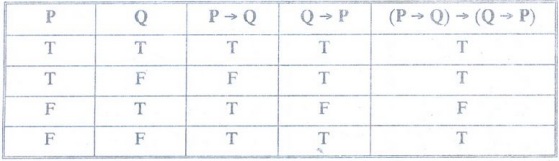
Example 24 : Construct the truth table for the following compound

propositions.

(a) (P v Q) → (P⊕Q )

(b) (P⊕Q) → (P^Q).

(c) (P ↔ Q) ⊕ ->(┐P ↔ Q)

(d) (P v Q) ⊕ (P^Q)

(e) (P⊕Q) → (P⊕ ┐Q)

Solution :

Example 25: Construct the truth table for (P → Q) ⊕  (┐P ↔ ┐R)

Solution :

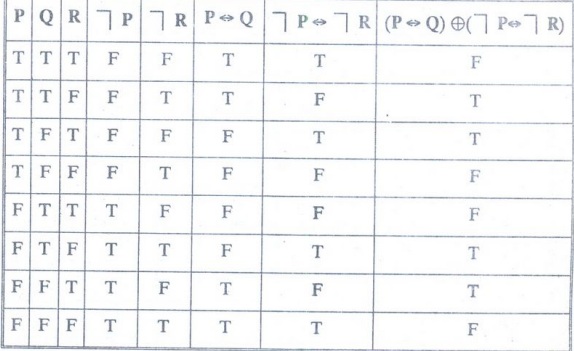
Example 26: Construct the truth table for

(a) P→ ┐Q

(b) ┐ P ↔ Q

(c) (P→ Q) v (┐P→ Q)

(d) (P ↔ Q) V (┐P ↔ Q)

 (e) (┐P ↔ ┐Q) ↔ (P ↔ Q)

Solution :

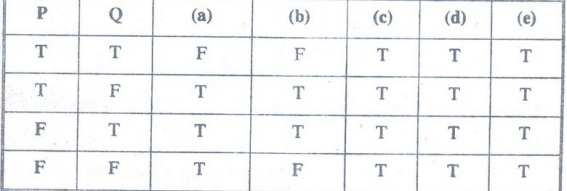
Example 27: Construct a truth table for (P ↔ Q) ↔ (R ↔ S)

Solution: Let A = (P ↔ Q) ↔ (R ↔ S)

Example 28 : Construct a truth table for each of these compound propositions.

(a) P→ (┐QVR)

(b) (P→Q) ^(┐P→R)

(c) (P ↔ Q) v(┐Q ↔ R)

(d) (┐P ↔ ┐Q) ↔ (Q ↔ R)

Solution :

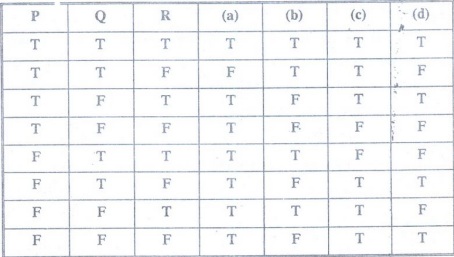
EXERCISE

1. What is the negation of each of the following propositions.

 (a) Today is thursday.

(b) There is no pollution in New Delhi.

(c) 3 + 1= 4

(d) The summer in Chennai is hot and sunny.

Ans.

(a) Today is not Thursday.

(b) There is pollution in New Delhi.

(c) 3+1≠ 4.

(d) The sumer in Chennai is not hot or it is not sunny.

2. Determine whether each of the following implications is true or false.

 (a) if 1 + 1= 2, then 2 + 2 = 5 Ans.F

(b) if 1 + 1 = 3, then 2 + 2 = 4 Ans.T

(c) if 1 + 1 = 3, then 2 + 2 = 5 Ans.T

(d) if pigs can fly then 1 + 1 = 3 Ans.T

(e) if 1 + 1 =3, then god exists Ans.T

3. Write the statement "the crop will be destroyed if there is a flood" in symbolic form.

Ans.

P: crop will be destroyed.

Q: There is a flood.

Q→ P

4. Construct the truth table for the following propositions.

(a) Р^ ┐Q

(b) P v ┐Q

(c) (P v ┐Q) → Q

(d) (P vQ) → (P^Q)

(e) (P→Q) <->(┐Q →┐P)

(f) (P→Q)→(Q→P)

(g) (P→Q) ^ (┐P→R)

(h) (┐P <->┐0) <-> (P<-> Q)